
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Однородные и неоднородные системы линейных алгебраических
Уравнений
Определение. Система Л.А.У., все свободные члены которой нулевые, называется однородной. Система, столбец свободных членов которой ненулевой, называется неоднородной. В общем случае однородная система из m уравнений с n неизвестными имеет вид:
В матричной форме она записывается в виде AX=0. Здесь Однородная система всегда совместна, так как она имеет решение x1=0, x2=0,..., xn=0, которое называется тривиальным. Матричный метод и метод Крамера не имеет смысла применять для решения однородных систем с квадратной матрицей A. Поскольку, если A не вырождена, то система имеет единственное тривиальной решение, если же |A| =0, то эти методы неприменимы, система имеет бесконечное число решений. Метод Гаусса для решения однородных систем используется в следующем виде. Записываем матрицу системы A и с помощью элементарных преобразований приводим её к верхнетреугольному виду. Возможны два случая. 1) r (A)=n. Система имеет единственное тривиальное решение. Пример 1.
Запишем матрицу системы и преобразуем её.
r (A)=3, следовательно, система имеет единственное решение:
2) r (A)<n. Система имеет бесконечно много решений, зависящих от n–r параметров. Пример 2.
Преобразуем матрицу системы.
r (A)=2, поэтому система имеет бесконечно много решений, зависящих от одного параметра. Восстановим систему и решим её.
Обозначим решение системы (1) 1. Если строка 2.Если строка Из сформулированных свойств следует, что всякая линейная комбинация решений системы линейных однородных уравнений также является решением этой системы. Поэтому представляет интерес найти такие линейно независимые решения системы (1), через которые линейно выражались бы все остальные ее решения. Определение. Система линейно независимых решений Теорема. Если ранг r матрицы коэффициентов при неизвестных системы линейных однородных уравнений (1) меньше числа неизвестных n, то всякая фундаментальная система решений системы (1) состоит из n-r решений.
Поэтому общее решение системы (1) линейных однородных уравнений имеет вид:
Где
Пример3. В последнем рассмотренном примере
мы получили, что r (A)=2, поэтому фундаментальная система решений состоит из 3–2=1 решения. Чтобы его получить, положим в общем решении системы Контрольные вопросы
Литературы: Основная [1] § 1,2,3,4 стр. 5-33 [6] § 1,3 стр. 12-42, стр. 66-83 [19] Глава 1.8- 1.12, 1.14 стр. 52-58, 72-83, 87-94 Дополнительная [30] § 2.4.4, стр. 151-168
|
|||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.19.31.73 (0.008 с.) |
 (1)
(1)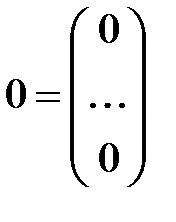 – нулевой столбец.
– нулевой столбец.


 ~
~ 
 ~
~ 
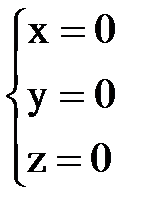
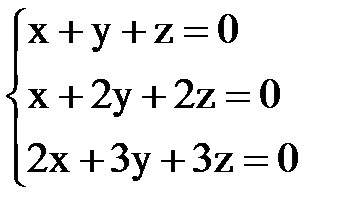




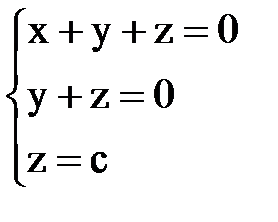


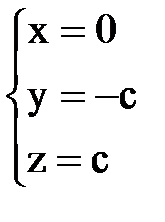
 в виде строки
в виде строки 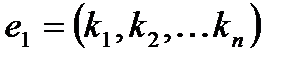 . Решения системы линейных однородных уравнений обладают следующими свойствами:
. Решения системы линейных однородных уравнений обладают следующими свойствами: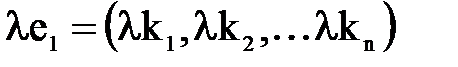 - также решение этой системы.
- также решение этой системы. - решения системы (1), то при любых
- решения системы (1), то при любых 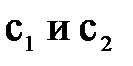 их линейная комбинация
их линейная комбинация  - также решение данной системы.
- также решение данной системы. называется фундаментальной, если каждое решение системы (1) является линейной комбинацией решений
называется фундаментальной, если каждое решение системы (1) является линейной комбинацией решений  .
.
 - любая фундаметальная система решений,
- любая фундаметальная система решений, - произвольные числа и
- произвольные числа и  .
.
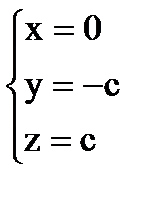 или
или  . Пусть c =1, следовательно,
. Пусть c =1, следовательно,  и любое решение системы имеет вид линейной комбинации:
и любое решение системы имеет вид линейной комбинации:  .
.


