
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоретические основы расчета свайного фундаментаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Как стержневой системы
Методика расчета свайного фундамента основана на решении задачи о деформировании сваи в грунтовой среде под действием нагрузок, приложенных в уровне поверхности грунта. Рассмотрим случай, когда внешние нагрузки лежат в одной плоскости. Представляя сваю в виде упругого стержня для него записывают дифференциальное уравнение изогнутой оси [4]:
Изгиб сваи обусловлен действием поперечной силы
где Параметры Уравнение (4.17) записывается в виде:
Параметр
Решение уравнения (4.19) было дано И.В.Урбаном и предназначалось для расчета шпунтовой стенки в условиях плоской деформации. Заметим, что при изгибе упругого стержня справедливы следующие зависимости:
Решение И.В.Урбана с учетом приведенных выражений (4.21) дает следующую систему уравнений, определяющую работу сваи в грунте [4]:
Коэффициенты приведенных уравнений определяются бесконечными рядами в зависимости от приведенной глубины рассматриваемой точки
Таким образом, система уравнений (4.23) позволяет определить горизонтальное перемещение сваи Заметим, что при расчете свайного фундамента с низким ростверком глубина Как правило, исходными данными для расчета деформаций сваи являются нагрузки
Перемещения сваи в уровне поверхности грунта от единичных усилий -
Для определения коэффициентов 1). для висячей сваи в уровне ее нижнего конца принимают равными нулю внутренние усилия:
2). при опирании сваи на скалу (свая-стойка):
3). при заделки сваи-стойки в скалу:
Далее, рассмотрим сваю, имеющую свободную длину, и нагруженную поперечной силой
Перемещения сваи в уровне верхнего сечения от единичных усилий -
Таким образом, приведенные в этом параграфе выражения позволяют рассчитать деформирование одиночной сваи в грунте, представленном упругой средой, описываемой с помощью гипотезы коэффициента постели, от действия горизонтальной и моментной нагрузок.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.252.226 (0.01 с.) |

 (4.17)
(4.17) и момента
и момента 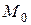 приложенных в уровне поверхности грунта. Нагрузка
приложенных в уровне поверхности грунта. Нагрузка  характеризует горизонтальный отпор грунта и определяется согласно гипотезе коэффициента постели:
характеризует горизонтальный отпор грунта и определяется согласно гипотезе коэффициента постели: (4.18)
(4.18) - коэффициент условия работ;
- коэффициент условия работ; 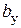 - условная ширина сваи.
- условная ширина сваи. м при диаметрах сваи
м при диаметрах сваи  0,8 м, и
0,8 м, и 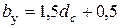 м для меньших диаметров. Коэффициент условия работ принимается равным
м для меньших диаметров. Коэффициент условия работ принимается равным  при специальном учете пластического разрушения грунта около сваи, и
при специальном учете пластического разрушения грунта около сваи, и  , если это явление не учитывается. Указанные значения
, если это явление не учитывается. Указанные значения  (4.19)
(4.19) называется коэффициентом деформации сваи и рассчитывается по формуле:
называется коэффициентом деформации сваи и рассчитывается по формуле: (4.20)
(4.20) ;
; 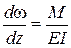 ;
;  (4.21)
(4.21)
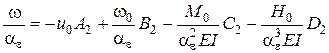


 [4]:
[4]:
 »
»1 -
»
»1 -  (1-
(1- 
 +
+  »
»
»
» 

 »
»
»
» 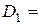

 »
»
»
» 



 , поворот ее сечения
, поворот ее сечения  , а также внутренние усилия - изгибающий момент
, а также внутренние усилия - изгибающий момент  и поперечную силу
и поперечную силу  в сечении на произвольной глубине
в сечении на произвольной глубине  , если известны значения данных параметров в уровне поверхности грунта:
, если известны значения данных параметров в уровне поверхности грунта:  ,
,  и
и  .
.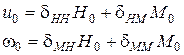 (4.24)
(4.24) (рис. 4.30) даются выражениями:
(рис. 4.30) даются выражениями: (4.25)
(4.25) Рис. 4.30. Перемещения сваи в уровне поверхности грунта
от единичных усилий
Рис. 4.30. Перемещения сваи в уровне поверхности грунта
от единичных усилий
 ,
,  и
и 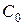 принимаются следующие граничные условия [4]:
принимаются следующие граничные условия [4]:
 и
и  . Индекс «
. Индекс «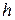 » здесь будет означать, что рассматриваемая величина определяется для глубины
» здесь будет означать, что рассматриваемая величина определяется для глубины 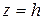 . Далее, из третьего и четвертого уравнений системы (4.22) получаются следующие выражения для искомых коэффициентов:
. Далее, из третьего и четвертого уравнений системы (4.22) получаются следующие выражения для искомых коэффициентов: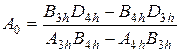
 (4.26)
(4.26)
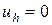 ,
, 
 (4.27)
(4.27)
 0. Первое и второе уравнения системы (4.22) приводят к выражениям:
0. Первое и второе уравнения системы (4.22) приводят к выражениям:
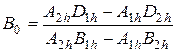 (4.28)
(4.28)
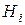 и моментом
и моментом 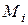 в уровне верхнего сечения. Запишем выражения для перемещений
в уровне верхнего сечения. Запишем выражения для перемещений  и
и 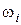 этого сечения:
этого сечения:
 (рис. 4.31) определяются с помощью решений (4.24) и решения строительной механики об изгибе консоли:
(рис. 4.31) определяются с помощью решений (4.24) и решения строительной механики об изгибе консоли:
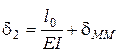 (4.30)
(4.30)
 Рис. 4.31 Перемещения сваи в уровне подошвы плиты ростверка
от единичных усилий
Рис. 4.31 Перемещения сваи в уровне подошвы плиты ростверка
от единичных усилий



