
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет прочности фундаментовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В жестких фундаментах, очертание которых не выходит за угол жесткости их кладки a = 30°, растягивающие напряжения от изгиба в уступах практически отсутствуют, а сжимающие напряжения существенно меньше сопротивления материала кладки сжатию и потому не требуют проверки расчетом. В конструкциях гибких фундаментов возникают значительные изгибающие моменты и расчет их прочности становится необходимым. В таких расчетах часто используют схему линейного распределения давлений по подошве фундаментов. От этих давлений определяют изгибающие моменты и поперечные силы в сечениях той или иной фундаментной конструкции. Так, например, при внецентренном загружении внешней нагрузкой вытянутого в плане фундамента расчетные усилия в сечении его консольного выступа (рис.3.9, а) на 1 м длины вычисляют по формулам: M = С 2(2 p max + pc)/6, Q = C (p max + pc)/2, (3.33) где C - ширина консольного выступа; p max и pc - соответствующие давления от расчетных внешних нагрузок (формула (3.5)), передаваемые на грунт под краем фундамента в расчетном сечении. Изгибающие моменты в расчетных сечениях фундаментной плиты под отдельную колонну с размерами подошвы l и b (рис. 3.9, б) вычисляют по формулам: в направлении l (большего размера подошвы)
в направлении b (меньшего размера подошвы)
Поперечная сила в сечении Q = Ci (p max + pc)/2. (3.35)
По найденным значениям расчетных усилий M и Q проверяют прочность материала в сечениях фундамента, назначают армирование железобетонных фундаментных конструкций и проверяют их трещиностойкость. Отметим, что фундаментные плиты под отдельные колонны, кроме расчета на изгиб, проверяют еще на продавливание, которое предполагается по поверхности пирамиды, грани которой наклонены к вертикали под углом 45°(см. рис. 3.9, б). Проверку выполняют по формуле F £ Rbthobo, (3.36) где F = Ao p max - расчетная продавливающая сила (Ao — площадь многоугольника abcdeg); Rbt — расчетное сопротивление бетона растяжению; ho - высота сечения (от верха плиты до оси продольной арматуры); bo - среднеарифметическое значение верхнего и нижнего размеров грани пирамиды продавливания.
Для гибких фундаментных блоков и плит, нагруженных группами стоек или столбов, а также для сплошных плит под сооружением допущение о линейном распределении реактивных давлений по подошве может иногда привести к значительным ошибкам в определении размеров сечения и армировании фундаментов. Для таких фундаментов эпюры реактивных давлений грунта на подошву следует уточнять по теории расчета балок и плит на деформируемом основании. Существует две группы методов расчета гибких балок и плит на деформируемом основании. В методах первой группы используется гипотеза коэффициента постели Фусса-Винклера (Н.П. Пузыревский, А.Н. Крылов и др.), согласно которой осадки грунта в некоторой точке зависят только от давления в этой точке и не зависят от давлений, действующих по соседству, что не соответствует действительной распределительной способности грунта. Однако решения при использовании этой гипотезы получаются довольно простыми, а результаты расчетов во многих случаях оказываются достаточно близкими к таковым, полученным более строгими методами. Гипотезу коэффициента постели используют для расчета сложных конструкций гибких фундаментов. Вторая группа методов базируется на гипотезе упругого полупространства, учитывающей распределительную способность грунта в рамках линейной теории его деформирования по закону Гука. Для практических расчетов наиболее удобен и универсален метод В.Н. Жемочкина. Он применим как для расчета полос в условиях плоской задачи, так и для расчета балок в условиях пространственных задач. На рис. 3.10 показана расчетная схема балки на упругом полупространстве по методу В.Н. Жемочкина. Здесь неизвестными в расчете являются силы Fi в опорных стержнях, вертикальные перемещения si и угол поворота a i в каком-либо сечении, принятом за начальное. Горизонтальный стержень поставлен для придания системе статической неизменчивости и никакой роли в расчетах не играет. Такая система соответствует смешанному методу расчета статически неопределимых стержневых систем. Для определения неизвестных этой системы составляют, во-первых, контактные уравнения совместности прогибов балки и осадок грунта в точках постановки опорных стержней. К контактным уравнениям добавляют два обычных уравнения статики, вытекающих из условия равновесия сил.
После решения системы исходных линейных уравнений и нахождения неизвестных Fi нетрудно по правилам статики найти изгибающие моменты и поперечные силы в любых сечениях фундамента. Для расчета балок и плит на упругом полупространстве широко используются также табулированные решения М.И. Горбунова-Посадова и И.А. Симвулиди [3].
|
|||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.66.85 (0.01 с.) |

 ;
; , (3.34)
, (3.34)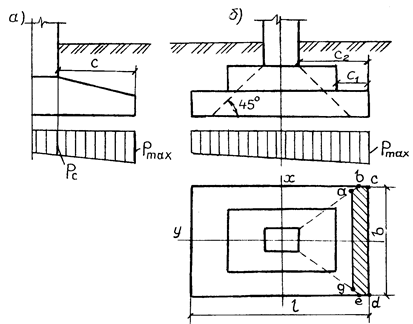 Рис. 3.9.Расчетные схемы прочности гибких фундаментов
при линейном распределении давлений на грунт
Рис. 3.9.Расчетные схемы прочности гибких фундаментов
при линейном распределении давлений на грунт



