
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет количества вещества чистой жидкостиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если известна масса, то расчет аналогичен расчету для индивидуального твердого вещества. Если известен объем жидкости, то 1 Найти массу этого объема жидкости: mж = Vж·ρж, где mж – масса жидкости г; Vж – объем жидкости, мл; ρж – плотность жидкости, г/мл.
2 Найти число молей жидкости:
Эта методика подходит для любого агрегатного состояния вещества. Пример: Определить количества вещества Н2О в 200 мл воды. Решение: если температура не оговаривается, то плотность воды принимается 1 г/мл, тогда:
1 2
Расчет количества растворенного вещества в растворе, Если известна его концентрация Если известна массовая доля растворенного вещества, плотность раствора и его объем, то 1 Рассчитать массу раствора: mр-ра = Vр-ра·ρр-ра, где mр-ра – масса раствора, г; Vр-ра – объем раствора, мл; ρр-ра – плотность раствора, г/мл. 2 Рассчитать массу растворенного вещества
где
3 Рассчитать число молей растворенного вещества
Пример: Определить количество вещества азотной кислоты в 500 мл 10 % раствора кислоты плотностью 1,0543 г/мл. 1 Определить массу раствора mр-ра = Vр-ра·ρр-ра = 500·1,0543 = 527,150 г. 2 Определить массу чистой HNO3
3 Определить число молей HNO3
Если известна молярная концентрация растворенного вещества и вещества и объем раствора, то
где
Расчет количества индивидуального Если дана масса газообразного вещества, то Если дан объем, измеренный при нормальных условиях, - то по формуле (2), если объем газообразного вещества измерен при любых других условиях, - то по формуле (3),формулы приведены на страницах 6-7.
Газовые смеси Газовые смеси всегда однородны (гомогенны). Каждый компонент газовой смеси имеет свой парциальный объем (Vi) и парциальное давление (Рi). Парциальным называют давление компонента газовой смеси, если бы компонент занимал весь объем газовой смеси, а другие компоненты отсутствовали. Парциальным объемом называют объем, который занимал бы компонент газовой смеси, если его давление было равно давлению в газовой смеси, а другие компоненты отсутствовали. Согласно закону Дальтона Рсмеси = Σ Рi; Vсмеси = Σ Vi. Состав газообразной смеси чаще всего выражается в объемных или мольных долях. Объемная доля (φi) – есть отношение парциального объема компонента к общему объему газовой смеси, а мольная доля (χi) – отношение количества вещества компонента к общему количеству вещества смеси:
Объемная и мольная доли могут быть выражены в долях единицы или в процентах. Для газовых смесей значения объемной и мольной доли одного и того же компонента равны. Парциальное давление и объем компонента газовой смеси связаны с общим объемом и давлением следующие соотношениями:
Рi = Рсмеси· φi = Рсмеси· χi Vi = Vсмеси· φi = Vсмеси· χi. Парциальное давление и объем связаны с остальными параметрами газовой смеси через уравнение Менделеева-Клапейрона
Рi Vсмеси = ni R T, Рсмеси·Vi = ni R T. Средняя молярная масса смеси веществ в любом агрегатном состоянии может быть рассчитана из значений мольных долей составляющих компонентов.
Мсмеси = М1· χ1 + М2· χ2 +…+ Мn· χn или Мсмеси = ΣМi· χi, где Мi – молярная масса i-го компонента смеси, г/моль. Для газовых смесей вместо мольных долей можно использовать объемные доли
Мсмеси = ΣМi· φi. Примеры решения задач Пример 1: [1] Смесь оксидов углерода (II) и (IV) массой 48 г занимает объем 33,6 л (при н. у.). Рассчитайте объемы газов в смеси.
Решение: Способ 1 Определить среднюю молярную массу смеси. Можно воспользоваться следствием из закона Авогадро:
Можно рассчитать по уравнению Менделеева-Клапейрона
Определить состав смеси в объемных долях.
Пусть
Следовательно Найти объем каждого компонента газовой смеси
Способ 2 Пусть в смеси содержится х молей СО и y молей СО2. Выразим объем и массу смеси через введенные переменные и составим систему уравнений
Следовательно:
Часто в инженерных расчетах нужно уметь пересчитывать состав газовой смеси из объемных процентов - в массовые, для этого необходимо рассчитать массу смеси и массу каждого компонента в отдельности.
Пример 2: Определить массу 10 м3 газовой смеси состава: 21 % О2 и 79 % N2 при 50 °С и 100 кПа.
Решение: Составы газовых смесей принято рассчитывать в объемных процентах, поэтому можно рассчитывать парциональные объемы кислорода и азота в смеси (
Так как условия отличны от нормальных, то нужно найти количество вещества каждого компонента газовой смеси по формуле (3):
Найдем массу каждого компонента газовой смеси, решив ее относительно mi
Масса газовой смеси равна сумме масс ее компонентов
или
Пример 3: Определить металл, 0,54 г которого вытесняют из щелочи 0,743 л водорода, собранного над водой при температуре 17 °С и давлении 744,53 мм рт. ст. Решение: В задаче не известен металл, а, следовательно, и его степень окисления в соли, поэтому такую задачу удобно решать, используя закон эквивалентов. По закону эквивалентов
где Пользуясь уравнением состояния идеального газа, привести объем водорода к нормальным условиям
где
Для t = 17 °С и
Рассчитать количество вещества эквивалента водорода.
Согласно закону эквивалентов
Найти молярную массу эквивалента металла
С другой стороны
Так как валентность металла неизвестна и в условии задачи не хватает данных для ее расчетного определения, то необходимо определить атомную массу металла путем перебора возможных валентностей. При переборе валентность не может быть более 4, а решением будет металл, который обладает амфотерными свойствами. Перебор удобнее представить в виде таблицы.
Пример 4: Найти элемент, формулу его оксида, состав оксида в массовых долях, показать с помощью реакций его кислотно-основной характер, если известно, что на горение 1,44 г простого вещества израсходовано 0,672 л кислорода, приведенного к н. у.
Решение: В этой задаче также не известен элемент и его степень окисления, но известен второй элемент – кислород, который в большинстве соединений проявляет степень окисления равную (-2), поэтому решать эту задачу удобно, используя закон эквивалентов.
где
следовательно, а
Определить массовые доли элементов в оксиде.
Способ 1 Пусть масса оксида равна m, а массовая доля элемента
Подставить известные и выраженные через х величины
Следовательно, массовая доля кислорода в оксиде 0,4, а массовая доля элемента 0,6.
Способ 2 Найти массу кислорода, прореагировавшего с простым веществом
Масса оксида составит:
Рассчитать массовые доли элементов в оксиде.
Элемент определить аналогично примеру № 3, только для оксидов валентность элемента может быть от 1 до 8 включительно.
Как видно из таблицы задача имеет два решения Mg и Ti. Решение 1 Mg → валентность 2, оксид MgО, свойства – основные, т. е. оксид реагирует с кислотами и не реагирует с щелочами
MgО + 2НСl = MgСl2 + Н2О,
MgО + NaOH ≠
Решение 2 Ti – валентность 4, оксид TiО2, свойства амфотерные, т. е. оксид реагирует как с кислотами, так и с щелочами.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-06; просмотров: 2302; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.171.83 (0.009 с.) |

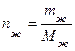 .
.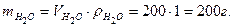
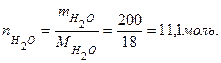
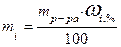 ,
,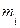 - масса растворенного вещества, г;
- масса растворенного вещества, г; - массовая доля растворенного вещества, выраженная в %.
- массовая доля растворенного вещества, выраженная в %.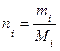 .
.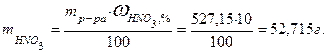
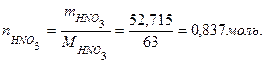
 ,
, - объем раствора, л;
- объем раствора, л;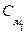 - молярная концентрация i-го вещества в растворе, моль/л.
- молярная концентрация i-го вещества в растворе, моль/л.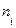 рассчитывается по формуле (1).
рассчитывается по формуле (1).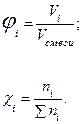
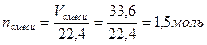 .
.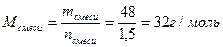 .
.
 .
. .
.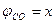 , тогда
, тогда 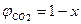 .
. .
.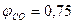 , а
, а  .
.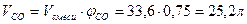 .
. .
.
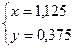
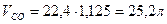
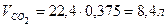
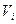 ).
).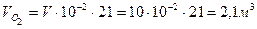 ,
, .
.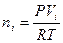 ,
,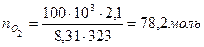 ,
,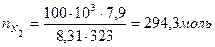 .
.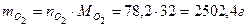 ,
, .
.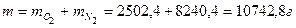
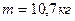 .
.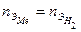 для водорода во всех реакциях
для водорода во всех реакциях  , следовательно,
, следовательно, , но эквивалентный объем водорода изменен при н.у., а в задаче объем газа измерен при t = 17 °С и Ратм = 744,53 мм рт. ст. Кроме этого, в условии задачи сказано, что водород собирали над водой, следовательно, объем вытесненного газа представляет собой газовую смесь Н2 + Н2Опар, поэтому
, но эквивалентный объем водорода изменен при н.у., а в задаче объем газа измерен при t = 17 °С и Ратм = 744,53 мм рт. ст. Кроме этого, в условии задачи сказано, что водород собирали над водой, следовательно, объем вытесненного газа представляет собой газовую смесь Н2 + Н2Опар, поэтому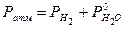 ,
, - давление насыщенного пара воды (см. приложение).
- давление насыщенного пара воды (см. приложение). ,
,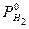 ,
,  ,
, 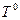 - давление водорода, объем и температура при н. у.
- давление водорода, объем и температура при н. у.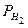 ,
, 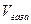 ,
, 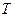 - парциальное давление водорода при температуре Т и в объеме газовой смеси V.
- парциальное давление водорода при температуре Т и в объеме газовой смеси V.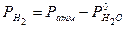 , тогда
, тогда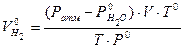 .
.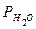 =14,53 мм рт. ст. (см. приложение).
=14,53 мм рт. ст. (см. приложение). .
. .
.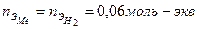 .
.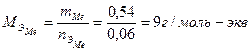 .
.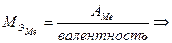
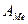 =
=  ·
· 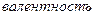 .
. ,
, ,
,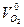 - объем прореагировавшего кислорода при н.у.;
- объем прореагировавшего кислорода при н.у.;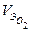 - объем одного моль эквивалента кислорода.
- объем одного моль эквивалента кислорода. ,
,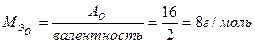 экв.
экв. экв,
экв,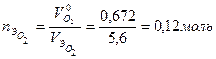 экв.
экв. =
= 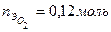 экв,
экв, экв.
экв. , а масса кислорода
, а масса кислорода 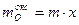 . Согласно следствию из закона эквивалентов
. Согласно следствию из закона эквивалентов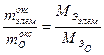 .
. ,
,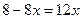 ,
,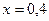 .
.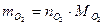 ,
,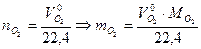
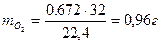 .
.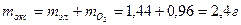 .
.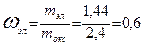 ,
,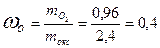 .
.
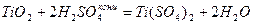 ,
, .
.


