
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основной закон, определяющий величину тока, протекающего через проводник (горную породу) – закон омаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
J = Здесь l – длина проводника в м, S – площадь его поперечного сечения в м2, а ρ – удельное сопротивление, измеряемое в омах, умноженных на метр (ом·м). Величина, обратная ρ называется удельной электрической проводимостью и измеряется в сименсах
Наряду с силой тока, одной из характеристик поля является плотность тока j
Это так называемая дифференциальная форма записи закона Ома, устанавливающая пропорциональность плотности тока в проводнике напряженности поля. Эта форма записи может быть применена к проводникам любой формы и к переменным электромагнитным полям. Поле постоянного электрического тока в однородном полупространстве (ρ = const) называют нормальным электрическим полем постоянного тока. Рассмотрим нормальное поле точечного источника. Получить такое поле, пропуская ток через пару электродов А и В можно, относя второй электрод в бесконечность и анализируя ситуацию в окрестности А. В однородной среде ток от точечного источника стекает во все стороны равномерно. Эквипотенциальные поверхности (поверхности равного потенциала) перпендикулярны к радиальным токовым линиям и имеют форму полусфер с центром в точке А (рис.22)
Рис.22.Нормальное поле одного (а) и двух разнополярных (б) точечных электродов 1 – токовые линии; 2 – эквипотенциальные поверхности.
Определим значение потенциала Uм в точке М. Вначале оценим величину разности потенциалов между двумя близкими эквипотенциальными поверхностями радиусов r и r+dr. Начало координат поместим в точку А. Согласно закону Ома dV=JdR=J Здесь dr – длина проводника - в данном случае расстояние между соседними полусферами, S - это поверхность полусферы, то есть 2πr2, где r – радиус полусферы. Поскольку рассматриваются две полусферы, отстоящие друг от друга на dr – правильнее всего выбрать радиус равным r + dr/2 – то есть выбрать некий «средний» радиус близких полусфер Тогда dV=
Приближенное равенство основано на том, что бесконечно малая dr и при возведении в квадрат и при умножении на конечную величину r дает в результате столь малые «добавки» к r2, что ими вполне можно пренебречь. Для нахождения Uм придется просуммировать согласно определению потенциала все dV от бесконечности до r, то есть проинтегрировать приведенное выражение, сложив тем самым приращения потенциала dV всех подобных рассмотренному тонких слоев, вынеся постоянные – силу тока в источнике, удельное сопротивление среды и 2π – за знак интеграла
HM= Исходя из этого, напряженность поля в М
А плотность тока
Получив основные характеристики нормального поля точечного электрода обратимся к рассмотрению реальной ситуации, когда поле создано с помощью пары электродов АВ (рис.22б), а регистрация осуществляется парой МN. Тогда разность потенциалов
Обозначив расстояние АМ через r1 и AN через r2 можем, учитывая симметрию четырехэлектродной расстановки AMNB относительно центра 0, записать
Учитывая, что r2 – r1 равно расстоянию MN
откуда k – это коэффициент, характеризующий геометрию расстановки. Вполне понятно, что если среда однородная, то есть ρ = const, мы будем получать одно и то же значение ρ при любых k, то есть при любых расстояниях АМ и AN. Однако, в неоднородной среде ρ будет существенно зависеть от k. Эта зависимость обусловлено тем, что плотность тока определяется величиной «разноса» питающих электродов АВ и с увеличением АВ эта относительная плотность с глубиной возрастает, поскольку возрастает и глубина проникновения поля в Землю. Сказанное хорошо видно из рассмотрения такого примера (рис.23). Пусть мы имеем толщу слоев с разным сопротивлением.
Рис.23.Зависимость глубины проникновения электрического поля в слоистую среду от величины разноса питающих электродов АВ.
При малом разносе АВ токовые линии практически целиком размещаются в слое с сопротивлением ρ1. При большем разносе А1В1 поле сосредоточено больше й частью в слое ρ2, здесь плотность тока, отображаемая густотой силовых линий будет наибольшей. С увеличением АВ до А1В1 вычисляемое по приведенной формуле ρ будет уже ближе всего к ρ3 и т.п. В теории электроразведки показано, что отношение тока на глубине h к плотности на поверхности зависит от расстояния между электродами L и при увеличении L эта относительная плотность с глубиной h возрастает по закону
Все сказанное позволяет уяснить идею зондирования среды постоянным током, состоящую в том, что осуществляя серию измерений ΔVMN с разными все возрастающими АВ, мы получаем последовательность значений ρ, характеризующих электрическое сопротивление все более глубоких интервалов геоэлектрического разреза. Такое зондирование называют вертикальным электрическим зондированием ВЭЗ. Помимо ВЭЗ используют другие модификации рассматриваемого метода сопротивлений – ДЭЗ (дипольное электрическое зондирование), ЭП (электропрофилирование) и другие. Во всех этих модификациях основная задача – определение электрической характеристики среды – удельного электрического сопротивления ρ. Однако, что это за ρ? Это в общем случае не ρ1, не ρ2 и не ρ3, а некое ρк – кажущееся сопротивление, зависящее от k (то есть от геометрии 4хэлектродной установки ABMN - от расстояний АВ и MN.), помимо зависимости от этих реальных ρ1, ρ2 и от толщин слоев геоэлектрического разреза. Таким образом, ρк можно определить как удельное электрическое сопротивление такой воображаемой однородной среды, в которой при тех же АВ и MN и при той же силе питающего тока в цепи АВ регистрируется та же разность потенциалов ΔVMN, что и в среде неоднородной. То есть ρк это сложная функция, зависящая от характеристик реального геоэлектрического разреза и от геометрии расстановки
Самое замечательное состоит в том, что в ряде случаев ρк может оказаться как угодно близким к истинным значениям ρ1, ρ2 и т.д. Но это будет показано несколько позже. А пока остановимся на рассмотрении упомянутых модификаций и сделаем это несколько подробнее, чем по ранее представленным методам электроразведки. Но прежде одно замечание, которое должно прояснить читателю, почему и теория методов сопротивлений на постоянном токе и практика их применения разъясняются гораздо обстоятельней, чем это делалось ранее в разделах, посвященных МТЗ и пр.. Дело в том, что эти методы занимают особое место среди других методов электроразведки и геофизики в целом. Во-первых, с методики ВЭЗ и каротажа КС (кажущихся сопротивлений) началась в первой трети двадцатого столетия разведочная геофизика как таковая. Во-вторых, эти методики используются в современной геофизике чаще, чем какой-либо другой метод практически во всех разновидностях полевой геофизики (инженерная, рудная, гидрогеологическая, техническая, археологическая и пр.), за исключением нефтегазовой, хотя история нефтегазовой геофизики тоже ведет свой отсчет именно с этих методик.
Наиболее популярны две разновидности метода сопротивлений: ВЭЗ и электропрофилирование. Для электроразведочных методов вообще характерно такое подразделение - зондирование и профилирование. Зондирования предназначены, главным образом, для исследования горизонтально-слоистых сред, представляющих, в основном, осадочные толщи, а профилирование – для выявления вертикальных или крутонаклоненных неоднородностей, свойственных разрезам с блоковой тектоникой. Сочетание зондирований с профилированием позволяет получить всестороннее объемное представление о строении объектов самой разной природы.
Электропрофилирование. Сущность электропрофилирования заключается в следующем. С учетом эмпирического соотношения глубины h проникновения тока в среду(она зависит от проводимости пород разреза) с величиной питающего разноса АВ: h = Выбранный разнос АВ сохраняется неизменным и эта расстановка АMNВ перемещается вдоль профиля наблюдений. Измерения производятся через определенный интервал, который мотивируется масштабом съемки и геологической задачей.). Обработка результатов наблюдений состоит в вычислении ρк в каждой точке наблюдений и в построении графика зависимости ρк(х). Примеры геологической результативности электропрофилирования покажем на моделях 1 и 2 (рис.24).
Рис.24. Кривые электрического профилирования ρк (х).
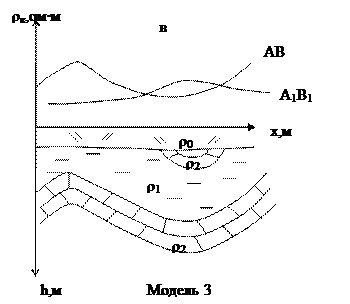
Модель 1. представляет ситуацию, в которой требуется определить плановое положение скрытого под наносами вертикального контакта пород низкого сопротивления ρ1 (осадочная толща) и высокого сопротивления ρ2 (массив кристаллических пород, прорывающих осадочные). Пусть ρ1 ≈ 20 Ом·м; ρ2 = 80 Ом·м; О1, О2 и т.д. - точки, в которых располагаются последовательно центры четырехэлектродной установки AMNВ, с чьей помощью проводятся наблюдения(рис.24а) Пусть толщина наносов, скрывающая положение контакта, составляет 30м. Тогда, выбрав АВ = 80м и размещая последовательно центры электроразведочной установки в точках О1, О2 и т.д. с шагом 50-100 м, мы получим кривую ρк , примерный вид которой показан на рис….Вполне понятно, что пока установка находится далеко слева от зоны контакта, значения ρк. будут близки к ρ1 , напротив, если установка размещена в области больших пикетов О (О7 и далее) ρк станет как угодно близкой к ρ2. В самой приконтактной зоне залегания ρк будет резко изменяться, пока не приблизится к ρ2 . Модель 2 иллюстрирует ситуацию с вертикальными дайками пород высокого сопротивления (рис.24б). Характер полученной кривой можно объяснить, рассуждая таким же образом, как в примере с моделью 1. Нередко возникают такие геологические ситуации, которые требуют контроля за электрической неоднородностью двух или нескольких уровней разреза. Тогда используют так называемые комбинированные установки, например АА'МNB'B. С такой установкой для каждой точки наблюдений О используют два различных разноса питающих электродов АВ и А1В1. При этом вычисляются значения ρк, характеризующие два разных интервала глубин. Примером может послужить ситуация, изображенная на модели 3 (рис.24в). Здесь показан разрез с высокоамплитудными антиклинальной и синклинальной складками, сложенными известняками относительно высокого сопротивления (~150 Ом·м) и терригенной толщей небольшого сопротивления (<50 Ом·м). Видно, что использование больших разносов приведет к пропуску приповерхностной синклинальной формы при правильном воспроизведении особенностей конфигурации глубинного известнякового пласта. В то же время, установка с малым разносом А'В' позволяет выявить пропущенный объект, но не дает адекватного представления о структуре погруженного известнякового пласта. Если вертикальные неоднородности высокого сопротивления выявляются методикой электропрофилирования достаточно контрастно, то наоборот, проводящие тела небольшого размера отмечаются на кривых ρк довольно слабыми пологими минимумами. Поэтому для их выявления используют так называемое комбинированное профилирование. Рассмотрим пример его применения на модели 4, где изображено проводящее вертикальное тело, перекрытое толщей наносов (рис.25). Схема AMNB реализуется через удаленный электрод С и идет поочередно по схеме AMNC и BMNC так, что на каждой расстановке получают два значения ρк : ρкА , когда ток пропускают через А и С и ρкВ (через В и С) – рис.25а
Рис.25.Комбинированное профилирование.
Вдали от проводящего тела над однородной средой ρк будут одинаковыми и для установки AMN∞ (ρкА ) и для BMN∞(ρкВ). Однако, когда установка приближается к проводящему телу, равенство нарушается. Когда установка находится слева, ток стремится к С через тело и плотность тока I возрастает в области MN при пропускании его через А1 и уменьшается при пропускании его через В1. Когда установка находится справа – ситуация обратная (рис.25б). Чем больше плотность тока, тем больше ΔV и, следовательно, ρк . Таким образом, слева от тела появится максимум на кривой ρкА, а справа - на кривой ρкВ. Наличие проводящего тела будет отмечено точкой пересечения кривых ρк с выраженными особыми точками - максимумами и минимумами, тогда как при обычном симметричном профилировании отмечается только слабый минимум (рис. 25в). На участках сложного геоэлектрического разреза с неоднородными условиями заземления электродов используют еще одну модификацию электропрофилирования – метод срединных градиентов с малыми базами MN. Приемная установка MN при этом перемещается вдоль АВ в центральной части, равной 1/3 АВ. Об этой методике и других вариациях профилирования можно прочитать в учебниках по электроразведке, приведенных в списке литературы. Сходны с электропрофилированием по методу сопротивлений на постоянном токе методики магнитотеллурического профилирования и профилирования с использованием искусственно возбуждаемых переменных электрических полей. Там также строятся зависимости ρк (Х) при выбранном неизменном значении параметра, контролирующего глубину проникновения поля в Землю – периода вариации, частоты, времени становления и т.п. Однако, все эти профилирования не дублируют друг друга – каждое имеет свое предназначение, решает разные задачи, исследует разные интервалы глубин. Методика ВЭЗ. Это наиболее важная и востребованная модификации метода сопротивлений, ориентированная, как уже говорилось, на изучение горизонтально-слоистых сред. Сущность ВЭЗ заключается в том, что центр установки О остается на месте, тогда как разнос АВ меняется, то есть меняется глубина зондирования разреза постоянным током и освещается не один-два интервала глубин, а весь разрез. Максимальное расстояние АВ называется величиной зондирования. Начинается оно с малых разносов. Далее разнос увеличивают, но не равномерно, а с все более возрастающими интервалами, например в такой последовательности (в метрах): 2; 5; 10;20; 50;100; 500 и т.д. Условия успешного применения метода: угол наклона границ раздела не должен превышать 10-15º; залегание слоев – согласное; в разрезе имеется толща слоев, сильно отличающихся по сопротивлению от перекрывающих пород, называемая опорным горизонтом. Опорный горизонт должен характеризоваться повсеместным распространением, отображать основные структурные особенности разреза и иметь достаточную мощность для того, чтобы его можно было уверенно выявить по кривой ρк (кривой ВЭЗ). Если зондирование проводится на большую глубину, то местность должна быть подходящей для больших разносов. По вычисленным для каждого разноса АВ значениям ρк строят кривую ВЭЗ на специальных билогарифмических бланках с масштабным модулем М=6,25 см. Вообще электроразведочные построения обычно осуществляют в логарифмическом масштабе, поскольку диапазон изменения ρк для горных пород (от нуля до бесконечности) в линейном масштабе отобразить практически невозможно. Для вычисления ρк используется уже приводившаяся формула ρк = k Измерение силы тока и разности потенциалов могут проводиться с помощью простых приборов, с которыми студент сможет ознакомиться при прохождении учебной геофизической практики. Кривые ВЭЗ Рассмотрим, как выглядят кривые ВЭЗ для различных моделей слоистых сред. Кривые изображают в горизонтальной или вертикальной композиции. Воспользуемся последним способом. Так легче провести аналогию с геологическим разрезом. Двухслойная модель. Представим себе, что скважина вскрыла такой разрез: терригенная толща 1 имеет мощность h1 и сопротивление ρ1 . остальную часть нижнего полупространства занимает карбонатная толща 2 с сопротивлением ρ2 , причем ρ2» ρ1 . ρ и h здесь являются параметрами геоэлектрического разреза, который для рассматриваемых моделей будем представлять в виде пачки плоскопараллельных слоев-пластин, каждая из которых характеризуется своими ρi и hi при горизонтальном залегании. Кривая строится в системе координат ρк = При небольших разносах АВ и, следовательно, концентрации поля в верхних горизонтах разреза значения ρк будут практически неотличимы от ρ1 . Напротив, при очень больших АВ величина ρк вплотную приблизится к ρ2 . Когда разносы окажутся такими, что наибольшей плотностью тока будут характеризоваться приграничные интервалы разреза, значения ρк будут наиболее значимо меняться, возрастая от ρ1 к ρ2 и кривая примет вид, показанный на рис.26, причем точка перегиба кривой будет проектироваться как раз на границы между двумя контактирующими толщами.
Рис.26.Двухслойные кривые ВЭЗ.
Рассмотрим, как будет меняться кривая ВЭЗ при изменениях параметров геоэлектрического разреза ρ и h. Если увеличивать ρ2 , оставляя неизменными ρ1 и h1, можно наблюдать изменение формы кривой при сохранении местоположения точки перегиба. Изменение формы будет определяться тем, что выход ρк на асимптоту ρ2 будет постоянно сдвигаться в сторону больших значений, то есть вправо. Так будет продолжаться до тех пор, пока значения ρк не приблизятся к практической бесконечности, то есть не превысят n·1000ом·м. По достижении таких величин кривая ВЭЗ вырождается в прямую, идущую под углом 45º. Такое вырождение является знаковым показателем ограничения глубинности исследований разреза: постоянный ток не проходит в высокоомный горизонт и точка перегиба кривой диагностирует таким образом гипсометрию опорного горизонта. При обратном соотношении ρ1 и ρ2 (ρ1>ρ2) будет наблюдаться и обратный рисунок кривых ВЭЗ, но выхода кривой на прямолинейную асимптоту здесь уже не будет, так как не может быть бесконечно уменьшена величина ρ2, которая никак не может оказаться меньше нуля (рис.26 б). Поскольку в рассматриваемом случае радикального изменения формы кривой (то есть вырождения ее в прямую) не наблюдается, можно говорить о том, что высокоомные опорные горизонты на кривых ВЭЗ выделяются контрастнее низкоомных. Если изменить местоположение границы h, оставляя неизменным соотношение сопротивлений ρ1 и ρ2,будет наблюдаться иная картина: форма кривой ВЭЗ меняться не будет, но местоположение точки перегиба кривой ВЭЗ, будет перемещаться вслед за перемещением h границы раздела пластов – кривая как бы сдвигается параллельно самой себе(рис.26в). Таким образом, можно констатировать, что кривая ВЭЗ «откликается» на любое изменение параметров геоэлектрического разреза ρ и h либо изменением своей формы, либо перемещением точки перегиба кривой. Существуют специальные палетки таких теоретических кривых, рассчитанных для различных соотношений h и ρ, которые используются в последующей интерпретации результатов ВЭЗ (рис27).
Рис.27.Палетка двухслойных кривых ВЭЗ.
Посмотрим далее, как выглядят трехслойные кривые ВЭЗ(рис.28). Для трехслойной модели можно предусмотреть четыре различных сочетания значений ρ.
Каждое из этих сочетаний определяет тип получаемой кривой ВЭЗ. Этот тип помечается буквенным индексом, показанным в скобках. Начнем с кривых H и A, где последняя толща характеризуется высоким сопротивлением. Трехслойную кривую будем как бы составлять из двух двухслойных, соединяя их общей огибающей. В итоге получается кривая, на которой промежуточная толща отмечается минимумом. По аналогии с уже рассмотренными вариациями параметров геоэлектрического разреза получим выходы кривой на прямолинейную асимптоту при стремлении ρ3→∞. Для трехслойной модели так же можно показать другие преобразования формы кривой при изменении ρ1 и ρ2. Не трудно, например, увидеть, что промежуточный пласт будет тем лучше выделяться на кривой, чем больше его мощность и может вообще «выпасть» (исчезнет минимум, если толщина его окажется слишком малой). Учитывая, что кривая строится в логарифмическом масштабе, можно понять, ч то чем «глубже» кривая, тем эта толщина должна быть больше для того, чтобы минимум появился: для верхних (до 10м) горизонтов разреза это единицы метров, в интервале от 10 до 100 – десятки, за сто – сотни метров и т.д. На кривой типа А промежуточного минимума быть не может, так как сопротивление горизонтов с глубиной нарастает монотонно. Здесь второй пласт будет выделяться зонами градиентных переходов(Рис.28)
.
Рис.28.Трехслойные кривые ВЭЗ. Эти переходы тем контрастнее, чем больше разница сопротивлений контактирующих сред и чем значительнее толщина промежуточного слоя. Высокоомный опорный горизонт так же, как и в предыдущем случае, будет отмечен вырождением кривой в прямую с ростом ρ3. Кривые K и Q обнаруживают обратный рассмотренным характер (рис.28б) и в отношении контрастности их выделения можно сделать те же самые выводы. Ясно, что значение ρк промежуточного пласта будет тем ближе к истинному значению ρк, чем больше его толщина. На рассмотренных примерах вновь можно убедиться в том, что любое изменение параметров геоэлектрического разреза контролируется формой кривой ВЭЗ и местоположением точек перегиба. Для трехслойных моделей также рассчитаны теоретические кривые применительно к разным сочетаниям h и ρ, обозначенные в альбоме палеток. Для моделей с большей слойностью нетрудно построить свои кривые, используя разные композиции двух и трехслойных кривых. Интерпретация кривых затруднена сильным проявлением эквивалентности. Она заключается в том, что по кривым для промежуточного пласта могут быть определены не ρ и h в отдельности, а только так называемая продольная проводимость ρi = hi/ρ для кривых Н и А (поскольку для таких моделей ток «отжимается» непроводящей толщей ρ3 и течет вдоль ее поверхности) или поперечное сопротивление Ti = hiρi для моделей K и Q (поскольку в этом случае ток течет поперек напластования, стремясь попасть в проводящую толщу ρ3). Отсюда следует, что при определенном сочетании hi и ρi, когда S или Т не меняется, форма кривой так же остается неизменной. Прежде чем перейти к рассмотрению вопросов интерпретации кривых ВЭЗ, приведем пример многослойной кривой ВЭЗ (рис.29).
Рис.29.Пятислойная кривая ВЭЗ.
То, что по этой кривой можно выделить в разрезе 5 геоэлектрических слоев различного состава и толщины, не означает, к сожалению, что этот разрез и на самом деле таков. Если нашу установку AMNB поставить вертикально и опустить в скважину с тем, чтобы провести в реальном масштабе глубин регистрацию ρk с определенным интервалом наблюдения, то на такой скважинной (каротажной) кривой можно будет выделить в зависимости от выбранного разноса десятки различных слоев. То есть разрешающая способность полевого ВЭЗ, определяемая и сложным характером зависимости ρk от соотношения сопротивлений и мощностей множества пластов, и использованием логарифмического масштаба изображений, несопоставима с возможностями скважинных исследований. Тем не менее, наиболее существенные крупные комплексы проводящих и непроводящих пород глубинного разреза и достаточно тонкие слои верхней его части выделяются на кривых ВЭЗ достаточно уверенно. Таким образом, становится понятным как определить геологическую природу отмеченных особенностей рельефа кривых. Определить геологическую природу аномалий – максимумов, минимумов, участков ограниченных резкими градиентными изгибами кривой – это значит поставить им в соответствие тот или иной комплекс пород разреза. Это можно сделать с достаточной надежностью, если в распоряжении исследователя есть результаты бурения или в худшем случае сейсморазведки. И, конечно, тогда, когда интерпретатор имеет достаточно четкое представление об электрических свойствах горных пород. Как уже отмечалось выше, важнейшим таким свойством является удельное электрическое сопротивление(или обратная ему величина-проводимость). Сопротивление пород изменяется в очень широких пределах: от 10-5 до 1015 Ом·м, то есть практически от 0 до ∞. Зависит величина сопротивления от минерального состава, физико-механических и водных войств пород, а также от температуры, глубин залегания, степени метаморфизма и пр. Удельное электрическое сопротивление минералов определяется характером их внутренних кристаллических связей. Так, минералам диэлектрикам (кварц, слюды полевые шпаты и др.) с преимущественно ковалентными связями присущи очень высокие сопротивления (1012-1015Ом·м). Минералы полупроводники (карбонаты, сульфиды, галоиды и др.) имеют ионные связи и отличаются высокими сопротивлениями (104 - 108 Ом·м). Глинистые минералы (гидрослюды, монтмориллонит, каолинит и др.) обладают ионно-ковалентными связями и характеризуются относительно низким сопротивлением (ρ<50Ом·м). Рудные минералы (самородные, сульфиды, некоторые оксиды) с электронной проводимостью очень хорошо проводят ток (ρ<5Ом·м). Первые две группы минералов составляют «жесткий» скелет большинства горных пород. Глинистые минералы создают «пластичный» скелет. «Пластичные» минералы способны адсорбировать «связанную воду» с достаточно постоянной минерализацией и хорошей проводимостью и поэтому сопротивление глин довольно низкое и мало меняется (6 – 20 Ом·м). В то же время породы с жестким скелетом могут насыщаться лишь свободной водой, проводимость зависит от степени ее минерализации. Сопротивление такой воды изменяется от сотых долей Ом·м при высокой общей минерализации (М>10 г/л) до сотен Ом-м при низкой минерализации (М<0,01 г/л). Поэтому проводимость осадочных пород целиком определяется их пористостью, трещиноватостью и влагонасыщенностью. Терригенные песчанистые породы всегда характеризуются более или менее значительной пористостью и являются в большинстве случаев хорошими проводниками. Проводимость их существенно ухудшается, если поры насыщенны пресной водой и совсем исчезает, когда флюид имеет углеводородный состав (нефть совсем не проводит электричества). Карбонатные породы в большинстве случаев имеют очень низкую пористость, то есть довольно высокое сопротивление (ρ>102Ом·м). Однако, трещиноватые и кавернозные их разности, не говоря уже об известняках органогенного генезиса или измененных деформацонной переработкой. В таких известняках могут возникать крупные скопления минерализованных и пресных вод, а также нефтегазовые залежи. Глубина залегания, степень метаморфизма, структура и текстура породы также влияют на ее сопротивление, изменяя коэффициент микроанизотропии λ= Чаще всего λ изменяется от 1 до 1,5, достигая 2 – 3 у сильно рассланцованных пород. Несмотря на широкий диапазон изменения сопротивлений ρ у разных пород можно говорить о достаточно устойчивых оценках ρ, встречающихся в практике электроразведки. Кристаллические (магматические и метаморфические) породы характеризуются высокими сопротивлениями от 500 до 10 000 Ом·м. Среди осадочных пород высокие сопротивления свойственны известнякам, гипсам и особенно каменной соли (100 – 1000 Ом·м). Обломочные осадочные породы, глины, суглинки, супеси имеют сопротивление от долей до первых десятков, иногда до ста Ом·м. Среди других электрических свойств пород можно назвать уже упоминавшуюся электрохимическую активность, пьезоэлектрические свойства, диэлектрическую и магнитную проницаемость, поляризуемость. Поляризуемость η является довольно востребованным параметром в рудной и нефтегазовой геофизике. Электроразведочный метод, основанный на различной поляризуемости пород называется методом вызванной поляризации. Его особенно часто применяют в комплексе с ВЭЗ или ЭП. Поляризуемость (или коэффициент поляризуемости) η оценивает способность пород поляризоваться, то есть накапливать заряд при пропускании тока, а затем разряжаться после его отключении. Значения η вычисляют в процентах, как отношение разности потенциалов ΔUВП, которое остается в цепи MN по истечении определенного времени (обычно 0,5 – 1 сек) после размыкания токовой цепи к напряжению ΔU при пропускании тока η = Наибольшей поляризуемостью (η = 6÷40%) отличаются руды с электронной проводимостью. Нередко само рудное тело, вследствие своих небольших размеров, не представляет разведочного интереса и выражается на кривой ρк (х) при электропрофилировании или очень слабо или вообще остается незамеченным. Однако ореол вкрапленных руд, электрически не связанных между собой, может быть очень значительным и представлять собой достаточно крупное месторождение. Такие ореолы вообще не фиксируются методом сопротивлений, но поляризуемость над скоплениями рудных вкраплений существенно (на порядок) превышает фоновые значения и создает интенсивные аномалии η (рис. 30)
Рис.30. Аномалия ВП над месторождением вкрапленных руд.
Возникновение вызванных потенциалов в таких ситуациях объясняют так называемой электронной поляризацией руд в присутствии подземных вод. Коэффициенты поляризуемости до 2 – 6 % наблюдаются над обводненными или нефтеносными рыхлыми осадочными породами с примесью глинистых частиц. В этих породах при пропускании тока происходит перераспределение и диффузия зарядов, адсорбированных на глинистых частицах. Возвращение среды в состояние равновесия после отключения тока сопровождается эффектом вызванной поляризации. Большинство магматических и метаморфических пород, как правило, не поляризуется, у них η = 1÷2%. Слабо поляризуются и породы, насыщенные минерализованной водой. Далее попробуем составить какое-то представление об интерпретации материалов ВЭЗ. Интерпретация кривых ВЭЗ В геофизике и, в частности, в электроразведке издавна сложилось понятие качественной и количественной интерпретации данных. Под качественной интерпретацией как раз и понимается установление геологической природы выявленных аномалий и выявление их плановых конфигураций на картах. А под количественной интерпретацией понимается определение геометрии и свойств источников этих аномалий. Среди многочисленных документов качественной интерпретации электроразведочных данных весьма популярными являются карты типов кривых и карты изоом ρк для фиксирования разносов АВ. Карты типов кривых составляются для того, чтобы выделить площади, в пределах которых наблюдаются кривые одного типа, то есть однотипный геоэлектрический разрез. Тип кривой определяется числом выделяемых на ней слоев. Карта составляется следующим образом: на планшет в соответствующем масштабе выносятся все точки центров зондирования и возле каждой точки выписывается цифровой индекс, указывающий тип кривой. Затем проводятся линии, разграничивающие области существования кривых разного типа. В итоге получается аналог важнейшего геологического документа - геологической карты. На рис.31 иллюстрируется идея построения карты типов кривых на примере рассмотрения профиля таких кривых, где хорошо видно как отображается на такой карте антиклинальная складка, в ядре которой под наносами с сопротивлением ρ0 картируются более древние породы (3-слойные кривые) и по периферии – бол
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 419; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.26.8 (0.016 с.) |


 , где U1 и U2 значения потенциала на концах проводника, а R – его сопротивление R=ρ
, где U1 и U2 значения потенциала на концах проводника, а R – его сопротивление R=ρ  и, соответственно, ΔU = JR= Jρ
и, соответственно, ΔU = JR= Jρ 







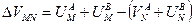

 , обозначив π
, обозначив π  через k,
через k, , а
, а  .
.

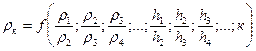
 ÷
÷  АВ -подбирается такая величина разноса, которая гарантирует достижение необходимой глубины исследования.
АВ -подбирается такая величина разноса, которая гарантирует достижение необходимой глубины исследования.
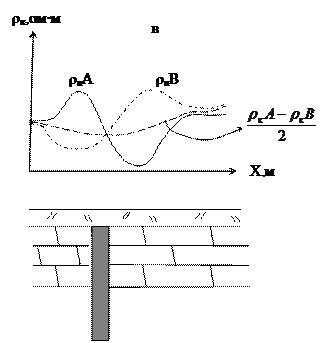


 , так как
, так как  это вероятная глубина проникновения тока в Землю. Горизонтальная пунктирная линия на графике ρк =
это вероятная глубина проникновения тока в Землю. Горизонтальная пунктирная линия на графике ρк = 




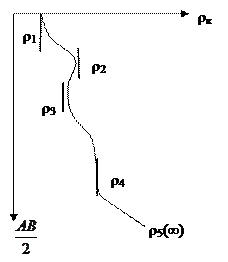
 , где ρn и ρl – сопротивление породы вкрест и вдоль слоистости.
, где ρn и ρl – сопротивление породы вкрест и вдоль слоистости. ·100%
·100%



