
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение второй производной к выпуклости функции и к точкам перегиба. Вертикальная и наклонная асимптоты графика функции.
Опр.1. а) График дифференцируемой функции y=f(x) называется выпуклым вниз на интервале (a;b), если он расположен выше любой ее касательной на этом интервале. б)График функции называетсяy=f(x) выпуклым вверх на интервале (a;b), если он расположен ниже любой ее касательной на этом интервале. Теорема: если функция y=f(x) во всех точках интервала (a;b) имеет отрицательную вторую производную, т.е. f″ (x)˂ 0, то график функции в этом интервале выпуклый вверх. Если же f″ (x)˃ 0, то график функции в этом интервале выпуклый вниз. Точка перегиба - точка графика непрерывной функции y=f(x), определяющая его части разной выпуклости. Достаточное условие существования точек перегиба: Если вторая производная f″ (x) при переходе через точку x ₒ, в которой она равна нулю или не существует, меняет знак, то точка графика с абсциссой x ₒ есть точка перегиба Вертикальная, горизонтальна и наклонная асимптоты Асимптотой кривой называется прямая, расстояние до которой от точки кривой y=f(x) стремится к 0 при х→х0, (.)х может быть ∞, а х0= Вертикальная асимптота: Прямая x=a является вертикальной асимптотой графика функции y=f(x), если:
Наклонная асимптота: Уравнение наклонной асимптоты: y=kx+b. Если существует наклонная асимптота y=kx+b, то k и b находятся по формулам:
Верно и обратное утверждение: если существуют конечные пределы (1) и (2), то прямая y=kx+b является наклонной асимптотой. Если хотя бы один из пределов (1) или (2) не существует или равен бесконечности, то кривая y=f(x) наклонной асимптоты не имеет В частности, если k =0, то y =b. Поэтому y=b – уравнение горизонтальной асимптоты. Асимптоты графика функции y=f(x) при x →+∞ и x →−∞могут быть разными. Поэтому при нахождении пределов (1) и (2) следует отдельно рассматривать случай, когда x →−∞ и когда x →+∞ Первообразная. Неопределенный интеграл, его основные свойства. Таблица основных интегралов. Опр.1. Функция F(x) называется первообразной функции f(x) на интервале (a;b), если для любого x Опр.2. Совокупность всех первообразных φ(x) x Таким образом, по определению
Здесь f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением, x – переменной интегрирования, ∫- знаком неопределенного интеграла. Теорема о существовании неопределенного интеграла: если функция y=f(x) непрерывна на (a;b), то для f(x) существует первообразная, а тогда существует и неопределенный интеграл. Пусть F(x) – первообразная функции f(x), где Док-во: рассм. правую часть (2) (F(x)+C)′= F′(x)+C′=f(x)⇒ F(x)+C – первообразная функции f(x) Пусть φ(x) – другая первообразная функции f(x), причем T(x)≠F(x), тогда t′(x)=f(x) для Сво-ва неопредел. Интеграла. 1) Дифференциал от интеграла d(S(f(x)dx)=d(F(x)+C=dF(x)+dC Док-во: (S(f(x)dx)=d(F(x)+C=dF(x)+dC=dF(x)=F′(x)dx Следствия (f(x)dx)′=f(x)dx 2) 3) 4) Инвариантность форм интегрирования Пусть F(x) – первообразная f(x)
Таблица интегралов:
21. Непосредственное интегрирование, подведение заданного выражения под знак дифференциала, примеры. Замена переменной в интеграле, подстановка. Интегрирование по частям, типы интегралов, для которых применяется интегрирование по частям. П.1 метод интегрирования, при котором данный интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств неопределенного интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием. При сведение данного интеграла к табличному часто используются следующие преобразования дифференциала («подведение под знак дифференциала»):
Замена переменной в интеграле Метод интегрирования подстановкой заключается в введении переменной интегрирования. При этом интеграл приводится к новому интегралу, который является табличным или к нему сводится. Пусть требуется вычислить интеграл
Метод интегрирования по частям Пусть u=u(x) и V=V(x) – функции, имеющие непрерывные производные. Тогда d(uv)=u∙dv + v∙du. Интегрируя это равенство, Полученная формула называется формулой интегрирования по частям. Она позволяет свести вычисление интеграла Типы интегралов, для которых удобен метод интегрирования по частям. 1) Интегралы вида 2) Интегралы вида 3) Интегралы вида 22. Дробно – рациональная функция (рациональная дробь). Четыре типа простейших дробей. Теорема о разложении рациональной дроби. Метод неопределенных коэффициентов, пример. Опр.1. Дробно – рациональной функцией или рациональной дробью называется отношение многочленов: Утв. Неправильную рациональную дробь можно представить в виде суммы многочлена и правильной рациональной дроби. Например: 4 типа простейших рациональных дробей 1) 2) 3) 4) Теорема 1. Разложение правильно1 рациональной дроби на сумму простейших дробей: Пусть прав. рацион. дробь
Для нахождения неопределенных коэффициентов используется метод уравнения левой и правой части. Идея метода сравнения: 1) В правой части равенства (2) приводим к общему знаменателю 2) Т.е. в полученном равенстве равны знаменатели, а числители равны: Pn(x)=S(x) 3) Сравниваем коэф. при одинаковых степенях x, получим систему алгебраических линейных уравнений, относительно коэф. A,A1…B,B1. Замечания: при нахождении неорп. коэф. в третьем пункте используют иногда смешанный прием, т.е. пусть x=x1; x=x2, из которых определяют неопр. коэф., если остаются неопр.коэф. применяют метод сравнения.
|
||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 241; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.251.155 (0.012 с.) |

 (существует, если есть точки разрыва)
(существует, если есть точки разрыва) (1)
(1) (2)
(2) (a;b) выполняется равенство F′(x)=f(x) (1)
(a;b) выполняется равенство F′(x)=f(x) (1)
 ; тогда
; тогда  (2)
(2)
 - линейность
- линейность ; U=T(x) -
; U=T(x) -  функция,
функция,  , где F(u) – первообразная функции f(u)
, где F(u) – первообразная функции f(u) 2)
2)  3)
3) 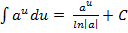 4)
4)  5)
5) 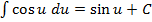 6)
6)  7)
7)  8)
8)  9)
9) 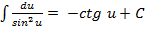
 11)
11)  12)
12)  13)
13)  14)
14) 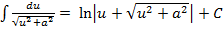 15)
15) 

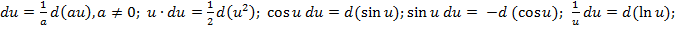

 . Сделаем подстановку x=φ(t), где φ(t) – функция, имеющая непрерывную производную. Тогда dx=φ′(t)dt на основании св-ва инвариантности формулы интегрирования неопр. интеграла получаем формулу интегрирования подстановкой:
. Сделаем подстановку x=φ(t), где φ(t) – функция, имеющая непрерывную производную. Тогда dx=φ′(t)dt на основании св-ва инвариантности формулы интегрирования неопр. интеграла получаем формулу интегрирования подстановкой: 

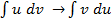 , который является более простым или табличным.
, который является более простым или табличным. ,
, 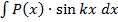 ,
,  – многочлен, k – число. Удобно u=P(x), dv – все остальное
– многочлен, k – число. Удобно u=P(x), dv – все остальное ,
, 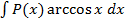 ,
, 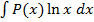 ,
,  ,
,  . Удобно: P(x)dx=du, а за u обозначить остальные сомножители.
. Удобно: P(x)dx=du, а за u обозначить остальные сомножители. ,
,  , где a и b – числа. За u можно принять функцию u=eax.
, где a и b – числа. За u можно принять функцию u=eax.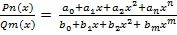 (1), если n
(1), если n  m, то дробно – рациональная функция неправильная, если n<m, nj (1) – правильная
m, то дробно – рациональная функция неправильная, если n<m, nj (1) – правильная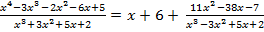
 ; A,a – const
; A,a – const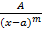 ; m≥2, m
; m≥2, m 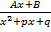 ; A,B,p,q – const, D=p2-4q<0
; A,B,p,q – const, D=p2-4q<0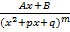 ; m≥2; D<0
; m≥2; D<0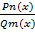 , n<m, Qn(x)=(x-x1)(x-x1)2…(x-x1)k1(x-x2)…(x-x2)k2…(x2+px+q)…(x2+p0x+qu)qu , где действ. корни: х1, х2… имеют кратность соответственно k1,k2. тогда рацион. дробь представляется в виде суммы простейших дробей.
, n<m, Qn(x)=(x-x1)(x-x1)2…(x-x1)k1(x-x2)…(x-x2)k2…(x2+px+q)…(x2+p0x+qu)qu , где действ. корни: х1, х2… имеют кратность соответственно k1,k2. тогда рацион. дробь представляется в виде суммы простейших дробей. (2)
(2) - неопределенные коэффициенты
- неопределенные коэффициенты , где S(x) – многочлен в неопр. коэф.
, где S(x) – многочлен в неопр. коэф.


