
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация точек разрыва функций и графики для них.
Пусть y=f(x) не выполняется равенство 1) f(x) определена в U(x0), но 2) 3) Точки разрыва: 1) Точки разрыва I рода: · Устранимая точка разрыва A1=A2 · Точка конечного разрыва если А1≠А2, при этом |А1-А2| называется скачком функции в точке разрыва ((.)х0) 2) Точки разрыва II рода:
Задачи, приводящие к понятию производной. Определение производной, ее механический и геометрический смысл. Уравнения касательной и нормали к кривой. Задачи, приводящие к понятию производной Зависимость между непрерывностью и дифференцируемостью функций. Гладкая функция. Правила дифференцирования. Теорема 1. Пусть y=f(x) дифференцируема в (.)х0⇒она непрерывна в ней. Обратное утверждение неверно. Если функция y=f(x) непрерывна в(.) или на интервале, то она не обязательно дифференцируема в (.) или на интервале. Следствия: если функция не дифференцируема в (.) х0, то в (.)х0 Теорема 2. Для того, чтобы функция y=f(x) была дифференцируема в (.) Опр. 1. Если функция y=f(x) имеет непрерывную производную y′=f′(x), где Правила дифференцирования. Пусть U=U(x), V=V(x) дифференцируема на (a,b) ( 1) Сумма и разность функций дифференцируема на (a,b): (U(x) 2) Произведение функций дифференцируемо на (a,b), причем: (U(x)∙V(x))′=U′(x)∙V(x) + V′(x)∙U(x) 3) Частое функций дифференцируемо на (a,b), если V(x)≠0, где Следствие из 2): 1) (C∙U(x))′=C∙U′(x), где C-любая const 2) Свойство линейности Производная сложной и обратной функций. Таблица производных элементарных функций. Теорема 1. Пусть функция y=f(x) имеет производную в (.)х0, т.е. Замечание: теорема дифференцирования сложной функции распространяется на конечное число вложений функции. Z(t)=z(φ(y(t))), при этом существует z′φ, φ′y, y′t, то z′(t)= z′φ∙φ′y∙ y′t
Теорема 2. Пусть y=f(x) строго монотонна на (a,b). Иначе: Производная обратной функции равна обратной величине производной данной функции. Таблица производных:
14. Дифференцирование неявных и параметрически заданных функций. Логарифмическое дифференцирование, пример. Пусть y=f(x) на [a,b], то говорят, что функция задана явно. Однако функция может быть задана неявно и параметрически. Опр.1. Функция задана неявно на интервале (a,b), если она определяется уравнением f(x,y)=0 (1), не разрешенным относительно y. Замечания: Правило1. Нахождение y′(x) для функции, заданной неявно уравнение (1): 1) Дифференцируем уравнение(1) по переменной х, рассматривая при этом y как функцию y(x). 2) Из полученного уравнения выражаем y′(x) Опр.2. y=f(x) задана параметрически, если независимая переменная х и зависимая переменная y связаны между собой параметрической системой уравнений: x=x(t); y=y(t); 1) Пусть 2) X(t) имеет обратную функцию t(x) Правило 2. Дифференцирование параметрически заданной функции с помощью (2) 1) Вычислить производные x′(t), y′(t) 2) По правилу дифференцирования сложной функции y=y(t)=y(t(x)) имеем y′(x)=y′(t)∙t′(x) 3) По правилу дифференцирования обратной функции из полученного равенства имеем: Иногда при нахождении производных от сложных функций применяют логарифмическое дифференцирование. Правило 3. 1) Исходную функцию логарифмируют 2) Полученную логарифмическую функцию дифференцируют и выражают y′(x) Правило 3 применяют для степенно-показательных функций. Утверждение: y=U(x)V(x) Справедлива формула дифференцирования:
|
|||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.112.1 (0.012 с.) |
 или
или  , то есть функция y=f(x) не является непрерывной в (.)х0. Такая точка называется точкой разрыва. Она является точкой разрыва, если выполняется, хотя бы одно и условий:
, то есть функция y=f(x) не является непрерывной в (.)х0. Такая точка называется точкой разрыва. Она является точкой разрыва, если выполняется, хотя бы одно и условий: f(x0)
f(x0)


 ;
; 
 чтобы
чтобы  (a,b), то эта функция называется гладкой.
(a,b), то эта функция называется гладкой.
 V(x))′=U′(x)
V(x))′=U′(x)  V′(x)
V′(x)
 , где α, β – const
, где α, β – const обратная функция x=φ(y) имеет производную φ′(y), при этом справедлива формула φ′(y)=
обратная функция x=φ(y) имеет производную φ′(y), при этом справедлива формула φ′(y)= 
 ; следствие:
; следствие:  5)
5) 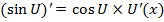 6)
6)  7)
7)  8)
8) 
 10)
10)  11)
11)  12)
12)  13)
13) 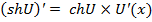 ;
;  14)
14) 
 15)
15)  ;
;  16)
16)  ;
; 
 функцию, заданную явно: y=f(x) можно записать неявно: y=-f(x)=0
функцию, заданную явно: y=f(x) можно записать неявно: y=-f(x)=0 (2)
(2) t для всех
t для всех  (3)
(3)



