
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предел функции в точке и на бесконечности. Односторонние пределы. Бесконечно большая функция.
· Опр.1. Число А называется пределом функции y=f(x) в точке х0, если для любой последовательности допустимых значений аргумента хn, · Опр.2(по Коши). · Замечания: в опр. 1 и 2 (.)х→(.)х0 различным способом. Рассматривают однако случаи когда (.) х→(.)х0 слева и справа. · Опр. 3. Число В называется пределом функции y=f(x) слева в (.) х0, если · Опр.4. Число А называется пределом функции y=f(x) слева в (.) х0, если · Опр.5. Число А называется пределом функции y=f(x) при · Опр.6. Функция называется бесконечно большой, при х→х0, если Обозн. Опр.7. Функция y=f(x) называется бесконечно большой при х→∞, если · Замечания: в вышеприведенных определениях Бесконечно малые функции, их свойства. Связь между функцией, пределом и бесконечно малой функцией. Основные теоремы о пределах функций. · Опр.1. Функция y=f(x) называется бесконечно малой при х→х0, если · Замеч. Функция y=f(x) может быть б.м.ф. и при х→х0-0, и при х→х0-0, в этих случаях f(x)→0 Свойства бмф. 1) Алгебраическая сумма конечного бмф есть бмф. 2) Произведение бмф на ограниченную функцию есть бмф. Следствие: a) Произведение бмф есть бмф b) Частное бмф на функцию, предел которой отличен от 0, есть бмф c) Произведение бмф на число есть бмф 3) Пусть Теорема 1. Связь между функцией, ее пределом и бмф. Если функция y=f(x) имеет предел:
Основные теоремы о пределах функций. Теорема 1. Предел суммы (разности) двух функций равен сумме (разности) их пределов:
Теорема 2. Функция может иметь только один предел при Теорема 3. Предел произведения двух функций равен произведению их пределов:
Теорема 4. Постоянный множитель можно выносить за знак предела: Теорема 5. предел степени с натуральным показателем равен той же степени предела: Теорема 6. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не равен нулю:
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 340; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.108.186 (0.009 с.) |
 , сходящейся к х0, последовательность соответствующих значений функции f(xn),
, сходящейся к х0, последовательность соответствующих значений функции f(xn), 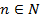 , сходится к числу А. Обозначение:
, сходится к числу А. Обозначение: 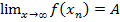

 такое положительное число
такое положительное число  , что
, что  и удовлетворяющий неравенству
и удовлетворяющий неравенству 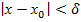 ,будет выполняться неравенство |f(x)-A|
,будет выполняться неравенство |f(x)-A| 
 , что для
, что для 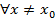 и удовлетворяющего условию х-х0> -
и удовлетворяющего условию х-х0> - 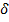 , т.е.
, т.е. 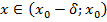 , выполняется условие |f(x)-В|
, выполняется условие |f(x)-В| 
 , что для
, что для 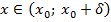 , выполняется условие |f(x)-A|
, выполняется условие |f(x)-A| 
 , если
, если  , что для
, что для  удвл.неравенству |x|>M выполняется неравенство |f(x)-A|
удвл.неравенству |x|>M выполняется неравенство |f(x)-A| 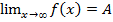
 , что
, что 
 , что |х|>
, что |х|>  . Обозн.
. Обозн. 
 . Пример бесконечно большой функции
. Пример бесконечно большой функции  , т.к.
, т.к. 
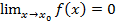 . Данное равенство обозначает:
. Данное равенство обозначает:  , что |х→х0|<
, что |х→х0|< 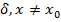 и выполняется неравенство |f(x)|<
и выполняется неравенство |f(x)|< 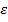 . Обозн. Б.м.ф.:
. Обозн. Б.м.ф.: 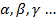
 бмф при х→х0
бмф при х→х0  – ббф, при х→х0. Верно и обратное.
– ббф, при х→х0. Верно и обратное. , то ее можно представить в виде:
, то ее можно представить в виде: , где
, где 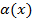 -бмф при х→х0. Верно и обратное.
-бмф при х→х0. Верно и обратное.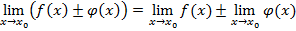
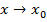


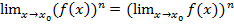 . В частности
. В частности 




