
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производные высших порядков. Механический смысл производной второго порядка. Производные высших порядков функций, заданных неявно и параметрически.
Производные высших порядков Если функция f′(x) дифференцируема, то ее производная называется производной второго порядка и обозначается y′′. Таким образом f′(x)=(f′(x))′ Опр.1. производной n-ого порядка (или n-ой производной) называется производная от производной n-1 порядка: y(n)=f(n-1)(x) Производные n-ого порядка называются производными высшего порядка. Замечания: f(0)(x)=f(x) Механический смысл производной второго порядка Пусть материальная точка P движется по закону S=S(t)
S′(t)=V(t) – скорость (.)P ⇒ S′′(t)=V′(t)=a(t) – ускорение S′′(t)= Производные высших порядков от неявных и параметрически заданных производных I: если функция задана неявно f(x,y)=0 (3), то для нахождения производной 2 порядка y′′(x) необходимо: 1) Продифференцировать (3) по (х) 2) Выразить y(x) из полученного уравнения 3) Продифференцировать выражение из п.2 4) Подставить y′ в выражение п.3 5) Выразить y′′(x) из п.4 II: если функция задана параматрически системой уравнений То по формуле Тогда из (5):
Дифференциал функции и его геометрический смысл. Теоремы о дифференциалах. Применение дифференциала к приближенным вычислениям. Пусть y=f(x) имеет f′(x)≠0 Тогда по теореме о связи предела функции (предела функции, функции и бмф) Бмф: Опр.1. главная линейная часть приращения функции Δy называется дифференциалом функции f(x) и обозн. dx=f′(x)Δx dx = Δx df=f′(x)dx дифференциал функции равен произведению f′(x) на дифференциал независимой переменной. Геометрический смысл дифференциала: Дифференциал функции y=f(x) d (.)x равен приращению ординаты касательной к графику функции в этой точке, тогда (.)х получают приращение Δх. Следствие: (.)L(x+Δx;y+Δy) Основные теоремы о дифференциалах Теорема1. Об арифметических операциях дифференциала. Дифференциал суммы, разности, произведения и частного двух дифференцируемых функций U=U(x), V=V(x) выражаются формулами: 1) 2) 3) Теорема 2. Дифференциал сложной функции Дифференциал сложной функции равен произведению производной этой функции по промежуточному аргументу на дифференциал этого промежуточного аргумента.
Пусть y=f(φ(x)), где U=φ(x), x Следствие: Инвариантность (неизменность) формы первого дифференциала.
Сравнивая (1) и др.§ заметим: 1 дифференциал функции y=f(x) определяюся одной и той же формулой, независимо от того, является ее аргумент зависимой или независимой переменной. Замечания 1. Пусть y=f(U), U=φ(x), тогда U-зависимая переменная, а х – независимая переменная⇒dU≠ΔU а d(x)≠Δx Замечание 2. Таблица дифференциалов аналогична таблице производных.
|
|||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 1127; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.105.41 (0.005 с.) |
 (1)
(1) , где
, где  - среднее ускорение (.)Р за время Δt
- среднее ускорение (.)Р за время Δt (4)
(4) (5)
(5) (6)Аналогично считается 3-его и выше порядков.
(6)Аналогично считается 3-его и выше порядков. (по определению производной)
(по определению производной) ;
; 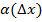 -бмф при Δх→0
-бмф при Δх→0



 (a,b)
(a,b)  (1) U-промежуточный аргумент
(1) U-промежуточный аргумент и
и 



