
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Доверительный интервал для оценки математического ожидания нормального распределения случайной величины с известным sСодержание книги
Поиск на нашем сайте
Пусть случайная величина X имеет нормальное распределение с неизвестным математическим ожиданием Задаем достаточно высокую доверительную вероятность g. Требуется построить доверительный интервал
Вероятность попадания случайной величины
где Обозначая
Задача. Случайная величина X имеет нормальное распределение с известным s=3. Найти доверительный интервал для оценки неизвестного математического ожидания а по его выборочному среднему Решение. Имеем
Из табл. 4 t = 1,96. Тогда
2. Доверительный интервал для оценки математического ожидания В отличие от предыдущего, случайная величина X имеет нормальное распределение N (a,s) с неизвестным s. Пусть произведено n независимых испытаний, построены выборочная средняя Рассмотрим случайную величину
Распределение является t – распределение или распределением Стьюдента с Действительно, по определению, если Случайная величина
распределена также по нормальному закону (как линейная функция относительно нормального аргумента Известно, что случайная величина
распределена по закону c2 с С ростом степеней свободы распределение Стьюдента приближается к нормальному
Обозначая Таким образом, имеем
Значение
Задача 5.3.2. Случайная величина X имеет нормальное распределение. По выборке объемом n = 15 найдены выборочная средняя Решение. По табл. 5 приложения находим
Замечание. Пусть производится n независимых равноточных измерений некоторой физической величины, истинное значение которой Задача 5.3.3. По данным 16-ти независимых равноточных измерений физической величины найдено выборочное среднее Решение. Истинное значение измеряемой величины равно ее математическому ожиданию Используя табл. 5 приложения по
|
||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 374; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

 и известной дисперсией s2. Пусть произведено n независимых опытов и на основании статистических данных получено выборочное среднее:
и известной дисперсией s2. Пусть произведено n независимых опытов и на основании статистических данных получено выборочное среднее: 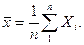
 . Прежде всего, заметим, что случайная величина
. Прежде всего, заметим, что случайная величина  также имеет нормальное распределение
также имеет нормальное распределение  . Действительно,
. Действительно, ;
; 

 – функция Лапласа.
– функция Лапласа.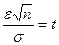 , имеем Ф (t) = g/2. Затем по табл. 4 приложения находим t по значению Ф (t) = g/2; отсюда находится
, имеем Ф (t) = g/2. Затем по табл. 4 приложения находим t по значению Ф (t) = g/2; отсюда находится  :
:  . Таким образом, доверительный интервал имеет вид
. Таким образом, доверительный интервал имеет вид
 .
. , если известны объем выборки
, если известны объем выборки  и
и 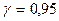 .
.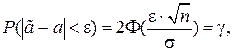 t =
t =  ,
,  .
. . Таким образом,
. Таким образом, .
. .
. степенями свободы.
степенями свободы. – случайная величина с нормальным распределением
– случайная величина с нормальным распределением  , а V – случайная величина, распределенная по закону c2 с k степенями свободы, то случайная величина
, а V – случайная величина, распределенная по закону c2 с k степенями свободы, то случайная величина  распределена по закону Стьюдента с k степенями свободы.
распределена по закону Стьюдента с k степенями свободы. . Случайная величина
. Случайная величина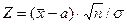

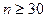 практически не отличается от него. Следовательно, при оценке неизвестных параметров по выборке малого объема
практически не отличается от него. Следовательно, при оценке неизвестных параметров по выборке малого объема 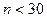 используют распределение Стьюдента При построении доверительного интервала для математического ожидания речь идет о вероятности Имеем
используют распределение Стьюдента При построении доверительного интервала для математического ожидания речь идет о вероятности Имеем или с учетом
или с учетом .
. , получаем
, получаем  .
.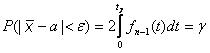 .
. определяется по вероятности
определяется по вероятности  из табл. 5 приложения распределения Стьюдента. Затем, принимая во внимание, что
из табл. 5 приложения распределения Стьюдента. Затем, принимая во внимание, что  , находим
, находим  . Таким образом, доверительный интервал для оценки математического ожидания с неизвестным s имеет вид
. Таким образом, доверительный интервал для оценки математического ожидания с неизвестным s имеет вид .
. , “исправленное” среднее квадратическое отклонение
, “исправленное” среднее квадратическое отклонение  . Определить интервальную оценку математического ожидания с доверительной вероятностью
. Определить интервальную оценку математического ожидания с доверительной вероятностью  .
. . Тогда
. Тогда 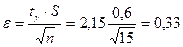 . По формуле (5.3.11) получим доверительный интервал
. По формуле (5.3.11) получим доверительный интервал .
. – результаты отдельных измерений, рассматриваемые как независимые случайные величины с одним и тем распределением, и имеют одно и то же математическое ожидание (истинное значение измеряемой величины), одинаковые дисперсии s2 (измерения равноточные). В этом случае истинное значение измерений физической величины оценивается с помощью среднего выборочного
– результаты отдельных измерений, рассматриваемые как независимые случайные величины с одним и тем распределением, и имеют одно и то же математическое ожидание (истинное значение измеряемой величины), одинаковые дисперсии s2 (измерения равноточные). В этом случае истинное значение измерений физической величины оценивается с помощью среднего выборочного  , для которого можно построить доверительный интервал (с неизвестным s) по методу, указанному в п. 2.
, для которого можно построить доверительный интервал (с неизвестным s) по методу, указанному в п. 2. и “исправленное” среднее квадратическое отклонение
и “исправленное” среднее квадратическое отклонение  . Требуется оценить истинное значение случайной величины с надежностью
. Требуется оценить истинное значение случайной величины с надежностью  , находим
, находим  . Имеем
. Имеем ,
, .
.


