
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Полная вероятность и формула БайесаСодержание книги
Поиск на нашем сайте
Решим задачу о Тезее, который, выбираясь из лабиринта, в пункте А потерял нить Ариадны. Какова вероятность того, что он придет в пункт В? Тезей случайным образом выходит на ту или иную дорогу, то есть событие В происходит с одним и только с одним из полной группы попарно несовместных событий

А1 А2 А3
ВА1 ВА2 ВА3
ВАn-2 ВАn-1 ВАn Аn-2 Аn-1 Аn
Применяя формулу для вероятности суммы несовместных событий, получим формулу полной вероятности.: Теорема гипотез Байеса. Пусть теперь известно, что событие В произошло. Тогда Требуется найти вероятности Из последнего равенства получим формулу Байеса Пример. Имеются 2 урны, в каждой из которых находится по 10 шаров, причем в 1-й урне 7 белых и 3 черных шара, во 2-й – 2 белых и 8 черных. наудачу из одной из урн вынимается шар. а) Найти вероятность того, что вынут белый шар. б) шар оказался белым. Найти вероятность того, что он вытянут из второй урны. а) Пусть В – вытягивание белого шара. А1 –выбор первой урны, А2 – выбор второй урны, Тогда Р(В) можно вычислить по формуле полной вероятности Пример. Мышка наугад выбирает одну из двух одинаковых кормушек, состоящих из пяти ячеек. В одной кормушке сыр только в одной ячейке, в другой – в четырёх. Событие А – съесть кусочек сыра. Какова вероятность события А? Каковы вероятности того, что второй раз мышка побежит к первой корзине, ко второй корзине? Рассмотрим гипотезы: Н1 – мышка бежит к первой кормушке, Н2 – мышка бежит ко второй кормушке. Р(Н1) =1/2 = Р(Н2) (априорные вероятности) Р(Н1/A) Р(Н2/A) При втором подходе Это – один из основных принципов обучения кибернетических систем. Схемы испытаний
Напомним, что опытом в теории вероятностей называют контролируемое осуществление некоторого комплекса условий S, которое можно повторить неограниченное число раз. Пусть производится n опытов (испытаний), в каждом из которых может наступить один из N исходов. Определение 1. Если результаты одного испытания не зависят от результатов других испытаний, то такие испытания называются независимыми. Пример. В урне 3 белых и 4 чёрных шара. Вынимают 2 шара по очереди. Событие А – вытащить 1й шар белый B и второй белый. Событие В – вытащить 2й шар белый. Покажем, что события А и В зависимы. Возможны две ситуации: условия проведения испытаний не меняются (ситуация А) или меняются от испытания к испытанию (ситуация В). Определение 2. Схема независимых испытаний с неизменными условиями и с двумя исходами в каждом из которых некоторое случайное событие А наступает с одной и той же вероятностью p = P(A), не изменяющейся от испытания к испытанию, называется схемой Бернулли. Схема Бернулли отвечает на следующие группы вопросов: I. Какова вероятность того, что в серии из Пример. Какова вероятность с пяти раз вытащить из колоды в 36 карт ровно три туза? Карты каждый раз возвращаются в колоду. Пример. Что вероятнее: выиграть у равносильного противника в шахматы 2 партии из трех или 3 партии из четырех? Р3(2)= Приближения. При большом числе n повторных испытаний использование формулы Бернулли затруднительно в связи с необходимостью выполнения действий над очень большими числами.
Случайные величины
Случайная величина – это величина (число), которая в результате опыта может принимать то или иное значение. Более строго, случайная величина – это числовая функция случайного события. Случайная величина называется дискретной, если множество ее значений конечно или счетно. Здесь Случайная величина называется непрерывной, если ее значения заполняют некоторый интервал, возможно, бесконечный. Здесь
Рассмотрим дискретную случайную величину, принимающую значения Законом распределения дискретной случайнойвеличины называется любое соотношение, устанавливающее зависимость между ее значениями Основные формы закона распределения дискретной случайной величины: ряд распределения – таблица
p3 p2 p1, pn x1 x2 x3 …xn Можно задать закон распределения в виде аналитической зависимости, связывающей значения Рассмотрим непрерывную случайную величину. Для непрерывной случайной величины Функцией распределения непрерывной случайной величины
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 395; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.007 с.) |

 . Они называются гипотезами. Известны вероятности этих событий
. Они называются гипотезами. Известны вероятности этих событий  . Но далее из каждого пункта он попадет в пункт В с различной вероятностью. Эти вероятности обозначим
. Но далее из каждого пункта он попадет в пункт В с различной вероятностью. Эти вероятности обозначим  , где i принимает значения от 1 до n. Требуется вычислить полную вероятность Р(В) того, что Тезей попадет из пyнкта А в пункт В. Другими словами, пусть требуется определить вероятность события В, которое может произойти в сочетании с одним из событий А1, А2,…, Аn, образующих полную группу несовместных событий (
, где i принимает значения от 1 до n. Требуется вычислить полную вероятность Р(В) того, что Тезей попадет из пyнкта А в пункт В. Другими словами, пусть требуется определить вероятность события В, которое может произойти в сочетании с одним из событий А1, А2,…, Аn, образующих полную группу несовместных событий (
 ,
,  ). Эти события будем называть гипотезами.
). Эти события будем называть гипотезами.




 . Вероятности
. Вероятности  называются априорными (a priori – (лат.) до того).
называются априорными (a priori – (лат.) до того). .
. i=l, 2,..., n - вероятности гипотез после опыта. Они называются апостериорными (a posteriori – (лат.) после того). Используя теорему умножения вероятностей, имеем P(ВАi) =
i=l, 2,..., n - вероятности гипотез после опыта. Они называются апостериорными (a posteriori – (лат.) после того). Используя теорему умножения вероятностей, имеем P(ВАi) = 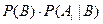
 , то есть
, то есть  . б). По формуле Байеса имеем
. б). По формуле Байеса имеем  , тогда
, тогда 
 .
. 

 (апостериорные вероятности).
(апостериорные вероятности).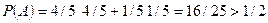 , то есть мышка обучилась, второй раз она выберет первую кормушку с большей вероятностью и добьется большего успеха.
, то есть мышка обучилась, второй раз она выберет первую кормушку с большей вероятностью и добьется большего успеха. ,
,  ,
,  .
.  независимых испытаний событие
независимых испытаний событие  появится ровно
появится ровно  раз. В этом случае любой исход n испытаний Бернулли представляет собой последовательность длины n, состоящую из k "успехов" и (n – k) "неуспехов". Вероятность каждого такого исхода по теореме умножения независимых случайных событий равна pk(1 - p)n-k или pkqn-k, где q=1 - p. Число таких комбинаций равно числу способов выбора k мест из n для "успеха". Тогда
раз. В этом случае любой исход n испытаний Бернулли представляет собой последовательность длины n, состоящую из k "успехов" и (n – k) "неуспехов". Вероятность каждого такого исхода по теореме умножения независимых случайных событий равна pk(1 - p)n-k или pkqn-k, где q=1 - p. Число таких комбинаций равно числу способов выбора k мест из n для "успеха". Тогда 
 формула Бернулли.
формула Бернулли.
 (1/2)2(1/2) = 3/8, Р4(3) =
(1/2)2(1/2) = 3/8, Р4(3) =  (1/2)3(1/2) = 1/4. То есть вероятнее выиграть 2 партии из трех.
(1/2)3(1/2) = 1/4. То есть вероятнее выиграть 2 партии из трех.
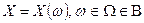
 - алгебра событий. Например, число очков на грани брошенной кости, число бросков монеты до появления герба – дискретные случайные величины.
- алгебра событий. Например, число очков на грани брошенной кости, число бросков монеты до появления герба – дискретные случайные величины.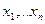 . Имеем полную группу (иначе, не все значения учтены) несовместных событий
. Имеем полную группу (иначе, не все значения учтены) несовместных событий  . Вероятности этих событий равны соответственно
. Вероятности этих событий равны соответственно 
 . Будем говорить, что дискретная случайная величина
. Будем говорить, что дискретная случайная величина  принимает значения
принимает значения 




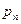

 многоугольник распределения
многоугольник распределения , поэтому рассматривают события
, поэтому рассматривают события  и вероятности этих событий.
и вероятности этих событий. называется вероятность события
называется вероятность события  .
.


