
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центральный момент s-го порядка
Для дискретной случайной величины Для непрерывной случайной величины
Дисперсией называется второй центральный момент случайной величины. По свойствам математического ожидания получим Для дискретных случайных величин Для непрерывных случайных величин Свойства дисперсии. 1) 2) 3) Средним квадратическим отклонением называется Кроме этих основных числовых характеристик используются коэффициент асимметрии Пример. Стрелок делает один выстрел и с вероятностью p попадает в мишень. Пусть X – количество попаданий в мишень. Это – дискретная случайная величина, принимающая два значения х1 = 0 и х2 = 1 с вероятностями q = 1-p, p соответственно. Построим ряд распределения Х
Функция распределения равна Математическое ожидание равно M(X) = mx = 0 q + 1 p = p. Если составить ряд распределения для случайной величины X2, то мы получим ту же таблицу (так как 02 = 0 и 12 =1). Поэтому M(X2) = p, а дисперсию можно вычислить по формуле D(X) = M(X2) – (mx)2 = p – p2 = p(1-p) = pq. Распределение называется равномерным на отрезке [a,b], еслиплотность случайной величины X постоянна на отрезке [a,b] p(x) = p и равна нулю вне этого отрезка. Из условия нормировки для плотности вероятности следует
= Повторные испытания. Пусть производится n опытов (испытаний), в каждом из которых может наступить один из N исходов. Если результаты одного испытания не зависят от результатов других испытаний, то такие испытания называются независимыми. Например, стрелок делает n выстрелов в мишень, в которой N колец: десятка, девятка и т.д. Возможны две ситуации: условия проведения испытаний не меняются (ситуация А) или меняются от испытания к испытанию (ситуация В). Рассмотрим ситуацию А. Пусть число исходов равно двум (N = 2). Схема независимых испытаний с двумя исходами называется схемой Бернулли. Два исхода соответствуют в приведенном примере попаданию (успеху) или не попаданию в мишень, причем в каждом выстреле вероятность попадания равна p, а вероятность промаха равна q = 1 – p. Обозначим вероятность попасть m раз из n выстрелов P(m,n).
Само распределение В самом деле, это – коэффициенты при производящей функции Из формулы Бернулли вытекают два следствия: 1) Вероятность появления успеха в n испытаниях не более m1 раз и не менее m2 раз равна 2) Вероятность хотя бы одного успеха в n испытаниях равна Если Х имеет биномиальное распределение, то Мх = np, Dx = npq. Пусть в ситуации А число исходов равно N, а их вероятности равны p1…pN. Вычислим вероятность того, что после n испытаний i – тый исход наступит
Заметим, что так как Поэтому Заметим, что Рассмотрим ситуацию В. Здесь вероятность того или иного исхода зависит от номера испытания, так как условия испытаний различны. При двух исходах
Примеры. 1) Какова вероятность с пяти раз вытащить из колоды в 36 карт а)три туза, б)не менее одного туза? а) 2) Мишень для опытного стрелка содержит три круговых кольца: 10, 9, пусто. Вероятность попасть при одном выстреле в десятку – 0,2, в девятку – 0,7, в «пусто» – 0,1. Какова вероятность в серии из 10 выстрелов попасть в «пусто» два раза, в девятку 4 раза, в десятку 4 раза?
3) Производится три выстрела в мишень. При первом выстреле вероятность попасть в мишень равна 0,5, не попасть 0.5. При втором выстреле – соответственно 0,4 и 0.6, при третьем выстреле 0,3 и 0,7. Какова вероятность два раза попасть в мишень?
Вероятность не попасть ни разу 0,21, один раз – 0,44, два раза – 0,29, три раза – 0,06.
|
||||||||||||
|
Последнее изменение этой страницы: 2017-02-05; просмотров: 325; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.0.61 (0.009 с.) |
 .
. .
. 

 . Эта формула часто применяется. Дисперсия – это характеристика рассеяния, она характеризует концентрацию кривой распределения (графика плотности распределения) около математического ожидания. Если на числовой оси расположить точки xi с массами pi, то дисперсия – это момент инерции системы материальных точек относительно центра тяжести mx.
. Эта формула часто применяется. Дисперсия – это характеристика рассеяния, она характеризует концентрацию кривой распределения (графика плотности распределения) около математического ожидания. Если на числовой оси расположить точки xi с массами pi, то дисперсия – это момент инерции системы материальных точек относительно центра тяжести mx.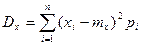 .
. .
. (под интегралом стоит квадрат функции).
(под интегралом стоит квадрат функции). (
( .
. (выведите сами, вынося
(выведите сами, вынося 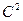 из под суммы или из под интеграла).
из под суммы или из под интеграла).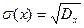 .
. , эксцесс – мера островершинности распределения
, эксцесс – мера островершинности распределения  , среднее арифметическое отклонение
, среднее арифметическое отклонение  , мода – наиболее вероятное значение для дискретных величин или значение, где плотность максимальна для непрерывных величин, медиана Me – абсцисса точки, в которой площадь, ограниченная кривой плотности распределения, делится пополам (точка, в которой F(x) = ½).
, мода – наиболее вероятное значение для дискретных величин или значение, где плотность максимальна для непрерывных величин, медиана Me – абсцисса точки, в которой площадь, ограниченная кривой плотности распределения, делится пополам (точка, в которой F(x) = ½). ,
, . Отсюда следует, что
. Отсюда следует, что  - плотность равномерного распределения. Функция распределения величины, распределенной равномерно на отрезке [a,b], равна
- плотность равномерного распределения. Функция распределения величины, распределенной равномерно на отрезке [a,b], равна . Вычислим математическое ожидание и дисперсию величины, распределенной равномерно на отрезке [a,b].
. Вычислим математическое ожидание и дисперсию величины, распределенной равномерно на отрезке [a,b]. ,
, =
= 

 , так как в каждом опыте стрелок промахивается. Вероятность попасть один раз равна
, так как в каждом опыте стрелок промахивается. Вероятность попасть один раз равна  , так как стрелок может попасть при первом, втором, … n ом выстреле.
, так как стрелок может попасть при первом, втором, … n ом выстреле.  ,так как два попадания (порядок не важен) должны быть размещены (выборки без возвращения) среди n выстрелов. Аналогично
,так как два попадания (порядок не важен) должны быть размещены (выборки без возвращения) среди n выстрелов. Аналогично - формула Бернулли.
- формула Бернулли. называют биномиальным.
называют биномиальным. в разложении по степеням
в разложении по степеням 
 .
. ,
,
 .
. раз
раз 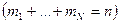
 .
. .
. .
. . Это – полиномиальное распределение.
. Это – полиномиальное распределение. - это коэффициенты при
- это коэффициенты при  в разложении по степеням
в разложении по степеням  производящей функции
производящей функции  .
.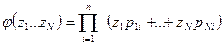 при N исходах.
при N исходах. - это коэффициент при
- это коэффициент при  , где
, где  .
. , б)
, б)  .
.
 .
.


