
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Гоморі розв’язування задач цілочислового програмуванняСодержание книги
Поиск на нашем сайте
Метод Гоморі є одним із методів відтинання. Суть методів відтинання полягає в тому, що розв’язується задача лінійного програмування без врахування цілочислової умови. Якщо розв’язок виявиться цілочисловим, то вихідна задача розв’язана. Якщо розв’язок – нецілочисловий, то до обмежень вихідної задачі додають додаткове лінійне обмеження і знову шукається розв’язок задачі за нових умов. Це нове обмеження задовольняє цілочислові розв’язки вихідної задачі, але не задовольняє отриманий нецілочисловий оптимальний розв’язок. Тому таке додаткове обмеження називається правильним обмеженням або відтинанням. Нові відтинання додають до обмежень вихідної задачі аж доки на деякому кроці не буде отримано цілочислового розв’язку. Розглянемо правила побудови нерівності Гоморі. Цілою частиною числа а називають найбільше ціле число, що менше або дорівнює йому (позначають [ a ]):
Дробовою частиною числа а називають різницю між числом а та його цілою частиною (позначають (f (а)):
Наприклад:
Очевидно,
причому
Ці властивості легко перевірити, наприклад:
Будь-який допустимий розв’язок канонічної задачі (4.1) – (4.3) лінійного програмування можна записати в такому вигляді
Цей розв’язок може бути ще й базисним, зокрема за умови
Для співвідношення (4.12) на основі властивості (4.10) функції f можемо записати
Припустимо, що (4.12) – цілочисловий допустимий розв’язок, тобто всі
і нерівність (4.14) приймає вигляд
Нерівність (4.16) називається правильним обмеженням або обмеженням (нерівністю) Гоморі. При розв’язанні цілочислової задачі нерівність Гоморі використовується в еквівалентній формі
Правильне обмеження задовольняє будь-яку цілочислову точку області допустимих значень. В той же час це обмеження не задовольняє допустимий базисний розв’язок (в тому числі і оптимальний), який не є цілочисловим. Дійсно, нехай (4.12) – базисний допустимий нецілочисловий розв’язок. Тоді права частина нерівності (4.16) Розглянемо приклади складання нерівності Гоморі.
матимемо
або
Приклад 2. Для рівності
матимемо
Приклад 3. Для рівності
матимемо
Приклад 4. Для рівності
матимемо
Якщо в процесі розв’язання цілочислової задачі на етапі складення нерівності Гоморі дістаємо абсурдний результат, як в прикладі 4, то це свідчить про відсутність цілочислового розв’язку. Для прикладу 4 абсурдний результат став наслідком того, що рівняння
Алгоритм методу Гоморі можна описати за допомого трьох кроків, що повторюються. Крок 1. Знаходимо розв’язок канонічної задачі лінійного програмування без умови цілочисловості. Якщо ця задача не має розв’язку, то і цілочислова задача також не має розв’язку. Крок 2. Якщо знайдений на першому кроці оптимальний план виявився цілочисловим, то задачу розв’язано. У протилежному разі вибираємо базисну змінну з найбільшою дробовою частиною і за обмеженням (4.12), записаним для цієї змінної складаємо нерівність Гоморі (4.16). Якщо отриманий результат – абсурдний, то цілочислова задача розв’язку не має. Крок 3. До обмежень задачі додаємо нерівність Гоморі в формі (4.17). Отримуємо розширену задачу і повертаємося до кроку 1.
Процес із зазначених трьох кроків повторюється аж поки не дістанемо цілочисловий розв’язок або виявимо, що задача не має розв’язку. Звернемо увагу: в записаному алгоритмі не указано яким методом знаходити розв’язок канонічної задачі лінійного програмування на першому кроці. Цей розв’язок можна шукати симплекс-методом. Але при цьому прийдеться виконувати досить громіздкі обчислення. Більш ефективним є наступний підхід. При першому виконанні кроку 1 застосовуємо симплекс-метод або двоїстий симплекс-метод, а на всіх інших ітераціях – двоїстий симплекс-метод. Справа в тому, що після додавання до системи обмежень нерівності Гоморі, оптимальний план, який було знайдено, стає псевдопланом нової задачі, до того ж, як правило, недалеко розташованим за кількістю ітерацій від оптимального плану. Тобто, застосування двоїстого симплекс-методу порівняно з симплекс-методом, дає в такій ситуації виграш не тільки в знаходженні початкового плану задачі, але й в кількості кроків при переході від початкового плану до оптимального. Зауваження. Перехід до канонічної форми в повністю цілочисловій задачі лінійного програмування, що записана в стандартній формі з обмеженнями – нерівностями
взагалі-то не приводить до повністю цілочислової задачі в канонічній формі, оскільки в перетворених обмеженнях (4.18)
додаткові змінні не підпорядковуються умові цілочисловості. Однак, якщо всі коефіцієнти Приклад 5. Знайти методом Гоморі розв’язок задачі
за умови
Розв’язання. Перетворимо нерівності системи обмежень в строгі рівності введенням додаткових невідомих
Всі коефіцієнти
Рисунок 4.4 – Областю допустимих значень нецілочислової задачі (a) – (c), є трикутник АВС, межа області допустимих значень цілочислової задачі (a) – (c) показана жирної лінією
Областю допустимих значень нецілочислової задачі є трикутник АВС. Рівняння кожної сторони трикутника наведено в таблиці 4.1.
Таблиця 4.1
В останньому стовпці таблиці указано додаткову змінну, яку вводили у відповідну нерівність при переході до канонічної форми вихідної задачі. Із графічного методу очевидно, що оптимальний план нецілочислової задачі відповідає т. С, яка є перетином прямих АС та ВС. Оскільки, згідно з таблицею 4.1, вздовж прямої АС змінна > z:=-2*x[1]-4*x[2]: Sys:={x[1]+3*x[2]+x[3]=12, 2*x[1]+x[2]-x[4]=6, 19*x[1]-8*x[2]+x[5]=57}: Sols_0:=solve(Sys, {x[k]$k=1..5} minus{x[3], x[4]});
Знайдемо значення базисних змінних в базисному розв’язку, для чого підставимо в загальний розв’язок нульові значення вільних невідомих > subs(x[3]=0, x[4]=0, Sols_0);
Серед базисних змінних відсутні від’ємні, отже, маємо початковий опорний план. Перевіримо його на оптимальність > ‘z’=subs(Sols_0, z);
Перед вільними змінними стоять коефіцієнти зі знаком “-”, отже при збільшенні цих змінних цільова функція буде зменшуватися, а це означає, що знайдений опорний план – оптимальний, як ми і передбачали. В знайденому плані компоненти x 1 та x 2 мають нецілочислові значення. При цьому дробові частини у них рівні. Складаємо додаткове обмеження на основі рівності для змінної x 2. Ця рівність є третім елементом множини Sols_0 > Sols_0[3];
Складемо правильне обмеження на основі цієї рівності
Зауваження. Обчислити дробову частину числа в Maple можна за допомогою простої процедури: > my_frac:=(x::numeric)->x-floor(x);
> my_frac(18/5);
Помножимо обидві частини нерівності на 5 та перетворимо її на рівність, ввівши додаткову змінну
і розв’язуємо задачу двоїстим симплекс-методом. В Maple додати рівність до системи рівнянь можна так > Sys1:=Sys union {2*x[3]+x[4]-x[6]=3};
Залишаючи ті ж самі вільні невідомі x 3, x 4, знаходимо загальний розв’язок, значення базисних невідомих та вираз цільової функції через вільні невідомі > Sols_1:=solve(Sys1, {x[k]$k=1..6}minus{x[3], x[4]});
> subs(x[3]=0, x[4]=0, Sols_1);
> ‘z’=subs(Sols_1, z);
Маємо псевдоплан – виконуються умови оптимальності, але не виконується умова невід’ємності: > Sols_1:=solve(Sys1, {x[k]$k=1..6}minus{x[3], x[6]});
> subs(x[3]=0, x[6]=0, Sols_1);
> ‘z’=subs(Sols_1, z);
Умова оптимальності не виконується, отже вибираємо за вільні > Sols_1:=solve(Sys1, {x[k]$k=1..6}minus{x[4], x[6]});
> subs(x[4]=0, x[6]=0, Sols_1);
> ‘z’=subs(Sols_1, z);
Виконуються і умова оптимальності і умова невід’ємності – маємо оптимальний план. Але цей план нецілочисловий. Згідно з кроком 2 алгоритму Гоморі вибираємо будь-яку з базисних змінних > Sols_1[3];
Складемо правильне обмеження на основі цієї рівності
Помножимо обидві частини нерівності на 2 та перетворимо її на рівність, ввівши додаткову змінну > Sys2:=Sys1union{x[4]+x[6]-x[7]=1};
знаходимо загальний розв’язок при тих самих вільних невідомих > Sols_2:=solve(Sys2, {x[k]$k=1..7}minus{x[4], x[6]});
значення базисних змінних > subs(x[4]=0, x[6]=0, Sols_2);
та вираження цільової функції через вільні невідомі > ‘z’=subs(Sols_2, z);
Маємо псевдоплан. Застосовуємо двоїстий симплекс-метод: замість вільної змінної > Sols_2_1:=solve(Sys2, {x[k]$k=1..7}minus{x[4], x[7]});
> subs(x[4]=0, x[7]=0, Sols_2_1);
> ‘z’=subs(Sols_2_1, z);
Отримали оптимальний план, який знову ж таки виявився нецілочисловим. Найбільша дробова частина у змінної > Sols_2_1[-2];
Складемо правильне обмеження на основі цієї рівності
Помножимо обидві частини нерівності на 5 та перетворимо її на рівність, ввівши додаткову змінну > Sys3:=Sys2 union {4*x[4]+x[7]-x[8]=4};
Знаходимо загальний розв’язок при тих самих вільних > Sols_3:=solve(Sys3, {x[k]$k=1..8}minus{x[4], x[7]});
значення базисних змінних > subs(x[4]=0, x[7]=0, Sols_3);
та вираження цільової функції через вільні невідомі > ‘z’=subs(Sols_3, z);
Маємо псевдоплан. Застосовуємо двоїстий симплекс-метод: замість вільної змінної x 4 вводимо змінну x 8: > Sols_3_1:=solve(Sys3, {x[k]$k=1..8}minus{x[7], x[8]});
> subs(x[7]=0, x[8]=0, Sols_3_1);
> ‘z’=subs(Sols_3_1, z);
Ми дістали оптимальний цілочисловий план, згідно з яким Оскільки вихідна задача є двовимірною ми можемо дати геометричну інтерпретацію процесу її розв’язання за методом Гоморі.
Перша нерівність Гоморі, яку ми долучили до системи обмежень (b) мала вигляд > Sols_1_1:=solve(Sys1, {x[k]$k=1..6}minus{x[1], x[2]});
Підставимо вирази для > 2*rhs(Sols_1_1[2])+rhs(Sols_1_1[1])>=3;
або Друга нерівність Гоморі, яку ми долучили до системи обмежень, мала вигляд > Sols_2_1:=solve(Sys2, {x[k]$k=1..7}minus{x[1], x[2]});
Підставимо вирази для > 1*rhs(Sols_2_1[1])+rhs(Sols_2_1[3])>=1;
або Третя нерівність Гоморі, яку ми долучили до системи обмежень мала вигляд > Sols_3_2:=solve(Sys3, {x[k]$k=1..8}minus{x[1], x[2]});
та запишемо цю нерівність через > 4*rhs(Sols_3_2[1])+rhs(Sols_3_2[-2])>=4;
або Розглянемо випадок, коли область допустимих значень не містить жодної цілочислової точки. Приклад 6. Знайти методом Гоморі розв’язок задачі
за умови
Розв’язання. Перетворимо нерівності системи обмежень в строгі рівності введенням додаткових невідомих
Оскільки вихідна задача двовимірна, ми можемо дати її геометричну інтерпретацію. Як видно із рис. 4.6, область допустимих значень не містить жодної цілочислової точки. Рівняння кожної сторони трикутника наведено в таблиці 4.2.
Рисунок 4.6 – Графічне зображення задачі (g) – (i): DАВС – область допустимих значень
Таблиця 4.2
В останньому стовпці таблиці указано додаткову змінну, яку вводили у відповідну нерівність при переході до канонічної форми вихідної задачі. Із графічного методу очевидно, що оптимальному плану нецілочислової задачі відповідає т. А, яка є перетином прямих АВ та АС. Оскільки згідно з таблицею 4.2, вздовж прямої АВ змінна > z:=-2*x[1]+4*x[2]: Sys:={x[1]+3*x[2]+x[3]=12, 2*x[1]+x[2]-x[4]=6, 2*x[1]-3*x[2]+x[5]=-6}: Sols_0:=solve(Sys, {x[k]$k=1..5}minus{x[3], x[4]});
Знайдемо значення базисних змінних в базисному розв’язку, для чого підставимо в загальний розв’язок нульові значення вільних невідомих
Серед базисних змінних відсутні від’ємні, отже, маємо початковий опорний план. Перевіримо його на оптимальність > ‘z’=subs(Sols_0, z);
Перед вільними змінними стоять коефіцієнти зі знаком “-”, отже, при збільшенні цих змінних цільова функція буде зменшуватися, а це означає, що знайдений опорний план – оптимальний. В знайденому плані всі базисні змінні > Sols_0[3];
Складемо правильне обмеження на основі цієї рівності
Помножимо обидві частини нерівності на 5 та перетворимо її на рівність, ввівши додаткову змінну
і розв’язуємо задачу двоїстим симплекс-методом: > Sys1:=Sys union {2*x[3]+x[4]-x[6]=3};
> subs(x[3]=0, x[4]=0, Sols_0);
>‘z’=subs(Sols_0, z);
Маємо псевдоплан – виконуються умови оптимальності, але не виконуються умови невід’ємності > Sols_1_1:=solve(Sys1, {x[k]$k=1..6}minus{x[4], x[6]});
> subs(x[4]=0,x[6]=0,Sols_1_1);
> ‘z’=subs(Sols_1_1, z);
Отримали оптимальний, але нецілочисловий план. Складаємо правильне обмеження для змінної > Sols_1_1[1];
Складемо правильне обмеження на основі цієї рівності
Помножимо обидві частини нерівності на 10 та перетворимо її на рівність, ввівши додаткову змінну > Sys2:=Sys1 union {5*x[4]+9*x[6]-x[7]=5};
> Sols_2:=solve(Sys2,{x[k]$k=1..7}minus{x[4], x[6]});
> subs(x[4]=0, x[6]=0, Sols_2);
> ‘z’=subs(Sols_2, z);
Маємо псевдоплан – виконуються умови оптимальності, але не виконуються умови невід’ємності > Sols_2_1:=solve(Sys2, {x[k]$k=1..7}minus{x[4], x[7]}): > subs(x[4]=0, x[7]=0, Sols_2_1);
> Sols_2_2:=solve(Sys2, {x[k]$k=1..7}minus{x[6], x[7]}): > subs(x[6]=0, x[7]=0, Sols_2_1);
Це означає, що в результаті долучення до вихідної системи обмежень (j) нерівностей Гоморі ми врешті решт отримали задачу з пустою областю допустимих значень. Отже, вихідна задача не має цілочислового розв’язку. Зауваження. Складанням екстракоротких Maple програм, що вміщаються в один рядок, можна суттєво спростити розв’язання задачі. Так, в прикладі 6 знаходиться загальний розв’язок > Sols_0:=solve(Sys, {x[k]$k=1..5}minus{x[3], x[4]});
Maple повертає результат роботи команди solve у вигляді множини елементів. Елементами є вирази базисних змінних через вільні. Порядок, в якому розташовані елементи множини Maple вибирає за своїми правилами і цей порядок змінюється випадковим чином. Нам же зручно аналізувати цей розв’язок, коли рівності розташовані в порядку зростання індексу базисної змінної. Такого сортування можна досягнути за допомого такого програмного коду > Sols_0:=sort([op(Sols_0)],(x,y)–evalb(op(lhs(x))<op(lhs(y))));
В результаті ми отримали загальний розв’язок у вигляді елементів списку (а не множини!), розташованих в порядку зростання номера індексу базисної змінної. Maple самостійно не змінює заданий порядок елементів списку, отже, значення базисних змінних в опорному розв’язку розташовані в тому ж самому порядку. Знайти дробові частини базисних змінних та розташувати їх в порядку зростання дробової частини допоможе такий програмний код > Sols_0:=subs(x[3]=0, x[4]=0, Sols_0);
> Sort(map(z->f(lhs(z))=my_frac(rhs(z)), Sols_0),(x,y)->evald(rhs(x)<rhs(y)));
Наведені в зауваженні приклади демонструють як потужну інтелектуальність Maple при розв’язуванні широкого кола питань, що виходять за рамки чисто математичних задач, так і те, що ефект від використання цієї системи зростає з ростом досвідченості користувача. Приклад 7. Знайти методом Гоморі розв’язок задачі
за умови
Розв’язання. Вибираючи за вільні змінні > z:=10*x[1]+x[2]: Sys:={3*x[1]+6*x[2]+6*x[3]=2}: Sols_0:=solve(Sys,{x[k]$k=1..3}minus{x[2], x[3]});
> subs(x[2]=0, x[3]=0, Sols_0);
> ‘z’=subs(Sols_0,z);
Отже, знайдений опорний план оптимальний, але нецілочисловий. Оскільки базисна змінна єдина – > my_frac:=(x::numeric)->x-floor(x): my_frac(2)*x[2]+my_frac(2)*x[3]>=my_frac(2/3);
На етапі складання нерівності Гоморі ми дістали неможливий результат: додатне число – менше нуля. Це свідчить про те, що задача не має цілочислових розв’язків. Якщо умова цілочисловості накладається не на всі змінні задачі лінійного програмування, то така задача називається частково цілочисловою. Для розв’язання таких задач також використовується метод Гоморі. Але в цьому випадку правильне обмеження, залишаючись схожим на (4.16), складається за дещо складнішими правилами
де 1) для
2) для
Зауваження. Кількість ітерацій в методі Гоморі суттєво залежить від того, наскільки вдало сформовано правильне відтинання. В практичних обчисленнях збіжність цього методу досить повільна.
|
|||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 448; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.36.215 (0.01 с.) |

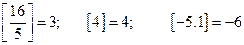
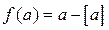 .
.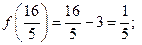

 .
.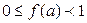 , (4.9)
, (4.9)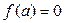 тоді й тільки тоді, коли а ціле число. У теорії чисел для дробової частини числа виводять такі дві властивості:
тоді й тільки тоді, коли а ціле число. У теорії чисел для дробової частини числа виводять такі дві властивості: , (4.10)
, (4.10)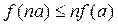 ,
, 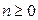 – ціле число. (4.11)
– ціле число. (4.11) ;
; 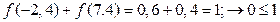 .
. ,
, 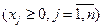 . (4.12)
. (4.12)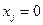 ,
,  . (4.13)
. (4.13) . (4.14)
. (4.14)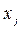 – цілі невід’ємні числа
– цілі невід’ємні числа  ). Тоді
). Тоді  , крім того на основі властивості (4.11) матимемо
, крім того на основі властивості (4.11) матимемо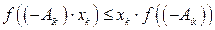 , (4.15)
, (4.15) . (4.16)
. (4.16) ,
, 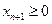 . (4.17)
. (4.17) , а з іншого боку з урахуванням (4.13) ліва частина нерівності дорівнює нулю. В результаті виходить, що нуль менший додатного числа, тобто нерівність не справджується. Отже, доручення до вихідних обмежень (4.2) правильного обмеження означає відтинання від області допустимих значень деякої її частини, яка містить оптимальний нецілочисловий розв’язок задачі (4.1) – (4.3) (він же базисний допустимий) і не містить жодного цілочислового допустимого розв’язку. В цьому і полягає основна ідея методів відтинання.
, а з іншого боку з урахуванням (4.13) ліва частина нерівності дорівнює нулю. В результаті виходить, що нуль менший додатного числа, тобто нерівність не справджується. Отже, доручення до вихідних обмежень (4.2) правильного обмеження означає відтинання від області допустимих значень деякої її частини, яка містить оптимальний нецілочисловий розв’язок задачі (4.1) – (4.3) (він же базисний допустимий) і не містить жодного цілочислового допустимого розв’язку. В цьому і полягає основна ідея методів відтинання.

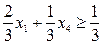 , →
, →  .
.
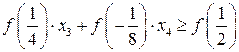
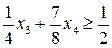 , →
, → 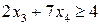 .
.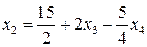
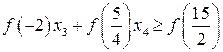
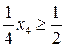 , →
, → 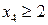 .
.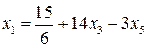
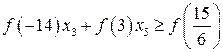
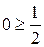 , → абсурдний результат.
, → абсурдний результат.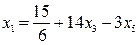 не має цілочислових розв’язків. Подібна ситуація виникає, коли в рівності (4.12) для нецілочислової базисної змінної всі коефіцієнти при вільних невідомих є цілими числами.
не має цілочислових розв’язків. Подібна ситуація виникає, коли в рівності (4.12) для нецілочислової базисної змінної всі коефіцієнти при вільних невідомих є цілими числами.
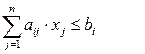 (4.18)
(4.18)
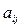 ,
, 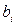 в (4.18) – цілі числа, то умову цілочисловості можна розповсюдити і на
в (4.18) – цілі числа, то умову цілочисловості можна розповсюдити і на 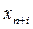 . Повністю цілочислову задачу в канонічній формі можна отримати також, якщо в (4.18)
. Повністю цілочислову задачу в канонічній формі можна отримати також, якщо в (4.18) 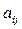 ,
,  ,
,  .
.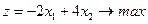 (a)
(a)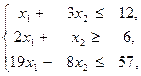 (b)
(b)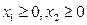 і цілі числа. (c)
і цілі числа. (c)
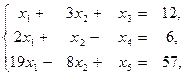 (d)
(d) , (e)
, (e)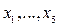 – цілі. (f)
– цілі. (f)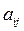 ,
,  Оскільки вихідна задача двовимірна, ми можемо дати її геометричну інтерпретацію.
Оскільки вихідна задача двовимірна, ми можемо дати її геометричну інтерпретацію.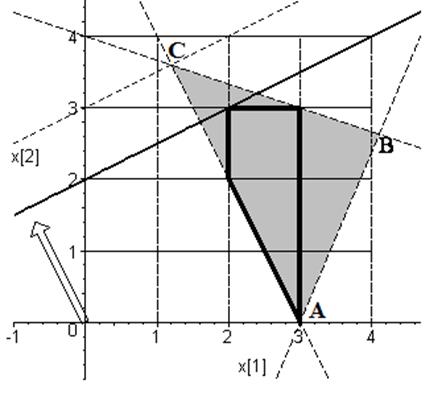

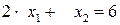

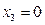 , а вздовж прямої
, а вздовж прямої 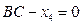 , вибираючи за вільні змінні
, вибираючи за вільні змінні 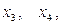 дістанемо опорний початковий розв’язок, який є оптимальним для нецілочислової задачі. Дійсно, знайдемо за допомогою Maple загальний розв’язок системи (d):
дістанемо опорний початковий розв’язок, який є оптимальним для нецілочислової задачі. Дійсно, знайдемо за допомогою Maple загальний розв’язок системи (d):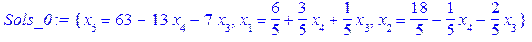 .
.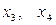
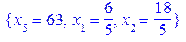 .
.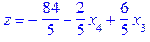 .
.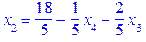 .
.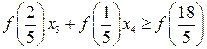
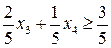 .
.
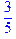 .
.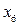 :
: 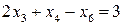 . Додаємо це обмеження до вихідної системи (d)
. Додаємо це обмеження до вихідної системи (d)
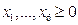 і цілі, (d1)
і цілі, (d1)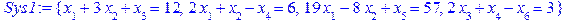
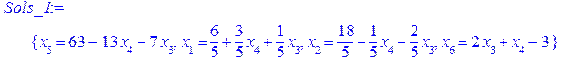
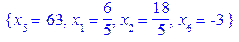
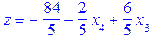 .
. . Замість одної з вільних невідомих
. Замість одної з вільних невідомих 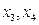 потрібно ввести в вільну змінну
потрібно ввести в вільну змінну 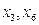

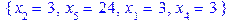
 .
.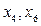 :
: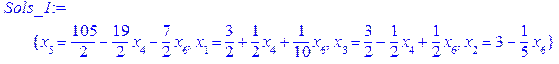

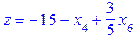 .
. , що мають дробові значення. Складемо нерівність Гоморі на основі обмеження для змінної
, що мають дробові значення. Складемо нерівність Гоморі на основі обмеження для змінної  . Рівність для цієї змінної є третім елементом в множині Sols_1
. Рівність для цієї змінної є третім елементом в множині Sols_1 .
.
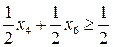 .
.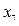 :
: 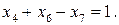 Додаємо це обмеження до системи (d1)
Додаємо це обмеження до системи (d1) (d2)
(d2) і цілі числа,
і цілі числа,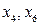

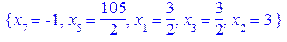
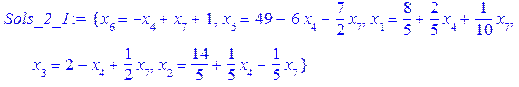
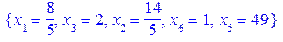 ,
, .
.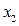 , отже будуємо нерівність Гоморі для відповідної рівності (в Maple для нумерації елементів множини з кінця потрібно використовувати індекс зі знаком “-“, оскільки рівність для
, отже будуємо нерівність Гоморі для відповідної рівності (в Maple для нумерації елементів множини з кінця потрібно використовувати індекс зі знаком “-“, оскільки рівність для 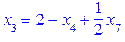 .
.
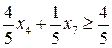 .
. :
: 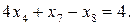 Додаємо це обмеження до системи (d2)
Додаємо це обмеження до системи (d2) (d3)
(d3)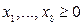 і цілі числа.
і цілі числа.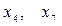 невідомих
невідомих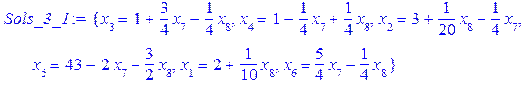
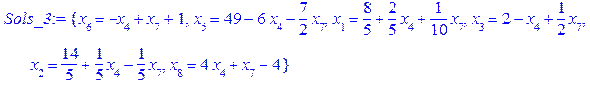
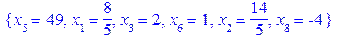
 ,
, .
. Цей результат випливає із даних, наведених на рис. 4.4.
Цей результат випливає із даних, наведених на рис. 4.4.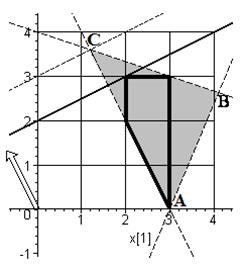

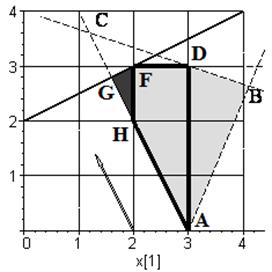

 відтинається D EFG
відтинається D EFG
 відтинається D FGH
відтинається D FGH
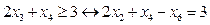 . Розв’яжемо систему (d1) відносно
. Розв’яжемо систему (d1) відносно 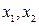 . Звісно, зробимо це за допомогою Maple
. Звісно, зробимо це за допомогою Maple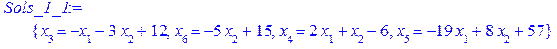
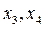 в нерівність Гоморі
в нерівність Гоморі 

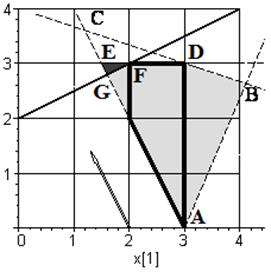
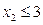 . Як змінюється область допустимих значень нецілочислової задачі в результаті долучення цієї нерівності видно із порівняння рис. 4.5 а та рис. 4. 5 б. від D АВС відітнули D CDE і отримали многокутник ABDE.
. Як змінюється область допустимих значень нецілочислової задачі в результаті долучення цієї нерівності видно із порівняння рис. 4.5 а та рис. 4. 5 б. від D АВС відітнули D CDE і отримали многокутник ABDE.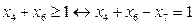 . Розв’яжемо відповідну систему відносно змінних
. Розв’яжемо відповідну систему відносно змінних 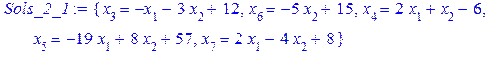
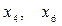 в нерівність Гоморі
в нерівність Гоморі 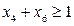

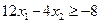 . Звернемо увагу, що в даному випадку опорна лінія співпадає з межею FG многокутника допустимих значень ABDFG (рис. 4.5, в), яка визначається рівнянням прямої
. Звернемо увагу, що в даному випадку опорна лінія співпадає з межею FG многокутника допустимих значень ABDFG (рис. 4.5, в), яка визначається рівнянням прямої 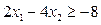 . Тобто, в цьому випадку оптимальному плану нецілочислової задачі відповідає будь-яка точка відрізка FG. Причому точка F (2; 3) є цілочисловою, точкою. Але, застосовуючи двоїстий симплекс-метод, ми вибрали із двох можливих варіантів перехід до т.
. Тобто, в цьому випадку оптимальному плану нецілочислової задачі відповідає будь-яка точка відрізка FG. Причому точка F (2; 3) є цілочисловою, точкою. Але, застосовуючи двоїстий симплекс-метод, ми вибрали із двох можливих варіантів перехід до т. 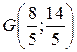 , а не до т. F (2; 3). Саме тому ми вимушені були зробити ще одну ітерацію алгоритму Гоморі. Перехід до т.
, а не до т. F (2; 3). Саме тому ми вимушені були зробити ще одну ітерацію алгоритму Гоморі. Перехід до т.  ввели замість змінної
ввели замість змінної  , то одержали б оптимальний план цілочислової задачі, що відповідає т. F (2; 3).
, то одержали б оптимальний план цілочислової задачі, що відповідає т. F (2; 3).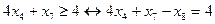 . Розв’яжемо відповідну систему відносно
. Розв’яжемо відповідну систему відносно 
 , дістанемо
, дістанемо
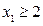 . В результаті долучення до системи обмежень останньої нерівності оптимальному плану відповідає цілочислова т. F (2; 3) на рис. 4.5 г.
. В результаті долучення до системи обмежень останньої нерівності оптимальному плану відповідає цілочислова т. F (2; 3) на рис. 4.5 г.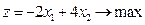 (g)
(g)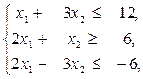 (h)
(h)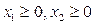 і цілі числа. (i)
і цілі числа. (i)
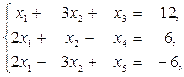 (j)
(j) , (k)
, (k)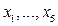 ‑ цілі. (l)
‑ цілі. (l)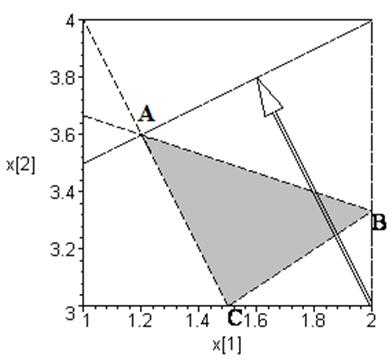

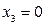 , а вздовж прямої
, а вздовж прямої  , вибираючи за вільні змінні
, вибираючи за вільні змінні 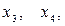 дістанемо опорний початковий розв’язок, який є оптимальним для нецілочислової задачі. Дійсно, знайдемо за допомогою Maple загальний розв’язок системи (j):
дістанемо опорний початковий розв’язок, який є оптимальним для нецілочислової задачі. Дійсно, знайдемо за допомогою Maple загальний розв’язок системи (j):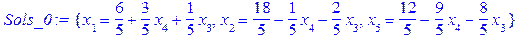 .
.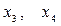
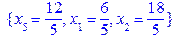 .
.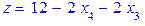 .
. мають нецілочислові значення. При цьому дробова частина найбільша для змінної
мають нецілочислові значення. При цьому дробова частина найбільша для змінної 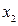 . Складаємо додаткове обмеження на основі рівності для цієї змінної:
. Складаємо додаткове обмеження на основі рівності для цієї змінної: .
.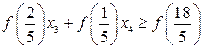 ,
,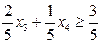 .
. . Додаємо це обмеження до вихідної системи (j)
. Додаємо це обмеження до вихідної системи (j)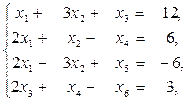
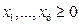 і цілі числа (j1)
і цілі числа (j1)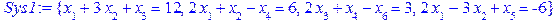 ,
,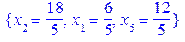 ,
, . Вводимо в вільні змінну
. Вводимо в вільні змінну 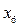 замість
замість  , матимемо
, матимемо ,
, ,
, .
.
 .
.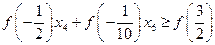 ,
,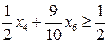 .
.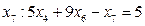 . Додаємо це обмеження до вихідної системи (j1)
. Додаємо це обмеження до вихідної системи (j1)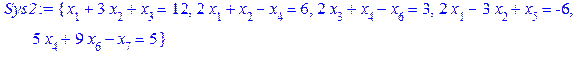
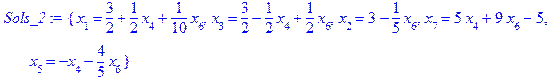
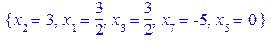
 .
. . Оскільки в даній задачі тільки дві вільні змінні, то перехід від поточного псевдоплану до оптимального можливий одним із двох варіантів – вибором як вільні
. Оскільки в даній задачі тільки дві вільні змінні, то перехід від поточного псевдоплану до оптимального можливий одним із двох варіантів – вибором як вільні 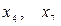 або
або  Обидва варіанти приводять до недопустимих розв’язків. Дійсно
Обидва варіанти приводять до недопустимих розв’язків. Дійсно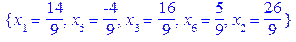
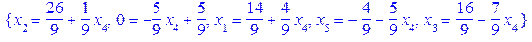 .
. .
.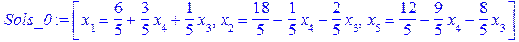 .
.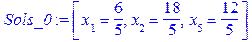
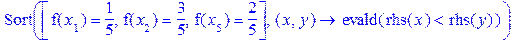
 (m)
(m) , (n)
, (n)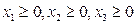 та цілі. (o)
та цілі. (o) дістанемо опорний початковий розв’язок, який є оптимальним для нецілочислової задачі. Упевнимося в цьому за допомогою Maple:
дістанемо опорний початковий розв’язок, який є оптимальним для нецілочислової задачі. Упевнимося в цьому за допомогою Maple: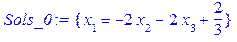
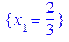
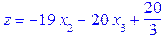 .
. , то нерівність Гоморі складатимемо для неї на основі виразу із розв’язку Sols_0:
, то нерівність Гоморі складатимемо для неї на основі виразу із розв’язку Sols_0: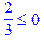 .
. , (4.19)
, (4.19) визначаються із таких співвідношень:
визначаються із таких співвідношень: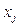 , які можуть приймати нецілочислові значення
, які можуть приймати нецілочислові значення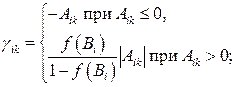 (4.20)
(4.20) , які можуть приймати тільки цілочислові значення
, які можуть приймати тільки цілочислові значення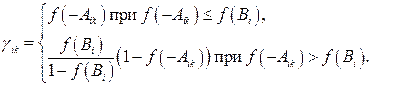 (4.21)
(4.21)


