
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні властивості та теореми двоїстостіСодержание книги
Поиск на нашем сайте Властивості допустимих розв’язків двоїстих задач сформулюємо як теореми двоїстості.
Властивість 1. (Основна нерівність теорії двоїстості) Якщо Доведення. Помножимо обмеження (2.9) на відповідні двоїсті невідомі
Знак нерівності не змінюється, оскільки всі
Аналогічні операції проведемо з обмеженнями(2.12):
Подвійні суми в нерівностях (2.20) і (2.21) являють собою різні форми запису одного й того самого виразу
отже, ці нерівності можна об’єднати
Остаточно основна нерівність теорії двоїстості для значень цільових функцій на допустимих розв’язках матиме вигляд
Властивість 2. Якщо Доведення. Будемо доводити властивість від супротивного. Припустимо існує оптимальний розв’язок прямої задачі Теорема 1. (Перша теорема двоїстості – теорема про мінімакс). Якщоодна з двоїстих задач має розв’язок, то інша також має розв’язок, і оптимальні значення цільових функцій на розв’язках цих задач однакові, тобто
Якщо одна з двоїстих задач не має розв’язку через те, що цільова функція не обмежена, то інша двоїста задача взагалі не має допустимих розв’язків. Наслідок. Для того щоб обидві взаємно двоїсті задачі мали розв’язок необхідно і достатньо, щоб кожна з них мала принаймні по одному допустимому розв’язку. Теорема 2. (Друга теорема двоїстості – двоїстий критерій оптимальності). Допустимі розв’язки
Якщо розглядається пара симетричних двоїстих задач (2.8) – (2.10) та (2.11) – (2.13), то повинні виконуватися ще і рівності
Рівності (2.24), (2.25) називають умовами доповняльної нежорсткості. Із цих рівностей випливає, що коли деяке обмеження задачі на оптимальному розв’язку не перетворюється на точну рівність, то відповідна невідома оптимального розв’язку двоїстої задачі обов’язково дорівнює нулю. Далі буде показано, як за допомогою наведених рівностей на основі відомого розв’язку задачі лінійного програмування можна знайти оптимальний розв’язок двоїстої задачі.
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 і
і  – допустимі розв’язки прямої (2.8) – (2.10) і двоїстої (2.11) – (2.13) задач, то
– допустимі розв’язки прямої (2.8) – (2.10) і двоїстої (2.11) – (2.13) задач, то  .
. , дістанемо
, дістанемо ,
,  . (2.19)
. (2.19) . Додамо ліві і праві частини нерівностей (2.19):
. Додамо ліві і праві частини нерівностей (2.19): (2.20)
(2.20) (2.21)
(2.21) ,
, .
. . (2.22)
. (2.22) і
і  – допустимі розв’язки взаємно двоїстих задач (2.8) – (2.10) та (2.11) – (2.13) і
– допустимі розв’язки взаємно двоїстих задач (2.8) – (2.10) та (2.11) – (2.13) і  , то
, то  – оптимальні розв’язки цих задач.
– оптимальні розв’язки цих задач. , для якого
, для якого  . Але тоді повинна справджуватися нерівність
. Але тоді повинна справджуватися нерівність  , що суперечить основній нерівності теорії двоїстості (2.22). Отже вихідне припущення – хибне, тобто для будь-якого допустимого, в тому числі й опорного розв’язку
, що суперечить основній нерівності теорії двоїстості (2.22). Отже вихідне припущення – хибне, тобто для будь-якого допустимого, в тому числі й опорного розв’язку  задачі (2.8) – (2.10) справедливо
задачі (2.8) – (2.10) справедливо  , а це і означає, що
, а це і означає, що 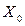 є оптимальним розв’язком прямої задачі. Аналогічно можна довести, що
є оптимальним розв’язком прямої задачі. Аналогічно можна довести, що 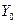 – оптимальний план двоїстої задачі (2.11) – (2.13).
– оптимальний план двоїстої задачі (2.11) – (2.13). (2.23)
(2.23)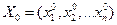 і
і  двоїстих задач відповідно (2.14) – (2.16) та (2.17) – (2.18) тоді і тільки тоді є оптимальними розв’язками цих задач, коли виконуються рівності
двоїстих задач відповідно (2.14) – (2.16) та (2.17) – (2.18) тоді і тільки тоді є оптимальними розв’язками цих задач, коли виконуються рівності
 (2.24)
(2.24)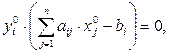
 (2.25)
(2.25)


