
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правило 2 (побудови взаємно-двоїстих задач)Содержание книги
Поиск на нашем сайте
1. Кількість змінних однієї задачі дорівнює загальній кількості рівнянь та нерівностей в системі обмежень іншої. 2. Коефіцієнти цільової функції однієї задачі дорівнюють правим частинам системи обмежень іншої. 3. Одна задача повинна бути на знаходження найбільшого, а інша – найменшого значення цільової функції. 4. Обмеження в задачі “на максимум” повинні бути записані за допомогою рівнянь і (або) нерівностей типу “£”, а в задачі “на мінімум” – за допомогою рівнянь і (або) нерівностей типу “³”. 5. Кожній нерівності системи обмежень однієї задачі повинна відповідати в іншій задачі невід’ємна змінна, а кожному рівнянню - повинна відповідати в іншій задачі змінна, на знак якої не накладено обмежень. 6. Матриця системи обмежень одної задачі повинна бути транспонованою матрицею системи обмежень іншої. Зокрема, якщо пряма задача задана в канонічній формі, то матимемо пару двоїстих задач в несиметричній формі:
Оскільки обмеження прямої задачі задані у вигляді рівностей, то на змінні двоїстої задачі не накладаються умови невід’ємності. Приклад 2 Скласти задачу двоїсту до задачі
Розв’язання. Щоб домогтися виконання п. 4 правила 2 помножимо обидві частини першої нерівності в системі обмежень (b) на (-1)
Складемо задачу, двоїсту до задачі (a), (d), (c). Обмеження прямої задачі (d) складаються з трьох співвідношень, отже, згідно з п. 1 правила 2, двоїста задача матиме три змінні
Згідно з п. 6 правила 2 коефіцієнти при невідомих в лівих частинах обмежень двоїстої задачі отримуються транспонуванням матриці коефіцієнтів при змінних в обмеженнях (d). Наприклад, в обмеження прямої задачі (d) змінна
Знак нерівності – “≤“ для першої та четвертої нерівностей і знак “=“ для другого та третього рівняння встановлюється згідно з п. 5 правила 2, а згідно з п. 2 правила 2 вільні члени дорівнюють коефіцієнтам цільової функції прямої задачі. Згідно з п. 5 правила 2 записуємо умову невід’ємності невідомих
Задачі (a), (d), (c) та (e), (f), (g) є взаємно-двоїстими. Якщо за вихідну взяти задачу (e), (f), (g) та побудувати двоїсту до неї, то отримаємо задачу (a), (d), (c). Двоїсті невідомі Кожна із пари двоїстих задач є самостійною задачею лінійного програмування і може бути розв’язана незалежно одна від одної. Але розв’язки цих задач тісно пов’язані. Щоб знайти ці зв’язки розглянемо основні властивості та теореми двоїстості.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 167; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.109.195 (0.009 с.) |

 (2.14)
(2.14) ,
, 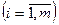 , (2.15)
, (2.15)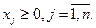 (2.16)
(2.16) (2.17)
(2.17) ,
,  (2.18)
(2.18)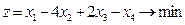 (a)
(a) , (b)
, (b) (c)
(c) , (d)
, (d) Згідно з п. 2 правила 2 коефіцієнти цільової функції двоїстої задачі дорівнюють вільним членам обмежень (d), а згідно з п. 3 правила 2– знаходиться найбільше значення цільової функції
Згідно з п. 2 правила 2 коефіцієнти цільової функції двоїстої задачі дорівнюють вільним членам обмежень (d), а згідно з п. 3 правила 2– знаходиться найбільше значення цільової функції (e)
(e) входить з такими коефіцієнтами (-2; -1; 2), отже, ці числа використовуємо як коефіцієнти лівої частини третьої нерівності двоїстої задачі
входить з такими коефіцієнтами (-2; -1; 2), отже, ці числа використовуємо як коефіцієнти лівої частини третьої нерівності двоїстої задачі , (f)
, (f)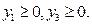 (g)
(g) називають внутрішніми або тіньовими цінами; вони дають змогу оцінити вартість використовуваних ресурсів, а тому їх називають також оцінками ресурсів.
називають внутрішніми або тіньовими цінами; вони дають змогу оцінити вартість використовуваних ресурсів, а тому їх називають також оцінками ресурсів.


