
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зв’язок між розв’язками прямої і двоїстої задач лінійного програмування
Перша та друга теореми двоїстості дають змогу за розв’язком однієї з двоїстих задач знайти розв’язок іншої. Запишемо співвідношення канонічної задачі лінійного програмування та двоїстої до неї у матричному вигляді: пряма задача
двоїста задача
де
Якщо задача лінійного програмування розв’язується симплекс-методом, то розв’язок
де
Приклад 5. Дана задача лінійного програмування
Потрібно: 1) знайти симплекс-методом розв’язок даної задачі; 2) скласти двоїсту задачу до заданої; 3) знайти симплекс-методом розв’язок двоїстої задачі; 4) знайти розв’язок двоїстої задачі за співвідношенням (2.31) та порівняти з розв’язком, знайденим симплекс-методом. Розв’язання. 1. Ввівши додаткові невідомі запишемо всі обмеження прямої задачі у вигляді строгих рівностей
Розв’язок даної задачі шукатимемо за допомогою Maple. За вільні виберемо змінні x 3, x 6: > z:=10*x[1]–x[2]–42*x[3]–52*x[4]: Sys:={- 3*x[1] + x[2]+4*x[3]+x[4]+x[5] = 1, 3*x[1]–2*x[2]+2*x[3]–2*x[4]+x[6] = -9, - 2*x[1]+x[2]+x[3]+3*x[4] = 2, - 3*x[1]+2*x[2]–3*x[3] = 7}: sols1:=solve (Sys, {x[1], x[2], x[4], x[5]});
Знайдемо значення базисних змінних > subs(x[3]=0, x[6]=0, %);
Від’ємні значення невідомих відсутні, отже, знайдений базисний розв’язок – допустимий. Перевіримо його на оптимальність > ‘z’=subs(%%, z);
Збільшення будь-якої з вільних невідомих –
причому
2. Складемо задачу, двоїсту до заданої задачі (2.32) – (2.34):
3. Знайдемо симплекс-методом розв’язок двоїстої задачі (2.38) – (2.40). Перш за все зведемо двоїсту задачу до канонічного вигляду. За правилом переходу до двоїстої задачі на змінні
Крім цього перетворимо нерівності системи обмежень (2.39) на строгі рівності, дістанемо
Оскільки ліві частини нерівностей (2.39) не менші правих частин, то від лівих частин відняли невід’ємні додаткові невідомі В Maple вказані дії зручно реалізувати в такій послідовності. Запишемо цільову функцію (2.38) та систему обмежень (2.39) > F:=y[1]–9*y[2]+2*y[3]+7*y[4]: Sys0:=[–3*y[1]+3*y[2]–2*y[3]–3*y[4]>=10, y[1]-2*y[2]+y[3]+2*y[4]>= -1, 4*y[1]+2*y[2]+y[3]–3*y[4]>=-42, y[1]-2*y[2]+3*y[3]>= -52];
Введенням додаткових змінних перетворимо нерівності на строгі рівності > Sys1:=[-3*y[1]+3*y[2]–2*y[3]–3*y[4]=10, y[1]–2*y[2]+y[3]+2*y[4]=-1, 4*y[1]+2*y[2]+y[3]–3*y[4]=-42, y[1]–2*y[2]+3*y[3]=-52];
Подамо змінні > y[3]:=y1[3]-y2[3]:y[4]:y1[4]-y2[4]: Sys1;
Всього рівнянь 4, змінних – 10, отже, для знаходження базисного розв’язку 10 – 4 = 6 змінних потрібно вибрати за вільні. Вибираємо за вільні > sols1:=solve (convert (Sys1, set),{y[2], y2[3], y1[4], y[7]});
Цей розв’язок виявляється не тільки допустимий, що легко перевірити за допомогою команди, > subs(y[1]=0, [3]=0, y2[4]=0, y[5]=0, y[6]=0, y[8]=0, sols1);
але й оптимальним. Дійсно, виразимо цільову функцію через вільні невідомі > ‘F’=subs(sols1, F);
Збільшення будь-якої вільної невідомої не може зменшити значення цільової функції, отже, Отже, оптимальним є такий розв’язок
або з урахуванням співвідношень (2.41)
Потрібно зауважити, що при знаходженні оптимального плану двоїстої задачі симплекс-методом ми зразу вгадали його, вибравши певні невідомі за вільні. На практиці розв’язання подібних задач, як правило, пов’язано з необхідністю виконання значної кількості повторень окремих кроків симплекс-алгоритму. 4. Знайдемо розв’язок двоїстої задачі за співвідношенням (2.31). Оптимальному розв’язку (2.36) прямої задачі відповідають такі базисні змінні:
> C[b]:=matrix([[10, -1, -52, 0]]): Створимо матрицю з коефіцієнтів системи (2.35) при базисних змінних > A[b]:=matrix([[-3, 1, 1, 1], [3, -2, -2, 0], [-2, 1, 3,0], [-3, 2, 0, 0]]);
Знайдемо матрицю, обернену до створеної матриці > A_1[b]:=linalg[inverse](A[b]): Оскільки елементи цієї матриці нас не цікавлять, результат операції присвоюється Maple-змінній A_1[b], але на екран монітора не виводиться. Залишилося знайти оптимальний розв’язок двоїстої задачі множенням двох матриць > Y[0]=evalm(C[b]&*A_1[b]);
Отриманий розв’язок є тотожним розв’язку (2.45), якщо із останнього вилучити додаткові (допоміжні) змінні Отже, якщо симплекс-методом знайдено розв’язок одної із пари двоїстих задач, то розв’язок іншої може бути легко знайдений за співвідношенням (2.31), що незрівнянно простіше в порівняні з розв’язанням двоїстої задачі як окремої задачі лінійного програмування. За розв’язком одної з двоїстих задач розв’язок іншої можна також знайти за допомогою першої та другої теорем двоїстості. Приклад 6. За допомогою другої та першої теорем двоїстості знайти розв’язок двоїстої задачі (2.38) – (2.40) із прикладу 5, якщо відомий розв’язок (2.36) прямої задачі (2.32) – (2.34). Розв’язання. За першою теоремою двоїстості Fmin = zmax = 21. В оптимальному розв’язку (2.36) прямої задачі відмінними від нуля є змінні
До цих трьох рівнянь додаємо четверте – завдяки відомому оптимальному значенні цільової функції (2.38)
Для знаходження оптимального розв’язку двоїстої задачі залишилося розв’язати сформовану систему чотирьох лінійних рівнянь: > System:=[-3*y[1]+3*y[2]-2*y[3]-3*y[4]=10, y[1]-2*y[2]+y[3]+2*y[4]=-1, y[1]-2*y[2]+3*y[3]=-52, y[1]-9*y[2]+2*y[3]+7*y[4]=21]: Y[0]=solve(convert(System, set));
Очевидно, що отримано той самий розв’язок, що і в прикладі 5, за допомогою співвідношення (2.31). Першою та другою теоремами двоїстості можна користуватися для знаходження розв’язку двоїстої задачі і у випадку, коли пряма задача розв’язана геометричним методом, а отже, співвідношенням (2.31) скористатися неможливо. ДВОЇСТИЙ СИМПЛЕКС-МЕТОД
Викладемо двоїстий симплекс-метод, не зупиняючись на його детальному обґрунтуванні. Розглянемо задачу лінійного програмування в канонічній формі
Розглянемо наступну задачу (розділ 2)
для та її графічне зображення, що показано на рис. 3.1. Введенням додаткових невідомих перетворимо нерівності системи обмежень (3.5) на строгі рівності
Рівняння кожної з прямих, що відповідають обмеженням задачі та зображені на рис. 3.1, наведені в таблиці 3.1.
Таблиця 3.1
Згідно із симплекс-методом спочатку знаходиться початковий опорний план – базисний допустимий розв’язок. Якщо початковий опорний план шукається методом вибору вільних змінних, то потрібно так вибрати вільні змінні, щоб отриманий базисний розв’язок виявився допустимим. Так, вибравши за вільні, наприклад, змінні
Всі точки, що позначені буквами на рис. 3.1. відповідають базисним розв’язкам. Причому т. O, A, B, C відповідають опорним планам - базисним допустимим розв’язкам, а решта точок – базисним недопустимим розв’язкам. Тобто, в розв’язках, що відповідають т. D, E, F,… – серед базисних змінних обов’язково знайдеться принаймні одна від’ємна. Для прикладу знайдемо розв’язки, що відповідають т. H і Q. Перша точка є перетином прямих DH і QH, друга точка – перетином прямих FQ і HQ. Отже, в одному випадку за вільні, згідно з таблицею 3.1, потрібно взяти змінні
Рисунок 3.1 – Графічне зображення задачі (3.4) – (3.6): OABC – многокутник допустимих значень; D(-1, 7), E(0, 7), F(0, 8), G(1/2, 7), H(5, 7), K(5, 1), L(6,0), P(5, 0), Q(5, -2) – точки, що відповідають базисним недопустимим розв’язкам; - - - опорна лінія в крайньому положенні. Згідно з двоїстим симплекс-методом початковим розв’язком також повинен бути базисний розв’язок. Але такий базисний розв’язок, для якого умови допустимості не виконуються, але обов’язково повинні виконуватися умови оптимальності. Базисний розв’язок, для якого виконуються умови оптимальності, але не виконуються умови допустимості називається псевдопланом
Знайдемо відповідні розв’язки за допомогою Maple. > eq1:=2*x[1]+x[2]+x[3]=8: eq2:=1*x[1]+x[2]+x[4]=6: eq3:=1*x[1]+x[5]=5: eq4:=1*x[2]+x[6]=7: Vilni:=x[5], x[6]; sols1:=solve({seq(eq||kk, kk=1..4)}, {seq(x[kk], kk=1..6)} minus {Vilni}); map(zz->zz=0, {Vilni}); subs(%, sols1);
Як видно, в розв’язку, що відповідає т. H( > Vilni:=x[3], x[5]; sols2:=solve({seq(eq||kk, kk=1..4)},{seq(x[kk], kk=1..6)} minus {Vilni}); map(zz->zz=0,{Vilni}); subs(%, sols2);
В розв’язку, що відповідає т. Q(x 1=5, x 2=-2) від’ємною є базисна змінна Опорна лінія (на рис. 3.1 показана штрих-пунктирною лінією), що проходить через т. В(2, 4), ділить площину Ox 1 x 2 на дві півплощини. Одній з півплощин належить область допустимих значень. В іншій півплощині немає жодної точки допустимих значень, якщо не враховувати т. В(2, 4), яка належить межі півплощин. Саме в цій півплощині розташовані всі точки перетину прямих, які відповідають псевдопланам задачі. Базисні недопустимі розв’язки, що відповідають точкам, які розташовані в тій самій півплощині, що й область допустимих значень, не є псевдопланами, оскільки для цих розв’язків не виконується умова оптимальності. Перевіримо сказане для т. H і Q:
> z:=7*x[1]+6*x[2]: ‘z’[H]=subs(sols1, z); ‘z’[Q]=subs(sols2, z);
Очевидно, що для т. H(x 1 = 5, x 2 = 7), яка належить півплощині з жодною допустимою точкою, умови оптимальності виконуються – цільова функція не може бути покращена збільшенням вільних змінних. Для т. Q(x 1 = 5, x 2 = -2), яка належить тій самій півплощині, що і область допустимих значень, умови оптимальності не виконуються, оскільки цільова функція може бути покращена збільшенням вільної змінної x 5. Після отримання початкового псевдоплану в двоїстому симплекс-методі реалізується послідовний перехід до наступних псевдопланів так, щоб на кожному кроці цільова функція не покращувалася. Перехід від одного псевдоплану до іншого здійснюється за рахунок зміни місцями одної з від’ємних базисних змінних і одної з вільних змінних. Якщо від’ємних базисних змінних декілька, то з них вибирають змінну, абсолютна величина якої найбільша. Якщо таких змінних більше одної, то беруть будь-яку одну з них. З вільних змінних вибирають змінну так, щоб зберегти умови оптимальності. Якщо, принаймні для одної від’ємної базисної змінної, введення її у вільні унеможливлює отримання псевдоплану, то задача розв’язку не має. Алгоритм двоїстого симплекс-методу складається з двох етапів. Етап І. Знаходимо початковий псевдоплан. Етап ІІ. Крок 1. Перевіряємо поточний псевдоплан на допустимість: якщо в поточному псевдоплані відсутні від’ємні змінні, то це і є оптимальний план, тобто задача розв’язана. В протилежному разі переходимо до кроку 2. Крок 2. Переходимо до наступного псевдоплану не покращуючи цільову функцію. Якщо такий перехід здійснити неможливо, то задача розв’язку не має.
Крок 1 та крок 2 етапу ІІ повторюються аж поки не дістанемо розв’язок задачі лінійного програмування або буде виявлено, що задача не має розв’язку. Виконання етапу І, тобто знаходження початкового псевдоплану, можна робити так само, як і знаходження початкового опорного плану в симплекс-методі – методом вибору вільних змінних. На практиці двоїстий метод застосовують саме в тих випадках, коли початковий псевдоплан відомий. Таку ситуацію спостерігатимемо при розв’язанні цілочислових задач лінійного програмування. Розглянемо більш детально здійснення кроку 2. Запишемо загальний розв’язок системи (3.2)
та вираз цільової функції через вільні змінні
де припускається, що Вважатимемо, що
Отже, розв’язок
Теорема 1. Якщо в псевдоплані
Дійсно, в такому випадку із рівняння
випливає, що для будь-яких допустимих значень вільних невідомих, тобто при Теорема 2. Якщо в псевдоплані
Тут слід зауважити, що в надзвичайно популярному посібнику [2] в даній теоремі (теорема 1.14, с. 108) допущено помилку: замість «увеличится» написано «уменьшится». Нехай
та вибрати серед них найменше. Якщо таких найменших чисел виявиться більше ніж одне, то можна вибрати будь-яке з них. Вибір вільної змінної саме за таким правилом забезпечує виконання умов оптимальності в новому базисному розв’язку. Тому вибрати вільну змінну, яка повинна бути переведена в базисні, можна й простим перебором: на кожній ітерації базисна змінна Зауваження. Якщо в задачі (3.1) – (3.3) потрібно знаходити не max а min, то ознакою оптимальності є умови
Приклад 2. Знайти двоїстим симплекс-методом розв’язок задачі (3.4), (3.5), (3.6). Розв’язання. Згідно з етапом І алгоритму двоїстого симплекс-методу шукаємо початковий псевдоплан. Для цього потрібно вибрати вільні змінні та знайти загальний та відповідний базисний розв’язки системи (3.7). Оскільки ми ознайомилися з геометричною інтерпретацією даної задачі, і з’ясували, що псевдоплану відповідає, зокрема, т. H(5, 7), то за вільні візьмемо змінні > z:=7*x[1]+6*x[2]: eq1:=2*x[1]+x[2]+x[3]=8: eq2:=1*x[1]+x[2]+x[4]=6: eq3:=1*x[1]+x[5]=5: eq4:=1*x[2]+x[6]=7: Vilni:=x[5], x[6]: Знаходимо загальний розв’язок системи (3.7) > sols1:=solve({seq(eq||kk, kk=1..4)},{seq(x[kk], kk=1..6)} minus {Vilni}): For i in sols1 do print(i); od:
Значення базисних змінних в базисному розв’язку дорівнюють > map(zz->zz=0,{Vilni}): X1=subs(%, sols1);
Виражаємо цільову функцію через вільні змінні > ‘z’=subs(sols1, z);
Умови оптимальності виконуються, причому серед базисних змінних є від’ємні: > Vilni:=x[3], x[5]: sols2_1:=solve({seq(eq||kk, kk=1..4)},{seq(x[kk], kk=1..6)} minus {Vilni}): ‘z’=subs(sols2_1, z);
Перед змінною Отже, з вільних невідомих потрібно виводити не x 6, а x 5, тобто, вільними будуть x 3, x 6: > Vilni:=x[3], x[6]: sols2_2:=solve({seq(eq||kk, kk=1..4)},{seq(x[kk], kk=1..6)} minus {Vilni}):
Умови оптимальності виконуються. Знайдемо значення базисних змінних > map(zz->zz=0,{Vilni}); X2=subs(%, sols2_2);
Базисна змінна Повернемося до початкового псевдоплану та визначимо вільну змінну, яку потрібно виводити з вільних за допомогою сформульованих правил. В нашому прикладі
Відмінність нашого прикладу від загальних співвідношень полягає тільки в тому, що індекси базисних та вільних змінних розташовані не за порядком. Визначаємо величини Дістанемо вирази для базисних змінних останнього псевдоплану for i in sols2_2 do print(i); od:
Єдина від’ємна змінна серед базисних – > Vilni:=x[3], x[4]: sols3:=solve({seq(eq||kk, kk=1..4)},{seq(x[kk], kk=1..6)} minus {Vilni}): ‘z’=subs(sols3, z);
Збільшенням вільних невідомих покращити цільову функцію неможливо, отже, умови оптимальності виконуються. Знайдемо значення базисних невідомих: > map(zz->zz=0,{Vilni}); X3=subs(%, sols3);
Серед базисних змінних від’ємні значення відсутні, отже, отриманий розв’язок є допустимим, а з урахуванням виконання умов оптимальності маємо оптимальний розв’язок. Цей розв’язок відповідає т. В(x 1 = 2, x 2 = 4) на рис. 3.1. При розв’язанні конкретної задачі лінійного програмування виникає питання вибору методу, що використовується: симплекс-методу або двоїстого симплекс-методу. Двоїстий симплекс-методу зручно використовувати у випадках, коли в ході розв’язання задачі лінійного програмування необхідно додавати нові обмеження. Така ситуація виникає, наприклад, при розв’язанні цілочислових задач лінійного програмування методом Гоморі, що буде розглянуто в підрозділі 4.3. В подібних випадках при застосуванні симплекс-методу після додавання кожного нового обмеження задачу потрібно розв’язувати з самого початку. Застосування в таких випадках двоїстого симплекс-методу зумовлено тим, що відомим є початковий псевдоплан. При розв’язанні звичайних задач лінійного програмування вибір на користь того або іншого методу може бути зроблений в залежності від того, що легше знайти: початковий опорний план чи початковий псевдоплан.
|
||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 342; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.152.251 (0.171 с.) |
 (2.26)
(2.26) (2.27)
(2.27)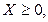 (2.28)
(2.28) (2.29)
(2.29) (2.30)
(2.30) – матриця-рядок змінних прямої задачі;
– матриця-рядок змінних прямої задачі; – матриця-рядок коефіцієнтів цільової функції прямої задачі;
– матриця-рядок коефіцієнтів цільової функції прямої задачі; – матриця коефіцієнтів системи обмежень прямої задачі:
– матриця коефіцієнтів системи обмежень прямої задачі: ;
;  – матриця-рядок вільних членів системи обмежень прямої задачі;
– матриця-рядок вільних членів системи обмежень прямої задачі;  – матриця-рядок змінних двоїстої задачі.
– матриця-рядок змінних двоїстої задачі.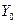 двоїстої до неї задачі можна знайти за допомогою добутку двох матриць
двоїстої до неї задачі можна знайти за допомогою добутку двох матриць , (2.31)
, (2.31) – обернена до матриці
– обернена до матриці  ;
; – матриця, складена із базисних стовпців матриці
– матриця, складена із базисних стовпців матриці  що відповідають оптимальному розв’язку прямої задачі;
що відповідають оптимальному розв’язку прямої задачі; – коефіцієнти цільової функції при базисних невідомих.
– коефіцієнти цільової функції при базисних невідомих. (2.32)
(2.32) (2.33)
(2.33) . (2.34)
. (2.34) (2.35)
(2.35)
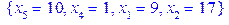
 .
. або
або 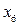 приводить до зменшення цільової функції, отже знайдений опорний план – оптимальний:
приводить до зменшення цільової функції, отже знайдений опорний план – оптимальний: , (2.36)
, (2.36)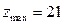 . (2.37)
. (2.37) (2.38)
(2.38) (2.39)
(2.39)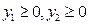 . (2.40)
. (2.40) ,
,  , не накладаються умови невід’ємності, отже, потрібно подати ці змінні у вигляді різниці двох додаткових невід’ємних змінних:
, не накладаються умови невід’ємності, отже, потрібно подати ці змінні у вигляді різниці двох додаткових невід’ємних змінних: . (2.41)
. (2.41)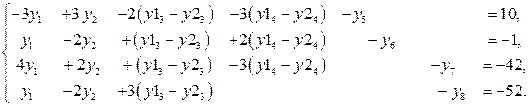
 (2.43)
(2.43)
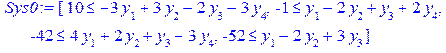

 і подивимося як змінилися рівності, що є елементами списку Sys1
і подивимося як змінилися рівності, що є елементами списку Sys1

 та знаходимо загальний розв’язок
та знаходимо загальний розв’язок


 .
. , що дорівнює zmax (див. (2.37)).
, що дорівнює zmax (див. (2.37)). , (2.44)
, (2.44) . (2.45)
. (2.45) (адже за вільні були прийняті змінні
(адже за вільні були прийняті змінні  та
та  ). Отже, коефіцієнти цільової функції (2.32) при базисних невідомих дорівнюють 10, -1, -52, 0:
). Отже, коефіцієнти цільової функції (2.32) при базисних невідомих дорівнюють 10, -1, -52, 0:
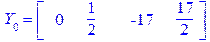 .
.
 (змінна
(змінна 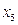 – нас не цікавить, оскільки це додатково введена змінна). Отже, відповідні їм нерівності двоїстої задачі повинні перетворюватися на строгі рівності при оптимальних значеннях змінних двоїстої задачі. Згідно з (2.39), матимемо
– нас не цікавить, оскільки це додатково введена змінна). Отже, відповідні їм нерівності двоїстої задачі повинні перетворюватися на строгі рівності при оптимальних значеннях змінних двоїстої задачі. Згідно з (2.39), матимемо (2.46)
(2.46) . (2.47)
. (2.47) .
. (3.1)
(3.1) , (3.2)
, (3.2) . (3.3)
. (3.3) , (3.4)
, (3.4) (3.5)
(3.5) (3.6)
(3.6) (3.7)
(3.7)





 дістанемо базисний розв’язок, що відповідає точці перетину двох прямих, вздовж одної з яких
дістанемо базисний розв’язок, що відповідає точці перетину двох прямих, вздовж одної з яких  , а вздовж іншої
, а вздовж іншої  . Згідно з даними таблиці 3.1 це буде точка перетину прямих OL та OF, тобто т. О(0, 0). Після знаходження початкового опорного плану вже немає необхідності продовжувати навмання перевибирати вільні змінні, щоб дістати оптимальний план, який відповідає точці В(2, 4). Згідно з ідеями, покладеними в основу симплекс-алгоритму, перехід від неоптимального опорного плану, що відповідає т. О(0, 0), до оптимального опорного плану, що відповідає т. В(2, 4), може бути здійснений одним із цілеспрямованих шляхів – через т. А(4, 0) або через т. С(0, 6).
. Згідно з даними таблиці 3.1 це буде точка перетину прямих OL та OF, тобто т. О(0, 0). Після знаходження початкового опорного плану вже немає необхідності продовжувати навмання перевибирати вільні змінні, щоб дістати оптимальний план, який відповідає точці В(2, 4). Згідно з ідеями, покладеними в основу симплекс-алгоритму, перехід від неоптимального опорного плану, що відповідає т. О(0, 0), до оптимального опорного плану, що відповідає т. В(2, 4), може бути здійснений одним із цілеспрямованих шляхів – через т. А(4, 0) або через т. С(0, 6).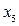 ,
, 



 .
. ) дві базисні змінні
) дві базисні змінні  – від’ємні.
– від’ємні.


 .
. .
.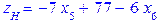 ,
, .
. , (3.8)
, (3.8) , (3.9)
, (3.9) – базисні змінні, а
– базисні змінні, а  – вільні змінні.
– вільні змінні.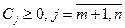 , тобто виконуються умови оптимальності для базисного розв’язку, який може бути отриманий з (3.8) прирівнюванням до нуля всіх вільних змінних:
, тобто виконуються умови оптимальності для базисного розв’язку, який може бути отриманий з (3.8) прирівнюванням до нуля всіх вільних змінних:  .
.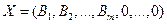 є псевдопланом. Перехід від даного псевдоплану до наступного визначається двома теоремами.
є псевдопланом. Перехід від даного псевдоплану до наступного визначається двома теоремами. є принаймні одне від’ємне число
є принаймні одне від’ємне число  таке, що в (3.8) всі
таке, що в (3.8) всі 
 , то задача (3.1) – (3.3) взагалі не має допустимих розв’язків.
, то задача (3.1) – (3.3) взагалі не має допустимих розв’язків.
 , всі добутки, що стоять під знаком суми в правій частині рівності не більші нуля, отже
, всі добутки, що стоять під знаком суми в правій частині рівності не більші нуля, отже  . Іншими словами, в цьому випадку серед розв’язків даного рівняння немає жодного допустимого розв’язку.
. Іншими словами, в цьому випадку серед розв’язків даного рівняння немає жодного допустимого розв’язку. є від’ємні числа
є від’ємні числа  такі, що для будь-якого з них існують в (3.8) числа
такі, що для будь-якого з них існують в (3.8) числа  , то можна перейти до нового псевдоплану, при якому значення цільової функції задачі (3.1) – (3.3) не збільшиться.
, то можна перейти до нового псевдоплану, при якому значення цільової функції задачі (3.1) – (3.3) не збільшиться. і виконуються умови теореми 2, тобто серед чисел
і виконуються умови теореми 2, тобто серед чисел  є такі, що
є такі, що  . Тоді для того, щоб визначити, яка вільна змінна повинна бути переведена в базисні замість
. Тоді для того, щоб визначити, яка вільна змінна повинна бути переведена в базисні замість  , потрібно для кожного додатного числа
, потрібно для кожного додатного числа  (3.10)
(3.10) і отриманий базисний розв’язок перевіряється на оптимальність. Як тільки буде отримано базисний розв’язок, що задовольняє умови оптимальності, це і означатиме, що здійснений перехід до нового псевдоплану. Якщо заміна
і отриманий базисний розв’язок перевіряється на оптимальність. Як тільки буде отримано базисний розв’язок, що задовольняє умови оптимальності, це і означатиме, що здійснений перехід до нового псевдоплану. Якщо заміна  для будь-якої вільної невідомої
для будь-якої вільної невідомої  не дозволяє отримати псевдоплан, то задача (3.1) – (3.3) розв’язку не має. Очевидно, що простий перебір є абсолютно неефективним через великий обсяг обчислень. Але дозволяє краще зрозуміти сутність ідей, покладених в основу двоїстого симплекс-методу.
не дозволяє отримати псевдоплан, то задача (3.1) – (3.3) розв’язку не має. Очевидно, що простий перебір є абсолютно неефективним через великий обсяг обчислень. Але дозволяє краще зрозуміти сутність ідей, покладених в основу двоїстого симплекс-методу.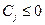 і замість (3.10) потрібно користуватися співвідношенням, що має протилежний знак
і замість (3.10) потрібно користуватися співвідношенням, що має протилежний знак . (3.11)
. (3.11) :
: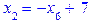 ,
, ,
, ,
, .
. .
. .
. .Отже, маємо початковий псевдоплан. Для переходу до наступного псевдоплану нам потрібно одну з від’ємних змінних поміняти місцями з одною із вільних змінних. Вибираємо серед від’ємних ту, абсолютна величина якої найбільша, тобто
.Отже, маємо початковий псевдоплан. Для переходу до наступного псевдоплану нам потрібно одну з від’ємних змінних поміняти місцями з одною із вільних змінних. Вибираємо серед від’ємних ту, абсолютна величина якої найбільша, тобто  або
або 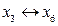 , тобто, вільними будуть
, тобто, вільними будуть  .
.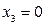 ,
,  на рис. 3.1 відповідає т. Q, яка не належить півплощині, що містить всі точки, які відповідають псевдопланам задачі.
на рис. 3.1 відповідає т. Q, яка не належить півплощині, що містить всі точки, які відповідають псевдопланам задачі. ‘z’=subs(sols2_2, z); (3.12)
‘z’=subs(sols2_2, z); (3.12) ,
, .
. . Отже, маємо псевдоплан, що відповідає т. G(
. Отже, маємо псевдоплан, що відповідає т. G( ). Звернемо увагу на те, що в т. H(5, 7) значення цільової функції дорівнює 77, а в т. G(0,5, 7) дорівнює 45,5. Тобто, в задачі на max перехід від одного псевдоплану до іншого відбувається за умови незбільшення цільової функції (в задачі на min – за умови її незменшення).
). Звернемо увагу на те, що в т. H(5, 7) значення цільової функції дорівнює 77, а в т. G(0,5, 7) дорівнює 45,5. Тобто, в задачі на max перехід від одного псевдоплану до іншого відбувається за умови незбільшення цільової функції (в задачі на min – за умови її незменшення). , а співвідношення (3.8) та (3.9) мають вигляд відповідно
, а співвідношення (3.8) та (3.9) мають вигляд відповідно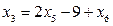 та
та  .
. , для вільної змінної x 6 -
, для вільної змінної x 6 -  . Отже, оскільки
. Отже, оскільки  , то з вільних потрібно виводити змінну x 5. Цей же результат ми дістали і простим перебором. За формальними правилами результат здобувається простіше. Простий перебір був наведений для висвітлення геометричної інтерпретації механізму переходу від одного псевдоплану до іншого.
, то з вільних потрібно виводити змінну x 5. Цей же результат ми дістали і простим перебором. За формальними правилами результат здобувається простіше. Простий перебір був наведений для висвітлення геометричної інтерпретації механізму переходу від одного псевдоплану до іншого.  ,
,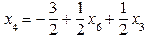 ,
, ,
, .
. , її і будемо виводити із базисних змінних. Для вибору вільної змінної, замість якої вводитимемо
, її і будемо виводити із базисних змінних. Для вибору вільної змінної, замість якої вводитимемо  , j =3, 6 (див. (3.12)): x 3→
, j =3, 6 (див. (3.12)): x 3→  , x 6→
, x 6→  . Оскільки
. Оскільки  , то з вільних потрібно виводити змінну х6. Отже, вибираємо за вільні змінні х3, х4,знаходимо загальний розв’язок та виражаємо цільову функцію через вільні змінні:
, то з вільних потрібно виводити змінну х6. Отже, вибираємо за вільні змінні х3, х4,знаходимо загальний розв’язок та виражаємо цільову функцію через вільні змінні: .
. ,
, .
.


