Графічний метод розв’язання задач цілочислового програмування

Спочатку знайдемо оптимальний план задачі (4.5) – (4.7). Для цього побудуємо область допустимих розв’язків SABC, градієнт grad та опорну лінію MN, перпендикулярну до градієнта (рис. 4.3). Пересуваючи опорну лінію паралельно собі в напрямі градієнта, визначаємо крайню точку В на виході з області допустимих значень SABC.

 

Рисунок 4.3 – Оптимальне значення задачі лінійного програмування (4.5) – (4.7) досягається в точці В(3.4; 2.22), найближча до неї точка т. F(3, 2), але оптимальне значення цілочислової задачі (4.5) – (4.8) досягається в точці G(4; 1)

 

Знаходження оптимального розв’язку цілочислової задачі принципово нічим не відрізняється від наведеного алгоритму. З урахуванням додаткової умови (4.8) область допустимих значень перетворюється до області DEFGH, крайньою точкою на виході з якої є т. G(4, 1). На рис. 4.3 крайнє положення опорної лінії на виході з області DEFGH зображено штриховою лінією, що паралельна лінії MN.

Розглянемо особливості графічного розв’язання задач цілочислового лінійного програмування в середовищі Maple на прикладі наступної задачі.

Приклад 4

Знайти найбільше значення функції

> restart:

z:= 41*x[1] + 33*x[2]:

‘z’=z,`->`*max;

 

за умови, що її аргументи пов’язані співвідношеннями

> linear_constraints:=map(y->subs(x1=x[1], x2=x[2], y),

[133835*x1-4529360*x2<=-561587, -55167*x1-2182400*x2<=-1084571,

-103761*x1-378664*x2<=-515601, -917135*x1-340041*x2<=-2475628,

55775*x1+557469*x2<=2655572, x1>=0, x2>=0]):

for i from 1 to nops(linear_constraints) do op(i,linear_constraints) od;

,

,

,

,

,

,

.

Невідомі можуть приймати тільки цілі значення: – цілі числа.

Розв’язання. Так само, як це ми робили і для нецілочислової задачі, будуємо область допустимих розв’язків – за допомогою команди plots[inequal] (цей графік присвоєно змінній Maple під ім’ям g10), градієнт – за допомогою команди my_arw та опорну лінію MN (g20):

> x1:=-5:x2:=40:

y1:=-1.0:y2:=6:

g10:=plots[inequal]({op(linear_constraints)}, x[1]=x1..x2, x[2]=y1..y2, optionsfeasible=(color=red), optionsopen=(color=blue, thickness=2), optionsclosed=(color=black, thickness=2), optionsexcluded=(color=cyan)):

my_arw:=(x, y, l, w)->if add(type(args[k], numeric), k=1..nargs)=4*true then[[0, 0], [x, y]], [[x-x*l-y*l*w,

-(-y^2+y^2*l-x^2+x^2*l+x*(x-x*l-y*l*w))/y], [x, y]], [[x-x*l+y*l*w,

-(-y^2+y^2*l-x^2+x^2*l+x*(x-x*l+y*l*w))/y], [x, y]] fi:

c1:=3*4.1: c2:=3*3.3: x1_d:=10: y1_d:=2:

g20:=plot([my_arw(c1, c2, 0.15, 0.2), y1_d-(c1/c2)*(x[1]-x1_d)], x[1]=x1..15, x[2]=y1..12, color=[blue$3, black], thickness=[4$3, 2], scaling=CONSTRAINED):

g30:=PLOT(TEXT([35, 3], ’C’, ALIGNLEFT, FONT(TIMES, ITALIC, 14)), TEXT([7, 9],’M’, ALIGNLEFT, FONT(TIMES, ITALIC, 14)), TEXT([14, -1],’N’, ALIGNLEFT, FONT(TIMES, ITALIC, 14))):

plots[display]([g10, g20, g30], scaling=CONSTRAINED,

view=[ 4..37, 0.5..10]);

Координати градієнта помножили на 0.3: c1:=3*4.1:c2:=3*3.3: – для того, щоб вектор помістився на графіку. В рівнянні опорної лінії точку допустимої області взято т. (10;2). Графічна структура g30 містить буквені позначення M, N, C.

Із отриманого графіка видно, що оптимальним планом нецілочислової задачі є координати т. С, точні значення яких в даному випадку нам не потрібні. Для того, щоб визначити оптимальний план цілочислової задачі, потрібно збільшити частину області допустимих значень навколо т. С. Крім того потрібно якимось чином виділити на графіку точки з цілочисловими координатами. Це можна зробити за допомогою сітки, утвореної горизонтальними та вертикальними прямими з цілочисловими координатами. Для побудови такої сітки автором створена допоміжна процедура my_drid(Xn, Ym), яка формує команду побудови горизонтальних та вертикальних прямих, координати яких задані списками Xn, Ym. Для регулювання області відображення графіка користуватимемося опцією view=[25..37, 0..4] команди plots[display].

> x1_d:=35.43:y1_d:=1.24:

my_drid:=(xn::list, yn::list)->plot([yn[‘i’] $ ‘i’ = 1..nops(yn),[xn[‘i’], t, t=yn[1]..yn[nops(yn)]] $ ‘i’ = 1..nops(xn)], xn[1]..xn[nops(xn)], yn[1]..yn[nops(yn)], color=black, linestyle= [3$nops(yn), 4$nops(xn)], scaling=CONSTRAINED):

g40:=plot([[[x1_d, y1_d]], y1_d-(c1/c2)*(x[1]-x1_d)], x[1]=x1..x2, x[2]=y1..y2, color=black, style=[point,line], symbol=circle, symbolsize=25, linestyle=3, thickness=2, scaling=CONSTRAINED):

plots[display]([g10, g20, g40,my_drid([$ 25..37],

[$ 0..4])], view=[25..37,0..4], scaling=CONSTRAINED);

Зменшуємо діапазон виведення графіка (view=[27..33, 0..3]) та зсуваємо у відповідну область опорну лінію (x1_d:=31:y1_d:=1.5:)

> x1_d:=31:y1_d:=1.5:

g60:=plot([y1_d-(c1/c2)*(x[1]-x1_d)], x[1]=x1..x2, x[2]=y1..y2, color=black, style=[line], symbol=circle,

symbolsize=25, linestyle=3, thickness=2, scaling=CONSTRAINED):

plots[display]([g10, g20, g60, my_drid([$ 25..37], [$ 0..4])],

view=[27..33, 0..3], scaling=CONSTRAINED);

Із отриманого графіка видно, що області допустимих значень не належать точки з цілочисловими координатами, абсциси яких дорівнюють 32 і більше, а ординати 3 і більше. Добре видно, що області допустимих значень належить т. (28; 1). Отже, знову зменшуємо діапазон виведення графіка (view=[28..31, 0.7..2.2])

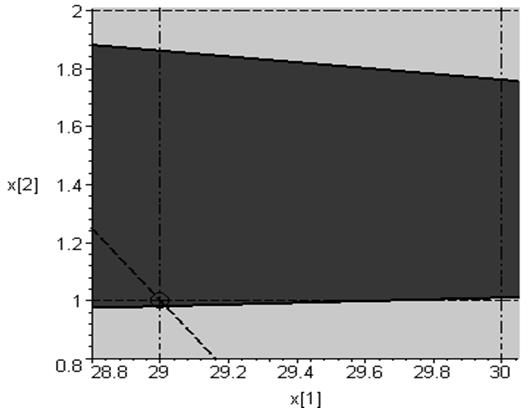
Із графіка видно, що оптимальним планом є координати т. (30; 1), якщо ця точка належить області допустимих значень, або координати т. (29; 1) – в протилежному випадку. Перевіримо належність т. (30; 1) до області допустимих значень:

> plots[display]([g10, g20, g60, my_drid([$ 25..37],

[$ 0..4])], view=[29.9..30.9, 0.97..1.1], scaling=CONSTRAINED);

Очевидно, що т. (30, 1) знаходиться поза областю допустимих значень. Отже,

> x1_d:=29:y1_d:=1:

g50:=plot([[[x1_d, y1_d]], y1_d-(c1/c2)*(x[1]-x1_d)], x[1]=x1..x2, x[2]=y1..y2, color=black, style=[point, line], symbol=circle, symbolsize=25, linestyle=3, thickness=2, scaling=CONSTRAINED):

plots[display] ([g10, g20, g50, my_drid([$25..37], [$0..4])], view=[28.8..30.05, 0.8..2.01], scaling=CONSTRAINED);

 

Оптимальний план , оптимальне значення цільової функції

>‘z[max]’=subs(x[1]=29, x[2]=1, z);

 

.

Для того, щоб наведені в цьому прикладі програми були доступні в DEMO-Maple, потрібно тільки вилучити опцію symbolsize=25 команди plot.

Ми розглянули варіанти, що піддаються геометричній інтерпретації. Із збільшенням розмірності процес розв’язання цілочислової задачі ускладнюється.