
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Огляд засобів пакета лінійної оптимізації simplexСодержание книги
Поиск на нашем сайте Команда, яка надає доступ до всіх команд пакета, має вигляд with(simplex); Після виконання указаної команди в оперативну пам’ять комп’ютера завантажуються усі процедури пакета. Для здійснення доступу тільки до однієї або декількох команд пакета можна скористатися тією самою командою з додатковими опціями with(simplex, nam1, nam2,…); де nam1,… – назви команд пакета: basis, convexhull, cterm, define_zero, display, dual, feasible, maximize, minimize, pivot, pivoteqn, pivotvar, ratio, setup, standardize, що викликають відповідні процедури, які надають можливість користувачеві поетапно розв’язувати задачу лінійного програмування за симплекс-методом [67]. Розглянемо найбільш важливі для розв’язування задачі лінійного програмування функції maximize і minimize. Синтаксис звернення до указаних команд має доволі простий вигляд maximize (f, consts), minimize (f, consts), де f – лінійний вираз, який описує цільову функцію задачі; consts – множина або список лінійних обмежень задачі. Процедури maximize та minimize повертають або множину рівностей, які описують оптимальний план > with(simplex): maximize(-x[1]+2*x[2]+3*x[3], {x[1]+2*x[2]-3*x[3]<=4, 5*x[1]-6*x[2]+7*x[3]<=8, 9*x[1]+10*x[3]<=11}, NONNEGATIVE);
> minimize(-x[1]+2*x[2]+3*x[3], {x[1]+2*x[2]-3*x[3]<=4, 5*x[1]-6*x[2]+7*x[3]<=8, 9*x[1]+10*x[3]<=11}, NONNEGATIVE);
або порожню множину (рис. 5.1), якщо система обмежень consts є несумісною > maximize(3*y[1]-y[2], {-y[1]-y[2]>=-1, y[1]+y[2]>=2}, NONNEGATIVE);
Рисунок 5.1 – Оптимальний план або порожня множина, або NULL, якщо цільова функція на допустимій множині необмежена
> maximize(47*y[1]+43*y[2], {-3*y[1]-y[2]<=-9, 17*y[1]-64*y[2]<=51, 6*y[1]+18*y[2]>=56}, NONNEGATIVE);
Звернемо увагу, що у випадку відсутності розв’язку задачі ЛП через необмеженість області допустимих значень (рис. 5.2) команда maximize повертає результат NULL, який не супроводжується жодним записом в області виведення результатів виконання команди на екрані монітора. Очевидно, якщо переформулювати указану задачу на знаходження найменшого значення, то розв’язок буде знайдено
> minimize(47*y[1]+43*y[2], {-3*y[1]-y[2]<=-9, 17*y[1]-64*y[2]<=51, 6*y[1]+18*y[2]>=56}, NONNEGATIVE);
Рисунок 5.2 – Область допустимих значень
Оптимальний розв’язок може бути підставлений у цільову функцію для одержання її екстремального значення. Це можна зробити за допомогою команд eval або subs > 'z'[min] = subs ({y[1]=53/24, y[2]=19/8}, 47*y[1]+43*y[2]);
Інші функції пакета simplex Функція display(C) виводить множина лінійних залежностей С в матричній формі: > display([x[1]+3*x[2]<=12, -2*x[1]-x[2]<=-6, 19*x[1]-8*x[2]<=57]);
Ця функція може бути використана для наглядного переходу до двоїстої задачі. Функція dual(f,C,y) повертає двоїсту задачу до заданої, де f – цільова функція; С – множина лінійних залежностей системи обмежень; y – позначення змінної двоїстої задачі > dual((-4)*x[1]-2*x[2], [x[1]+3*x[2]<=12, -2*x[1]-x[2]<=-6, 19*x[1]-8*x[2]<=57], y);
Для отримання більш наглядної форми запису отриманої задачі можна використати уже знайому нам команду display > display(%[2]);
Функція f easible перевіряє систему на сумісність(якщо одержано true, то система обмежень сумісна, якщо false – несумісна); > feasible({2*x+3*y<=4, 5*x+6*y=9}, NONNEGATIVE);
> feasible({-y[1]-y[2]>=-1, y[1]+y[2]>=2}, NONNEGATIVE);
Останній приклад відповідає пустій множині допустимих значень невідомих, що зображена на рис. 5.1.
|
||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 ,
, ,
,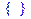

 .
.
 .
.
 .
.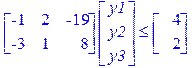 .
.




