Разыгрывание дискретной случайной величины

Пусть требуется разыграть дискретную случайную величину Х, т.е. получить последовательность ее возможных значений хi(i=1,2,3…,n), зная закон распределения Х:

Х x1 x2 … xn

p p1 p2 … pn

Обозначим через R непрерывную случайную величину, распределённую равномерно в интервале (0,1), а через rj (j=1,2,3,…,n)- ее возможные значения, т.е. случайные числа.

Разобьём интервал 0≤R<1 на оси Оr точками с координатами p1,p1+p2, p1+p2+p3,…,p1+p2+p3+…+pn-1 на n частичных интервалов Δ1,Δ2,Δ3,…,Δn

Дл. Δ1= p1-0= p1

Дл. Δ2= p1+p2- p1= p2

……………………

Дл. Δn=1-(p1+p2+p3+…+pn-1)= pn

Видим, что длина частичного интервала с индексом i равна вероятности с тем же индексом:

Дл. Δi=pi (*)

Теорема. Если каждому случайному числу rj (0≤ rj<1), которое попало в интервал Δi, ставить в соответствии возможное значение хi, то разыгрываемая величина будет иметь заданный закон распределения:

Х x1 x2 … xn

p p1 p2 … pn

Доказательство. Так как при попадании случайного числа rj в частичный интервал Δi разыгрываемая величина принимает возможное значение хi, а таких интервалов всего n, то разыгрываемая величина имеет те же возможные значения, что и Х, а именно х1,х2,х3,…,хn.

Вероятность попадания случайной величины R в интервал Δi равно его длине, а всилу (*) Дл. Δi=pi. Т.о., вероятность попадания R в интервал Δi равно pi. Следовательно, вероятность того, что разыгрываемая величина примет возможное значение хi, также равна pi (поскольку мы условились в случае попадания случайного числа rj в частичный интервал Δi считать, что разыгрываемая величина приняла возможное значение хi).

Итак, разыгрываемая величина имеет заданный закон распределения.

Правило. Для того чтобы разыграть дискретную случайную величину, заданную законом распределения.

Х х1 х2 … хn

p p1 p2 … pn

Надо:1) разбить интервал (0,1) на оси Оr на n частичных интервалов: Δ1-(0;p1), Δ2-(p1;p1+p2),…, Δn –(p1+p2+p3+…+pn-1;1)

2) выбрать случайное число rj

Если rj попало в частичный интервал Δi, то разыгрываемая дискретная случайная величина приняла возможное значение хi

 

21.Системы массового обслуживания,основные понятия,граф состояния.

Системы МО являются частью более широкого класса динамических систем, которые иногда называют системами потоков. Системой потоков называется система, в которой некоторые предметы перемещаются по одному или нескольким каналам с ограниченной пропускной способностью с целью перемещения из одной точки в другую.
При анализе систем потоков их разбивают на два основных класса:
Ø регулярные системы, т. е. системы, в которых потоки ведут себя предсказуемым образом (известны величина потока и время его появления в канале). В случае, когда канал один, расчет системы тривиален. Очевидно, что между интенсивностью потока R и скоростью обслуживания с есть соотношение R < c;
Ø нерегулярные системы, т. е. системы, в которых потоки ведут себя непредсказуемым образом.
Более интересным является случай регулярного потока, который распределяется по сети каналов. Очевидно, что условие R < c сохраняется для каждого канала. При этом возникает сложная комбинаторная задача.

Рис. 7.20

Имеется семь дорог. Необходимо перевезти груз из А в Д. Пропускная способность каждого канала известна. Какова пропускная способность сети и каким путем должен следовать поток? Решить эту задачу можно с помощью теоремы о максимальном потоке, которую мы рассматривали ранее (рис. 7.20).
Ко второму классу относятся случайные вероятные потоки, в которых время поступления требования не определено, число требований непредсказуемо. Решением таких задач и занимается теория массового обслуживания.
В общем случае система массового обслуживания может быть представлена на рис. 7.21.

Рис. 7.21

Предметом теории массового обслуживания является установление зависимости между характером потока заявок, числом каналов, производительностью, правильностью работы и эффективностью.
В качестве характеристик эффективности могут применяться следующие величины и функции:

· среднее количество заявок, которые может обслужить СМО в единицу времени;

· среднее количество заявок, получающих отказ и покидающих СМО;

· вероятность того, что поступившая заявка немедленно будет обслужена;

· среднее время ожидания в очереди;

· среднее количество заявок в очереди;

· средний доход СМО в единицу времени и другие экономические показатели СМО.

Анализ СМО упрощается, если в системе протекает марковский процесс, тогда систему можно описать обыкновенными дифференциальными уравнениями, а предельные вероятности – линейными алгебраическими уравнениями.
Марковский процесс требует, чтобы все потоки были пуассоновскими (без последействий), но аппарат марковских процессов используется и тогда, когда процесс отличен от марковского. В этом случае характеристики СМО могут быть оценены приблизительно: чем сложнее СМО, тем точнее приближение.

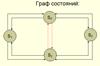
Определение: Граф состояний – графическая схема случайного процесса с дискретными состояниями;

Пример: Устройство S состоит из двух узлов.

Состояния:

S₀ – оба узла исправны:

S₁ – первый узел ремонтируется, второй исправен;

S₂ - второй узел ремонтируется, первый исправен;

S₃ - оба узла ремонтируются;

 

Уравнение Колмогорова