
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Различные классификации математических моделей.Стр 1 из 10Следующая ⇒
Этапы компьютерного моделирования. Примеры.
1. Объект изучения 2. Формальная модель 3. Программирование модели 4. Отладка тестирования 5. Компьютерный эксперимент 6. Информационная модель Моделирование начинается с объекта изучения. На первом этапе формируются законы управляющие исследованием. Отбираются существенные параметры объекта исследования. Отбрасываются несущественные. Потеря может повлиять на результат. На этом этапе идёт подготовка к обработке на компьютере. Строится формальная модель. Переход от описательной модели к конкретному математическому наполнению. Указывается перечень параметров, которые влияют на поведение объекта – исходные данные, и которые желательно получить – результат. Формализуются зависимости между выделенными параметрами, накладываются ограничения на их допустимые значения. Результатом формализации является математическая модель. На втором этапе формальная модель реализуется на компьютере. Подбираются программные средства (графические среды, текстовые редакторы, среды программирования, электронные таблицы и пр.); От выбора программной среды зависит алгоритм построения компьютерной модели и форма его представления. Написанная программа отлаживается и тестируется на специально подготовленных тестовых моделях. Проверить компьютерную модель на соответствие оригиналам часто удаётся, с помощью простых модельных примеров, когда результат заранее известен. На третьем этапе мы выполняем вычислительный эксперимент, т.е. исследуем поведение модели в тех или иных случаях при различных наборах динамических параметров. Производится попытка прогноза и оптимизации чего-либо в зависимости поставленных задач. На четвёртом этапе проводится отладка тестирования. На пятый этап можно переходить только после того, как тестирование модели прошло успешно, и вы уверены, что создана именно та модель, которую необходимо исследовать. Результатом будет являться информационная модель в виде графиков, диаграмм, таблиц.
Цель моделирования 1) познание окружающего мира Зачем человек создает модели? Чтобы ответить на этот вопрос, надо заглянуть в далекое прошлое. Несколько миллионов лет назад, на заре человечества, первобытные люди изучали окружающую природу, чтобы научиться противостоять природным стихиям, пользоваться природными благами, просто выживать.
Накопленные знания передавались из поколения в поколение устно, позже письменно и наконец с помощью предметных моделей. Так родилась, к примеру, модель Земного шара — глобус — позволяющая получить наглядное представление о форме нашей планеты, ее вращении вокруг собственной оси и расположении материков. Такие модели позволяют понять, как устроен конкретный объект, узнать его основные свойства, установить законы его развития и взаимодействия с окружающим миром моделей.
2) создание объектов с заданными свойствами (определяется постановкой задачи «как сделать, чтобы...». 3) определение последствий воздействия на объект и принятие правильного решения. Цель моделирования задач типа «что будет, если...». (что будет, если увеличить плату за проезд в транспорте, или что произойдет, если закопать ядерные отходы в такой-то местности?) 4) эффективность управления объектом (или процессом). Поскольку критерии управления бывают весьма противоречивыми, то эффективным оно окажется только при условии, если будут «и волки сыты и овцы целы».
Дифференциальные модели. Методы. Задачи. Модель математического маятника. Решения уравнения движения. Гармонические колебания Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы: Нелинейный маятник Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
Параметр
Модель «конкурирующие виды» Рассмотрим 2 вида животных, растений или бактерий, которые конкурируют друг с др. за продовольствие, доступное в их общей среде. Обозначим за х(t), у(t) численности их популяций в момент времени t. Предположим, что в отсутствии любых других видов данный вид имел бы ограниченную численность популяции, в отсутствие любого взаимодействия или конкурирующего вида численности их популяций удовлетворяли бы дифференциальному уравнению:
Предположим, что конкуренция влияет на скорость снижения числ.-ти любой популяции, которая пропорциональна произведению их численности х*у. Добавим слагаемые с отрицательными коэффициентами пропорциональности -
В этой системе
(0;0) (0;
(8) имеет единственную интерпретацию. Из (5) видно, что коэффициенты Общий анализ системы (6) показывает следующее: 1. Если 2. Если
Уравнение Колмогорова
Метод обратных функций. Пусть требуется разыuрать НСВХ, зная функцию распределения F(x). Воспользуемся теоремой: Если ri- случайное число, то возможное значение хi разыгрываемой НСВХ с заданной функцией распределения F(x), соответствующее ri, является корнем уравнения F(xi) =ri. На основании данной теоремы сформулируем правило разырывания значений НСВХ, знаяя ее функцию распределения F(x): Необходимо выбрать случайное число ri, приравнять его функции распределения и решить относительно хi уравнение: F(xi) =ri. Пример: НСВХ распределена по показательному закону. требуется найти явную формулу для разыгрывания возможных значений Х. Известно, что функция распределения при показательном законе имеет вид
Составим и решим относительно х уравнение:
откуда:
Выбирая случайные числа ri, подставляя их в полученную явную формулу, разыграем возможные значения НСВХ. Если известна плотность распределения НСВХ, то для разыгрывания значений НСВХ, решают уравнение:
Пример: Задана плотность вероятности НСВХ: вне этого интервала – 0. Найти явную формулу для разыгрывания значений НСВХ. Составим и решим относительно хi уравнение:
6 .2. Метод суперпозиции. Пусть функция распределения разыгрываемой НСВХ задана линейной комбинацией двух функций распределения: F(x)= C1 F1(x) +C2 F2(x), где C1>0, C2>0. При х¥® каждая из функций распределения стремится к единице,, поэтому C1 + C2 =1. Введем вспомогательную ДСВZ с законом распределения:
Выберем два независимых случайных числа r1 и r2. По числу r1 разыграем возможное значение Z. Если z=1, то возможное значение х найдем из уравнения F1(x) = r2, а если z =2, то из уравнения F2(x) = r2. Пример: Найти явные формулы для разыгрывания НСВХ, заданной функцией распределения: F(x) = 1- 0,25(e-2x + 3e-x). Используя метод суперпозиций, представим функцию в виде F(x) =0,25(1 – e-2x) +0,75 (1 – e-x). Откуда С1 =0,25; С2 =0,75; F1(x) = 1 – e-2x, F2(x) = 1 – e-x. Введем ДСВZ:
Интервал (0;1) разобьем на частичные интервалы (0; 0,25) и (0,25; 1). Выберем случайные числа r1 и r2. Если r1 принадлежит интервалу (0; 0,25), то решаем уравнение: 1 – e-2x= r2, если r1 принадлежит интервалу (0,25; 1), то – уравнение: 1 – e-x = r2. Таким образом, получаем возможные значения НСВХ.
Цепи Маркова. Цепи Маркова названы так в честь выдающегося русского математика, Андрея Андреевича Маркова, который много занимался случайными процессами и внес большой вклад в развитие этой области. В последнее время можно услышать о применении цепей Маркова в самых разных областях: в современных веб-технологиях, при анализе литературных текстов или даже при разработке тактики игры футбольной команды. У тех, кто не знает что такое цепи Маркова, может возникнуть ощущение, что это что-то очень сложное и почти недоступное для понимания.
Нас, конечно, больше всего интересует какое отношение имеют цепи Маркова к лотереям и можно ли их использовать для прогноза номеров. По-видимому, использовать цепи Маркова для моделирования последовательности различных тиражей нет смысла. То, что происходило с шариками в тираже, никак не повлияет на результаты следующего тиража, поскольку после тиража шары собирают, а в следующем тираже их укладывают в лоток лототрона в фиксированном порядке. Связь с прошедшим тиражом при этом теряется. Совсем необязательно, что между разливными тиражами совсем нет никакой корреляции. Возможно, она есть, но тогда она носит характер общий для всех тиражей. Это можно анализировать, но другими методам - цепь Маркова здесь в качестве модели не годится. Другое дело последовательность выпадения шаров в пределах одного тиража. В этом случае выпадение очередного шара определяется состоянием лототрона на момент выпадения предыдущего шара. Таким образом, последовательность выпадений шаров в одном тираже является цепью Маркова, и мы можем использовать такую модель. В общем случае для анализа Марковской цепи строится матрица вероятностей переходов. Это таблица вероятностей переходов между двумя любыми возможными состояниями системы. Т.е., если система может находится в N различных состояниях S1, S2, S3, … SN, то можно определить вероятность перехода p12 из состояния S1 в состояние S2, вероятность перехода p13 из состояния S1 в состояние S3, вероятность перехода p23 из состояния S2 в состояние S3 и так далее. Все вместе эти вероятности образуют таблицу (матрицу) размером N x N.
При анализе числовых лотерей здесь имеется большая трудность. Состояние лототрона после выпадения очередного шара определяет дальнейшие события, но проблема в том, что это состояние нам неизвестно. Все что нам известно, что выпал некоторый шар. Но при выпадении этого шара, остальные шары могут быть расположены различным образом, так что имеется группа из очень большого числа состояний соответствующая одному и тому же наблюдаемому событию. Поэтому мы можем построить лишь матрицу вероятностей переходов между такими группами состояний. Эти вероятности являются усреднением вероятностей переходов между различными отдельными состояниями, что конечно, снижает эффективность применения модели Марковской цепи к числовым лотереям. Тем не менее, в каждой группе основной вклад будут вносить те состояния, для которых значения вероятностей перехода наибольшие, и в целом модель должна быть вполне работоспособной. Для увеличения точности, в принципе, можно учитывать, не одно, а два (или даже больше) предшествующих выпадения шаров. При этом мы заменяем недостаток знаний о текущем состоянии информацией о связи его с предыдущими состояниями. Эта модель соответствует последовательности случайных событий, в которой вероятность каждого события зависит только от двух предыдущих событий. Такие последовательности называют цепями Маркова 2-го порядка (и аналогично можно определить цепи Маркова более высоких порядков). Модель тиража основанная на цепи Маркова 2-го порядка может обеспечить большую точность, хотя расчеты для такой цепи становятся намного сложнее. Но главная проблема с цепью 2-го порядка даже не в сложности расчета, а в количестве требуемых исходных данных. Чтобы построить статистически значимую переходную матрицу цепи 1-го порядка для лотереи "20 из 80" достаточно несколько сотен тиражей. А построение матрицы цепи 2-го порядка для той же лотереи потребует больше 10 тысяч тиражей. В мире немного найдется лотерей, для которых имеется такая статистика, и даже для них ее вряд ли стоит использовать, так как она накапливается за длительный период и за это время не раз меняются комплекты шаров и лототроны. Поэтому разумнее ограничится цепями 1-го порядка и брать для построения матрицы только тиражи за последний год или два. 19. Приближенное разыгрывание нормальной случайной величины. Напомним предварительно, что если случайная величина R равномерно распределена в интервале (0; 1), то ее математическое ожидание и дисперсия соответственно равны: M(R)=1/2,(*) D®=1/12.(**) Составим сумму nнезависимых, распределённых равномерно в интервале (0; 1) случайных величин Rj (j=1, 2,…,n):
Для нормирования этой суммы найдём предварительно ее математическое ожидание и дисперсию. Известно, что математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых. Сумма (***) содержит n слагаемых, математическое ожидание каждого из которых в силу (*) равно 1/2; следовательно, математическое ожидание суммы (***) М( D( Отсюда среднее квадратичное отклонение суммы (***)
Пронормируем рассматриваемую сумму, для чего вычислим математическое ожидание и разделим результат на среднее квадратичное отклонение:
В силу центральной предельной теоремы при n-›∞ распределение этой нормированной случайной величины стремится к нормальному с параметрами а=0 и
Правило. Для тог чтобы разыграть возможные значения хi нормальной случайной величины Х с параметрами а=0 и
РАЗЛИЧНЫЕ КЛАССИФИКАЦИИ МАТЕМАТИЧЕСКИХ МОДЕЛЕЙ. К классификации математических моделей можно подходить с разных позиций, положив в основу классификации различные принципы.Можно классифицировать модели по отраслям наук (математические модели в физике, биологии, социологии и т.д.) и по применяемому математическому аппарату (модели, основанные на использовании обыкновенных дифференциальных уравнений, дифференциальных уравнений в частных производных, стохастических методов, дискретных алгебраических преобразований и т.д.). Если поставить на первое место цели моделирования, то можно прийти к следующей классификации:• дескриптивные (описательные) модели;• оптимизационные модели;• многокритериальные модели;• игровые модели;• имитационные модели. Остановимся на этой классификации подробнее и поясним ее на примерах. Моделируя движение кометы, вторгшейся в Солнечную систему, мы описываем ситуацию (предсказываем траекторию полета кометы, расстояние, на котором она пройдет от Земли и т.д.), т.е. ставим чисто описательные цели. У нас нет никаких возможностей повлиять на движение кометы, что-то изменить в процессе моделирования. В оптимизационных моделях мы можем воздействовать на процессы, пытаясь добиться какой-то цели. В этом случае в модель входит один или несколько параметров, доступных нашему влиянию. Например, меняя тепловой режим в зернохранилище, мы можем стремиться подобрать такой, чтобы достичь максимальной сохранности зерна, т. е. оптимизируем процесс. Часто приходится оптимизировать процесс по нескольким параметрам сразу, причем цели могут быть весьма противоречивыми. Ясно, что эти цели, вообще говоря, совсем не совпадают, т.е. при моделировании будет несколько критериев, между которыми надо искать баланс. В этом случае говорят о многокритериальных моделях. Игровые модели могут иметь отношение не только к детским играм (в том числе и компьютерным), но и к вещам весьма серьезным. В современной математике есть специальный раздел – теория игр, изучающий методы принятия решений в условиях неполной информации. Наконец, бывает, что модель в большой мере подражает реальному процессу, т.е. имитирует его. Например, моделируя динамику численности микроорганизмов в колонии, можно рассматривать совокупность отдельных объектов и следить за судьбой каждого из них, ставя определенные условия для его выживания, размножения и т.д. При этом иногда явное математическое описание процесса не используется, заменяясь некоторыми словесными условиями (например, по истечении некоторого отрезка времени микроорганизм делится на две части, а другого отрезка – погибает). Можно сказать, что чаще всего имитационное моделирование применяется в попытке описать свойства большой системы при условии, что поведение составляющих ее объектов очень просто и четко сформулировано. Математическое описание тогда производится на уровне статистической обработки результатов моделирования при нахождении макроскопических характеристик системы. Такой компьютерный эксперимент фактически претендует на воспроизведение натурного эксперимента. Еще один подход к классификации математических моделей подразделяет их на детерминированные и стохастические (вероятностные). В детерминированных моделях входные параметры поддаются измерению однозначно и с любой степенью точности, т.е. являются детерминированными величинами. Соответственно, процесс эволюции такой системы детерминирован. В стохастических моделях значения входных параметров известны лишь с определенной степенью вероятности, т.е. эти параметры являются стохастическими; соответственно, случайным будет и процесс эволюции системы. При этом, выходные параметры стохастической модели могут быть как величинами вероятностными, так и однозначно определяемыми. Наконец, если ограничиться непрерывными детерминистскими моделями, то их часто подразделяют на системы с сосредоточенными параметрами и системы с распределенными параметрами. Системы с сосредоточенными параметрами описываются с помощью конечного числа обыкновенных дифференциальных уравнений для зависящих от времени переменных.Пространство состояний имеет здесь конечную размерность.В противоположность этому под системами с распределенными параметрами понимают системы, описываемые конечным числом дифференциальных уравнений в частных производных.Здесь переменные состояния в каждый момент времени есть функции одной или нескольких пространственных переменных.Пространство состояний имеет в этом случае бесконечную размерность, т.е. система обладает бесконечным числом степеней свободы.
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-02-07; просмотров: 187; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.27.232 (0.069 с.) |
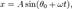 где A — амплитуда колебаний маятника, θ0 — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями.
где A — амплитуда колебаний маятника, θ0 — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями. где — это синус Якоби. Для
где — это синус Якоби. Для  он является периодической функцией, при малых совпадает с обычным тригонометрическим синусом.
он является периодической функцией, при малых совпадает с обычным тригонометрическим синусом. определяется выражением
определяется выражением  где
где  — энергия маятника в единицахt-2Период колебаний нелинейного маятника
— энергия маятника в единицахt-2Период колебаний нелинейного маятника где K — эллиптический интеграл первого рода.
где K — эллиптический интеграл первого рода.
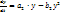 (5)
(5)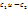 . В уравнениях (5) получим систему, описывающую конкуренцию:
. В уравнениях (5) получим систему, описывающую конкуренцию: 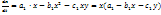
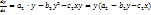 (6)
(6)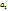 ,
, 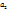 ,
,  ,
,  ,
,  ,
, 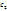 положительные.
положительные.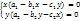

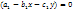



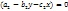

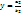
 (7)
(7) 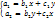
 ) (
) (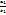 ;0) Предположим, что уравнение имеет единственное решение, и составим точки равновесия в первом квадранте. Надо найти точку (
;0) Предположим, что уравнение имеет единственное решение, и составим точки равновесия в первом квадранте. Надо найти точку ( ), эта точка представляет возможность сосуществования двух видов с постоянными не равными 0, равновесными численными популяций
), эта точка представляет возможность сосуществования двух видов с постоянными не равными 0, равновесными численными популяций 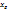 и
и  . Устойчивость этой точки зависит от того, какое из равенств выполняется:
. Устойчивость этой точки зависит от того, какое из равенств выполняется: (8)
(8) представляют эффект конкуренции м/у этими двумя популяциями, следовательно, произведение
представляют эффект конкуренции м/у этими двумя популяциями, следовательно, произведение 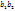 - это мера подавления, а
- это мера подавления, а 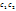 - мера конкуренции.
- мера конкуренции. так, что конкуренция незначительна по сравнению с подавлением, то точка
так, что конкуренция незначительна по сравнению с подавлением, то точка  ) – устранимая точка равновесия, которая приближает каждое решение при t
) – устранимая точка равновесия, которая приближает каждое решение при t  , т.о. оба вида могут сосуществовать.
, т.о. оба вида могут сосуществовать. так, что конкуренция доминирует, то точка
так, что конкуренция доминирует, то точка  , либо у(t)
, либо у(t) 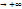 , т.е. 2 вида не могут сосуществовать
, т.е. 2 вида не могут сосуществовать




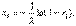


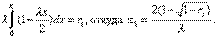
 (***)
(***)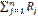 )= n/12
)= n/12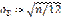 .
. /
/ . При конечном n распределение приближённо нормальное. В частности, при n=12 получим достаточно хорошее и удобное для расчета приближение
. При конечном n распределение приближённо нормальное. В частности, при n=12 получим достаточно хорошее и удобное для расчета приближение .
. , надо сложить 12 независимых случайных чисел и из полученной суммы вычесть 6:
, надо сложить 12 независимых случайных чисел и из полученной суммы вычесть 6: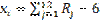 .
.


