
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечные ожидания и тупики.Содержание книги
Поиск на нашем сайте
Проблема бесконечного ожидания может возникнуть в любой обстановке, предусматривающей параллельное исполнение процессов. Пусть транзакция Простой способ избежать этого: регистрировать все запросы и удовлетворять их в порядке очерёдности. Вторая, более серьёзная проблема – тупики. Пример:
… – возможно бесконечное ожидание.
LOCK B LOCK A UNLOCK A UNLOCK B UNLOCK B UNLOCK A Транзакция Ситуация, в которой каждая транзакция из множества S, содержащего не менее 2-х транзакций, ожидает, когда ей будет предоставлена возможность заблокировать элемент, заблокированный в данный момент времени какой-нибудь иной транзакцией из данного множества S, называется тупиком. Подход к решению этой проблемы: 1) Потребовать, чтобы каждая транзакция единовременно запрашивала все нужные ей блокировки. Система либо полностью удовлетворяет такой запрос, либо не предоставляет вообще никаких блокировок и заставляет данную транзакцию ждать, если один или более требуемых элементов заблокирован до транзакции. Это устраняет тупик из примера. 2) Вводится произвольное линейное упорядочивание элементов и все транзакции должны запрашивать блокировки в этом порядке. Это гарантирует установление очередности между транзакциями. Для транзакции, заблокировавшей некоторый элемент, гарантируется возможность заблокировать и все следующие за ним элементы.
3) Совсем иной способ борьбы с тупиками – ничего не предпринимать для их предотвращения, а периодически проверять запросы на блокировки и выявлять: не возникла ли тупиковая ситуация. Облегчает проведение такой проверки алгоритм построения графа, вершины которого обозначают транзакции, а ориентированная дуга
В случае обнаружения тупика нужно произвести снятие всех блокировок (рестарт) хотя бы для одной из попавших в него транзакций (удалить дугу) или сделать откат транзакции (удалить вершину). Протоколы и расписание. Каждая транзакция состоит из элементарных шагов (блокировка, чтение записи и т.д.). Расписанием совокупности транзакций называется порядок, в котором выполняются элементарные шаги этих транзакций. Шаги любой транзакции должны появляться в расписании в порядке их вхождения в программу, прогоном которой является эта транзакция. Расписание считается последовательным, если все шаги каждой транзакции выполняются последовательно; сериализуемым, если результат его реализации всегда эквивалентен результату некоторого последовательного расписания. Для предотвращения несериализуемости расписания вводят протоколы, которые в наиболее общем смысле представляют собой ограничения на последовательность шагов, которые может выполнить транзакция. Например, протоколом является исключающая тупики стратегия запрашивания блокировок элементов в некотором фиксированном порядке.
Простая модель транзакции. Изучим простейшую модель транзакции, которая позволяет говорить о сериализуемости. В этой модели транзакция рассматривается как последовательность операторов блокирования и разблокирования. Каждый блокированный элемент впоследствии должен быть разблокирован. Будем считать, что при между шагом LOCK A и UNLOCK A транзакция осуществляет изменение значения Поставим каждой паре шагов LOCK и UNLOCK однозначную функцию f. Вообще говоря, любой элемент
Пример:
|
||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 329; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.101.250 (0.007 с.) |

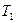 проводит работу с элементом
проводит работу с элементом  , и доступ к элементу
, и доступ к элементу 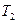 находится в состоянии ожидания; транзакция
находится в состоянии ожидания; транзакция  также запрашивает блокировку
также запрашивает блокировку  , чьё требование удовлетворяется после разблокирования
, чьё требование удовлетворяется после разблокирования  . Затем
. Затем  , что транзакция
, что транзакция  ожидает выполнения своего запроса на блокирование элемента, заблокированного в данный момент транзакцией
ожидает выполнения своего запроса на блокирование элемента, заблокированного в данный момент транзакцией  . Возникновение тупика определяет наличие в построенном указанным способом графе цикла. Если цикла нет, то не существует и тупиков.
. Возникновение тупика определяет наличие в построенном указанным способом графе цикла. Если цикла нет, то не существует и тупиков.

 , где
, где  – начальное значение
– начальное значение 









