
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реляционное исчисление с переменными на доменах.Содержание книги
Поиск на нашем сайте
Различие состоит в следующем: 1. В исчислении с переменными на доменах не существует переменных-кортежей; вместо них существуют переменные на доменах, которые представляют компоненты кортежей. 2. Атом имеет вид: а) б) 3. Формулы в РИ с переменными на доменах используют связки Свободные и связанные переменные определяются так же, как и в РИ с переменными кортежами. Выражение РИ с переменными на доменах имеет вид: где Пример:
- отношение R1 состоит из компонент x1 и x2 таких, что ни одна из них не является 1-й компонентой отношения R. Выражение (*) называется безопасным, если: 1) Из истинности выражения 2) Если 3) Если Пример: – имеет место для бинарных отношений и означает, что Выражения исчисления с переменными на доменах эквивалентны выражениям исчисления с переменными-кортежами. Формализуем алгоритм перевода выражений исчисления с переменными-кортежами в выражения исчисления с переменными на доменах: 1. Если 2. Атомы 3. Каждое свободное вхождение 4. Для каждого квантора
5. Выполняется построение выражения Пример: В РИ с переменными на доменах существуют 2 теоремы: Теорема: Для каждого безопасного выражения РИ с переменными-кортежами существует эквивалентное безопасное выражение РИ с переменными на доменах. Теорема: Для каждого безопасного выражения с переменными на доменах существует эквивалентное ему выражение РА.
РИ есть метод определения того отношения, которое нам желательно получить (как ответ на запрос) в терминах уже имеющегося отношения. РИ представляет собой набор правил для записи выражений, определяющих некоторое новое отношение в терминах заданной совокупности отношений.
Реляционные ЯМД. Рассмотренные РА и РИ-я могут служить основой ЯМД. Использовать РИ с переменными-кортежами как эталон для оценки ЯМД, основанный на РМ, впервые предложил Кодд. Кодд предложил язык Alpha, основанный на РИ. Этот язык является скорее абстрактным, т.к. нет систем, которые полностью бы его реализовали. DAMAS, INGRES реализовали этот язык частично. Этот язык обладает очень мощными средствами выборки: - с упорядочиванием; - с использованием - с использованием - с использованием Существуют агрегатные функции count, total, max, min, average. Count – промежуточным результатом является отношение; total – список, в котором повторяющиеся значения не удаляются. Язык Alpha является более чем полным. Язык, в котором можно (по крайней мере) моделировать исчисление с переменными-кортежами, либо, что равносильно операциям РА, или исчисление с переменными на доменах, называется полным. Т.к. реальные языки можно реализовывать функциями не имеющими аналогов ни в РА, ни в РИ; то их называют более чем полными (реальные языки, включающие навигационные операторы и процедуры БД). Такие языки включают, естественно, команды, которые не являются частью РА или РИ. Кроме того, в них возможно: 1) Арифметические вычисления. Атомы в выражениях РИ и формулах селекции в алгебраическом выражении часто могут включать арифметические вычисления, а также сравнения (+ многие другие арифметические операции не использующиеся в РА и РИ). 2) Команды присваивания и печати. 3) Агрегатные функции. К столбцам отношения часто применяют такие операции, как среднее, сумма, min, max. Часто говорят, что языки, основанные на РИ, представляют собой языки более высокого уровня по сравнению с алгебраическим, поскольку алгебра специфицирует порядок операций, в то время как исчисление оставляет определение наиболее эффективного порядка вычисления компилятору или интерпретатору.
Например, если имеются отношения
– напечатать значения Эквивалентное выражение в исчислении с переменными на доменах:
Выражение в исчислении фактически только указывает, что мы хотим, но не описывает, как это получить. (2) только специфицирует свойства желаемого значения. (1) специфицирует конкретный порядок операций. Вычисление (1) требует выполнения операции соединения, что в свою очередь может вызвать необходимость сортировки обоих отношений по их
Здесь сначала нужно найти в Выражение (3) может быть вычислено как по (1), так и по (2). Компилятор языка при оптимизационном просмотре может непосредственно преобразовать (1) в (3). Языки, основанные на РИ, в настоящее время более распространены, чем на РА.
При рассмотрении языков важным является то, насколько легко в этих языках можно реализовать операции включения, выбора, проекции и естественного соединения. Такие выражения называются выражениями вида «селекция – проекция – соединение». 1. ISBL (Information System Base Language). Используется в PRTV (Peterlee Relational Test Vehicle). Он весьма близок к РА. Соответствие операторов языка и РА:
Этот язык не содержит никаких агрегатных функций, не реализует операции включения, удаления и модификации кортежей. Но можно написать любые программы на ПЛ/1. 2. QUEL (QUEry Language) – это язык манипулирования данными системы INGRES (Interactive Graphics and Retrieval System). INGRES – полная система управления РБД, которая создана в университете шт. Калифорния и до сих пор развивается и совершенствуется. Это язык РИ с переменными-кортежами. В языке существуют возможности удаления, добавления и модификации данных, а также агрегатные функции: сумма, среднее, счетчик, min, max. 3. QBE (Query-By-Example) – язык РИ с переменными на доменах. Разработан фирмой IBM. В этом языке так же существуют операции обновления данных (удаления, добавления, модификации), агрегатные функции (обычные). Кроме этого в QBE предусмотрены возможности, которых нет в РА и в РИ. Его специфика заключается в том, что запрос формулируется путем заполнения табличной формы, содержащей имена отношений и его атрибутов. Табличная форма появляется на экране при нажатии специальных клавиш терминала (т.е. язык QBE предназначен для работы с терминалом). Для заполнения и модификации таблиц существует специальный экранный редактор. 4. SQL (Structured Query Language) – язык манипулирования данными, используемый в реляционных системах БД; в настоящее время принят за стандарт для БД. Синтаксически SQL близок к исчислению кортежей. Предшественником этого языка был язык SQUARE(создан для СУБД System-R), этот язык с одной стороны отношения напоминает РА, с другой – РИ с переменными-кортежами (можно именовать кортежи в отношениях, или сравнивать множества с помощью условия Операторы;
Оператор присваивания (<выражение> – n-компонентное отношение), вычисляется выражение и присваивается результат отношению Основной операцией в SQL является операция отображения, представляющая собой композицию выбора и проекции. Общий вид отображения:
Если Можно конструировать композиции отображений используя оператор
Язык запросов в SQL. 1. Отображение: Select A1…An from R Where B1θ1b1Ù…ÙBmθmbm Выражение, следующее за where, может содержать атрибуты отношения, арифметические операции сравнения, булевские связки and, not, or, может содержать операции над множествами (union – 1) Выражение, следующее за where может содержать операнды, которые представляют собой отношения, сформированные другим предложением select _ from _ where. 2) SQL может оперировать не только одним отношением в предложении from. На значение атрибута любого из отношений, указанных в предложении from, может ссылаться как в select, так и в where. Если А является атрибутом более одного отношения, то пишут R.А, указывая тем самым, что имеется в виду атрибут А из отношения R. При наличии в запросе предложения from R1,…,Rn будут рассматриваться все списки t1,…,tn кортежей, где tiÎRi. Если данный список удовлетворяет условиям, указанным в предложении where, в результат оператора включается список компонентов, специфицированных в предложении select. Операторы включения, удаления, модификации в SQL являются синтаксически улучшенной версией соответствующих операторов SQUARE. 2. Операция обновления: Update имя_БД Set <выражение1> Where < выражение2 > – обновление одной таблицы. 3. Операция удаления: Delete имя_БД Where В – удаляет записи БД, удовлетворяющие условию. Delete имя_БД – таблица есть, но она пустая. Все операции SQL сами открывают БД. 4. Дополнение БД. Дополняемая БД может быть не открыта, а после дополнения она остается открытой и активной. 1) Insert into <имя_БД> [(<поле1> [,<поле2> [,…]])] Values (<выражение1> [,<выражение2> [,…]]) Добавляем записи в конец существующей БД; значение <вырi> записывается в <полеi>; если <полеi> опущено, то значение <вырi> записывается в поля в соответствии со структурой.
3) Insert into <имя_БД> from array {из мн-ва} <массив> from memvar {из врем. пер-х} Временные переменные должны существовать и иметь имена полей = имени поля БД, но первая буква M. Такие переменные вырабатываются по команде Scatter memvar. 5. Операция создания БД: Create dbf <имя dbf -файла> (<имя поля> <тип> [(<размер>[,<дробный р-р>] [,<имя поля>]]) / From array <массив> ¯ массив из 4-х столбцов и строк = числу полей Тип: C,N,D,M,F,L. fix пл. точк. Массив, соответствующий описанию полей, создается функцией Afields () (при открытой БД). ЗАЩИТА БАЗ ДАННЫХ. Защита данных в БнД – это решение двух проблем: 1) ограничение целостности данных; 2) секретность данных. Проблема целостности данных заключается в обеспечении соответствия данных, хранящихся в БД, реальному текущему состоянию ПО. Логические ограничения, накладываемые на данные, называются ограничениями целостности. Ограничение целостности – это свойство, которое для данного множества или отношения либо истинно, либо ложно. Это значение должно сохраняться для каждого возможного значения, в котором находится объект. Существует 3 основных вида ограничений целостности: 1. Внутренние (структурные) – те ограничения, которые лежат в основе структуры БД. Например, РМД присуще внутреннее ограничение, что сущности и связи между сущностями представлены в виде отношений (таблиц). 2. Явные (семантические) ограничения целостности или утверждения. 3. Ограничения, вводимые на основе внутренних и явных. Это подразумеваемые. Семантические ограничения делятся на 2 вида: 1) Касается реальных значений, хранящихся в БД. Обычно такие ограничения требуют, чтобы значение атрибута принадлежало некоторому диапазону, или выражалось через какое-то арифметическое соотношение между другими атрибутами. 2) Показывает связь между атрибутами одного отношения. Записывается в виде функциональной зависимости.
Функциональные зависимости. Функциональные зависимости описывают ограничения, которые связаны не с конкретными значениями атрибута, а с тем, совпадают ли определенные компоненты кортежей. Пусть Функциональные зависимости возникают различными способами: 1) Если, например, 2) 3) Если заданы функциональные зависимости, то СУБД будет: а) поддерживать ограничения целостности; б) более эффективно будет реализовываться отношение, однако при этом будет невозможно хранение некоторой информации. Например, Имя
В связи с введением функциональной зависимости можно дать другое определение ключа: Если 1) 2) Ни для какого собственного подмножества Правила вывода называются аксиомами функциональной зависимости; пусть задана схема отношения 1˚. аксиома рефлексивности: 2˚. аксиома пополнения: 3˚. аксиома транзитивности: Пример: R (индекс, город, адрес)
город, адрес → индекс
город, адрес → индекс, город, адрес индекс, адрес → индекс, город, адрес Рассмотренные аксиомы являются надежными, т.е. приводят к истинным заключениям. Другие правила вывода, которые являются следствием из 1˚-3˚: 4˚. правило объединения: 5˚. правило декомпозиции: 6˚. правило псевдотранзитивности: Правило объединения и декомпозиции порождают важное следствие: Если Не существует алгоритма для нахождения множества функциональной зависимости.
|
|||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 372; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.243.41 (0.014 с.) |

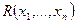 в – n-арное отношение, где
в – n-арное отношение, где  или переменной на домене. Эта запись указывает, что значения тех
или переменной на домене. Эта запись указывает, что значения тех  , которые являются переменными на доменах, должны быть выбраны так, чтобы
, которые являются переменными на доменах, должны быть выбраны так, чтобы  было кортежем отношения
было кортежем отношения  .
. ;
;  или переменные на доменах;
или переменные на доменах;  оператор сравнения;
оператор сравнения;  должны быть выбраны так, что
должны быть выбраны так, что  и кванторы
и кванторы  .
. , (*)
, (*) формула такая, что ее свободные переменные на доменах являются различными переменными
формула такая, что ее свободные переменные на доменах являются различными переменными  .
.


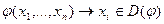 .
. подформула
подформула  , то из истинности
, то из истинности  .
. подформула
подформула  .
.
 состоит из кортежей таких, что ни один из их компонентов не является первым компонентом какого-либо кортежа отношения
состоит из кортежей таких, что ни один из их компонентов не является первым компонентом какого-либо кортежа отношения  .
. является кортежем арности n, то введем n новых переменных на доменах
является кортежем арности n, то введем n новых переменных на доменах  заменяются атомами
заменяются атомами  .
. заменяется на xi.
заменяется на xi. или
или  вводится m новых переменных на доменах
вводится m новых переменных на доменах  , где m –арность
, где m –арность  . Делаются замены:
. Делаются замены: на
на  ,
, на
на  ,
, на
на  ,
, на
на  .
. , где
, где  представляет собой
представляет собой  , в котором проведены замещения 1-4.
, в котором проведены замещения 1-4. перепишется
перепишется  .
. ;
; ;
; (получить имена тех поставщиков, которые поставляют все детали; подсчет числа кортежей в отношении).
(получить имена тех поставщиков, которые поставляют все детали; подсчет числа кортежей в отношении). и
и  мы можем записать:
мы можем записать: (1)
(1) , ассоциированные со значением
, ассоциированные со значением  , равным
, равным  , в отношении со столбцами
, в отношении со столбцами  , полученным в результате соединения.
, полученным в результате соединения. (2)
(2) значениям и просмотра отсортированных отношений. Это требует значительного времени. В зависимости от организации файлов, используемых для представления
значениям и просмотра отсортированных отношений. Это требует значительного времени. В зависимости от организации файлов, используемых для представления  , вычисление по формуле (3), эквивалентной (1), займет меньше времени:
, вычисление по формуле (3), эквивалентной (1), займет меньше времени:
 (3)
(3) значениями
значениями  . Затем находим кортежи
. Затем находим кортежи  значения.
значения.
 ).
). – как в РА;
– как в РА; ;
; ;
;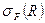 не как в РА, а в стиле исчисления с переменными-кортежами
не как в РА, а в стиле исчисления с переменными-кортежами  , где
, где 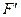 есть
есть  , в котором
, в котором  замещает атрибут
замещает атрибут  –
–  <выражение>
<выражение>
 имя отношения;
имя отношения; атрибуты
атрибуты  оператор сравнения
оператор сравнения  ;
; .
.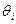 опущен, то подразумеваем “=”.
опущен, то подразумеваем “=”. (также строится соединение). Отображение воплощает в себе суть РА – “выбор-проекция-соединение”:
(также строится соединение). Отображение воплощает в себе суть РА – “выбор-проекция-соединение”: .
. , intersect – ∩, minus – /), операции принадлежности множеству (X in R, R contain X, R does not contain X, X not in S). Во всех этих операциях X – элемент множества, или кортеж, или множество.
, intersect – ∩, minus – /), операции принадлежности множеству (X in R, R contain X, R does not contain X, X not in S). Во всех этих операциях X – элемент множества, или кортеж, или множество. – схема отношения, а
– схема отношения, а  – подмножества
– подмножества  , если в любом отношении R не существует 2-х кортежей, компоненты которых совпадают по всем атрибутам, принадлежащим
, если в любом отношении R не существует 2-х кортежей, компоненты которых совпадают по всем атрибутам, принадлежащим  , но не совпадают по одному или более атрибутам, принадлежащим Y.
, но не совпадают по одному или более атрибутам, принадлежащим Y.  .
. –
–  набора объектов
набора объектов  к набору
к набору  . Среди
. Среди  есть атрибуты, образующие ключ
есть атрибуты, образующие ключ 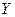 для
для  для
для  .
. Телефон; то не может быть 2-х телефонов для одного человека.
Телефон; то не может быть 2-х телефонов для одного человека. – схема отношения с атрибутами
– схема отношения с атрибутами  и множество функциональных зависимостей
и множество функциональных зависимостей  подмножество
подмножество  , где
, где  – замыкание множества функциональных зависимостей;
– замыкание множества функциональных зависимостей; . F+ – все функциональные зависимости, которые могут быть получены для данного отношения с использованием правил вывода.
. F+ – все функциональные зависимости, которые могут быть получены для данного отношения с использованием правил вывода.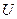 и множеством функциональных зависимостей
и множеством функциональных зависимостей  Это правило дает тривиальные зависимости, т.е. зависимости, правая часть которых содержится в левой части. Его использование не зависит от
Это правило дает тривиальные зависимости, т.е. зависимости, правая часть которых содержится в левой части. Его использование не зависит от 

 F: индекс → город
F: индекс → город F+: индекс, адрес → город, адрес
F+: индекс, адрес → город, адрес
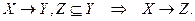 (вытекает из 1˚, 3˚).
(вытекает из 1˚, 3˚).
 – атрибуты, то зависимость
– атрибуты, то зависимость  справедлива т. и т.т., когда
справедлива т. и т.т., когда  .
.


