
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Декомпозиция схем отношений.
Декомпозиция схем отношений является важным элементом проектирования БД. Декомпозицией схемы отношений 1) свойство соединения без потерь:
где Метод, проверяющий сохраняется ли свойство соединения без потерь: Строится таблица с n столбцами и k строками. Столбец j соответствует атрибуту Повторно рассматриваем каждую из зависимостей После модификации строк таблицы может обнаружиться, что некоторая строка стала равной Пример:
– декомпозиция обладает свойством соединения без потерь. 2) множество зависимостей Формально проекцией Это следует из того, что Может выполняться только одно из свойств. Декомпозиция может сохранять Для того чтобы привести схему отношения к какой-то декомпозиции существуют алгоритмы.
НОРМАЛИЗАЦИЯ ОТНОШЕНИЙ. При проектировании БД возможно возникновение проблем избыточности и аномалий при выполнении операций включения, удаления и обновления данных. Пример: Поставщик (ФИО; номер; адрес; товар; количество) Избыточность: если разный товар поставляется одним и тем же поставщиком, то его адрес повторяется всякий раз. Þ Обновление: если изменяется адрес поставщика, то его надо менять во всех кортежах; если этого не случится, то у поставщика будут разные адреса. Удаление: если в данный момент прекратил поставлять товар, то его адрес утрачивается. Включение: не может быть включена запись о поставщике, не поставляющем в данный момент товар. Все проблемы исчезают, если заменить это отношение двумя: Поставщик (ФИО; номер; адрес) Поставка (номер поставщика; товар; количество) Такая схема получается в результате нормализации отношений. Введены 4 уровня нормализации схем отношений, которые называются соответственно 4-мя нормальными формами: 1НФ: Схема отношений 1НФ достаточна для рассматриваемых языков запросов. 2НФ: Если Схема отношений 3НФ: Транзитивная зависимость. Для данной схемы отношений
Схема отношений находится в 3НФ относительно множества функциональных зависимостей Любая схема отношений, находящаяся в 3НФ относительно НФБК: (Бойса-Кодда) Схема отношений Схема отношений может быть в 3НФ, но не быть при этом в НФБК; но если отношение находится в НФБК, то всегда находится в 3НФ. Для приведения схем отношений в НФБК существуют алгоритмы, использующие декомпозицию, обладающую свойством соединения без потерь (сохраняющей зависимость может иметь место и не иметь). Пример: номер поставщика → товар
– 2НФ
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 646; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.39.32 (0.014 с.) |
 называется замена ее совокупностью схем
называется замена ее совокупностью схем  подмножеств
подмножеств  таких, что
таких, что  ; не обязательно
; не обязательно  При построении декомпозиции желательно выполнение двух свойств:
При построении декомпозиции желательно выполнение двух свойств: ,
,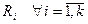 .
. , а i-я строка отношению
, а i-я строка отношению  . На пересечении строки i и столбца j поместим символ aj, если
. На пересечении строки i и столбца j поместим символ aj, если 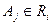 . В противном случае туда поместим символ bij.
. В противном случае туда поместим символ bij. в
в  до тех пор, пока в таблице невозможно будет сделать какие-либо изменения. Всякий раз, рассматривая зависимости
до тех пор, пока в таблице невозможно будет сделать какие-либо изменения. Всякий раз, рассматривая зависимости  . Тогда декомпозиция обладает свойством соединения без потерь. В противном случае она не обладает таким свойством.
. Тогда декомпозиция обладает свойством соединения без потерь. В противном случае она не обладает таким свойством.

 таких, что
таких, что 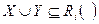 (
( ). Будем говорить, что декомпозиция сохраняет множество зависимостей
). Будем говорить, что декомпозиция сохраняет множество зависимостей  логически следуют все зависимости, принадлежащие
логически следуют все зависимости, принадлежащие 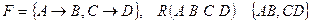 . И, наоборот.
. И, наоборот. находится в 1НФ т. и т.т., когда все входящие в нее атрибуты являются атомарными (неделимыми).
находится в 1НФ т. и т.т., когда все входящие в нее атрибуты являются атомарными (неделимыми). – ключ отношения
– ключ отношения  непервичный атрибут отношения
непервичный атрибут отношения  ),
),  первичный атрибут, если он является элементом какого-либо ключа отношения
первичный атрибут, если он является элементом какого-либо ключа отношения  и
и  . Если это условие не выполняется, то говорят, что атрибут
. Если это условие не выполняется, то говорят, что атрибут  функционально полно зависит от
функционально полно зависит от  .
. , атрибута
, атрибута  такое, что
такое, что 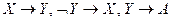 относительно
относительно  .
.

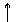

 ФИО, адрес → товар
ФИО, адрес → товар



 номер поставщика → индекс товара
номер поставщика → индекс товара 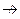 товар - 3НФ
товар - 3НФ


