
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритм1: пополняющий декомпозицию схем отношений, которая обладает свойством соединения без потерь и приводит к отношениям находящимся в нфбк.Содержание книги
Поиск на нашем сайте
Входные данные: схема отношения Выходные данные: декомпозиция Метод: декомпозиция
Тогда в Декомпозиция
Алгоритм 2: приведения отношения к 3НФ, использующей декомпозицию, сохраняющую функциональные зависимости. Входные данные: схема отношения Выходные данные: сохраняющая зависимости декомпозиция схемы отношения Метод: если существует некоторый атрибут в Теорема: Пусть Пример:
В декомпозицию будут входить
МНОГОЗНАЧНЫЕ ЗАВИСИМОСТИ. Кроме рассмотренных функциональных зависимостей существует другой вид зависимости – многозначная. Пусть задана схема отношений
Из симметрии определения
X Y Z
|
||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 209; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.77.244 (0.008 с.) |

 и функциональные зависимости
и функциональные зависимости  .
. , обладающая свойством соединения без потерь, такая, что каждая схема отношения в декомпозиции находится в НФБК относительно проекции
, обладающая свойством соединения без потерь, такая, что каждая схема отношения в декомпозиции находится в НФБК относительно проекции  для
для  . Существует ключ
. Существует ключ 
 . Если
. Если  схема отношения из
схема отношения из  не находится в НФБК, то пусть
не находится в НФБК, то пусть  – зависимость, имеющая место в
– зависимость, имеющая место в  не содержит ключа
не содержит ключа  .
. и не принадлежит
и не принадлежит 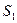 и
и 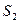 , где
, где  и
и  . (это удаление транзитивной зависимости
. (это удаление транзитивной зависимости  .
. . Т.к. в
. Т.к. в  для каждой зависимости
для каждой зависимости  , то может быть использована схема
, то может быть использована схема 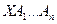 вместо
вместо  , и такая подстановка является предпочтительной.
, и такая подстановка является предпочтительной. ключ
ключ 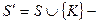 декомпозиция
декомпозиция 



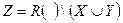 . Существует
. Существует  (X мультиопределяет Y) – многозначная зависимость, если:
(X мультиопределяет Y) – многозначная зависимость, если:
 и
и  следует, что в
следует, что в  :
: .
.


 t1
t1

 t2
t2


