
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Реляционное исчисление с переменными-кортежами.Содержание книги
Поиск на нашем сайте
Аналогично тому, как РА использует в качестве операндов отношения, РИ кортежей строит свои выражения из кортежей. Выражение в РИ строятся из атомов. Атомы могут быть трех типов: 1) 2) 3) ti θС, Сθti, где
Переменная называется связанной, если этой переменной в формуле предшествует квантор Выражение определяется рекурсивно следующим образом: 1) Каждый атом является выражением. Переменные в выражении являются свободными или связанными в зависимости от того, были ли они свободными или связанными в атоме. 2) Если φ1 и φ2 – выражения РИ, то φ1 3) Если φ – формула, то 4) Если φ – формула, то 5) Формулы могут заключаться в скобки. Если их нет, то приоритет операций: 6) Ничто другое не является формулой. Таким образом, формула в РИ с переменными-кортежами есть выражение вида Пример:
РИ с переменными-кортежами в том виде, в каком его определили, позволяет представить некоторые бесконечные отношения. Например, D(φ) - множество символов, которые явно появляются в выражении φ, либо являются компонентами какого-либо кортежа отношения
Rj имеет nj компонент, Выражение 1. Всякий раз, когда кортеж t удовлетворяет выражению φ, каждая компонента кортежа t принадлежит множеству D(φ). 2. Для любого подвыражения вида 3. Если для любого подвыражения вида Условие 3 может показаться не интуитивным, но мы должны заметить, что формула Пример безопасного выражения: Пусть
т.к. любое Обобщения: безопасным является выражение:
На основании приведенных условий можно утверждать, что если Если φ состоит из подвыражений φ1 и φ2, связанных связками Безопасные выражения РИ с переменными-кортежами эквивалентны РА. Теорема: Если существует выражение РА, то существует эквивалентное ему безопасное выражение в РИ с переменными-кортежами.
|
||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 339; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.01 с.) |

 , где
, где  – имя отношения, а
– имя отношения, а  – переменная-кортеж. Этот атом означает, что
– переменная-кортеж. Этот атом означает, что  , где
, где  и
и  – переменные-кортежи,
– переменные-кортежи,  – арифметический оператор сравнения;
– арифметический оператор сравнения;  – номера столбцов кортежей
– номера столбцов кортежей  -й компонент
-й компонент  -й компонентой
-й компонентой  – то же, что в 2); С =
– то же, что в 2); С =  . Этот атом означает, что
. Этот атом означает, что  или
или  . В противном случае переменная называется свободной.
. В противном случае переменная называется свободной. φ2, φ1
φ2, φ1  φ2, φi – также выражения РИ. В результирующем выражении переменные будут свободными или связанными так же, как они были свободными или связанными в выражениях φ1 и φ2.
φ2, φi – также выражения РИ. В результирующем выражении переменные будут свободными или связанными так же, как они были свободными или связанными в выражениях φ1 и φ2. – формула, которая утверждает, что существуют значения
– формула, которая утверждает, что существуют значения  , при подстановке которых вместо всех свободных вхождений переменной
, при подстановке которых вместо всех свободных вхождений переменной  , эта формула становится истинной. Переменная
, эта формула становится истинной. Переменная  – формула. Эта формула утверждает, что какое бы значение подходящей арности мы не подставляли вместо свободных вхождений
– формула. Эта формула утверждает, что какое бы значение подходящей арности мы не подставляли вместо свободных вхождений 
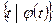 , где
, где 
 означает все возможные не принадлежащие
означает все возможные не принадлежащие  , должен быть элементом множества
, должен быть элементом множества  .
. является функцией отношений, которые должны подставляться вместо переменных отношения в
является функцией отношений, которые должны подставляться вместо переменных отношения в 
 – множество констант.
– множество констант. , входящего в выражение
, входящего в выражение  , если t удовлетворяет
, если t удовлетворяет  .
. , входящего в выражение
, входящего в выражение  , то t будет удовлетворять выражению
, то t будет удовлетворять выражению 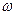 .
. . Последняя является безопасной, если
. Последняя является безопасной, если 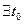 для которого истинно
для которого истинно 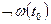 и
и  . Домены
. Домены  одни и те же, следовательно, условие 3 устанавливает, что формула
одни и те же, следовательно, условие 3 устанавливает, что формула  безопасна, когда безопасна формула
безопасна, когда безопасна формула 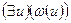 и
и 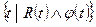 (*),
(*), . Например, такой вид имеет формула разности множеств:
. Например, такой вид имеет формула разности множеств:  при
при  .
.

 должны быть символом, появляющемся в
должны быть символом, появляющемся в  -ом компоненте кортежа из
-ом компоненте кортежа из  . Такой вид имеет проекция
. Такой вид имеет проекция .
. выражения (*).
выражения (*).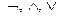 , и каждое φi может быть определено правилами 1-3, то безопасность выражения φ определяется безопасностью выражений φ1 и φ2.
, и каждое φi может быть определено правилами 1-3, то безопасность выражения φ определяется безопасностью выражений φ1 и φ2.


