
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальні принципи побудови системСтр 1 из 28Следующая ⇒
Загальні принципи побудови систем Класифікації систем Системи розділяють на класи по різних ознаках, і в залежності від розв'язуваної задачі можна вибирати різні принципи класифікації. Починалися спроби класифікувати системи по виду відображуваного об'єкта (технічні, біологічні, економічні і т.п. системи); по виду наукового напрямку, використовуваного для їхнього моделювання (математичні, фізичні, хімічні й ін.). Системи поділяють на детерміновані і стохастичні, відкриті і закриті; абстрактні і матеріальні (тобто існуючі в об'єктивній реальності) та ін. Класифікації завжди відносні. Так, у детермінованої системі можна знайти елементи стохастичності, і, навпаки, детерміновану систему можна вважати окремим випадком стохастичної (при ймовірності, рівній одиниці). Аналогічно, якщо взяти до уваги діалектику суб'єктивного й об'єктивного в системі, то стане зрозумілою відносність поділу системи на абстрактні й об'єктивно існуючі: це можуть бути стадії розвитку однієї і тієї ж системи. Дійсно, природні і штучні об'єкти, відбиваючись у свідомості людини, виступають у ролі абстракційних понять, а абстрактні проекти створюваних систем втілюються в реально існуючі об'єкти, які можна відчути, а при вивченні знову відобразити у вигляді абстрактної системи. Однак відносність класифікацій не повинна зупиняти дослідників. Ціль будь-якої класифікації - обмежити вибір підходів до відображення системи, поставити у відповідність виділеним класам прийоми і методи системного аналізу і дати рекомендації відносно вибору методів для відповідного класу систем. При цьому система, в принципі, може бути одночасно охарактеризована декількома ознаками, тобто вона може займати місце одночасно в різних класифікаціях, кожна з яких може виявитися корисною при виборі методів моделювання. Розглянемо для прикладу деякі з найбільш важливих класифікацій систем. Відкриті і закриті системи. Поняття відкритої системи ввив Л. фон Берталанфі. Основні характерні риси відкритих систем - здатність обмінюватися із середовищем масою, енергією й інформацією. На відміну від них закриті чи замкнуті системи передбачаються (зрозуміло, з точністю до прийнятої чутливості моделі) цілком позбавленими цієї властивості, тобто ізольованими від середовища.
Можливі окремі випадки: наприклад, не враховуються гравітаційні й енергетичні процеси, а відображається в моделі системи тільки обмін інформацією із середовищем; тоді говорять про інформаційно-проникні чи відповідно про інформаційно-непроникні системи. Одна з найбільш важливих особливостей відкритих систем полягає в наступному. У відкритих системах виявляються так звані термодинамічні закономірності, що здаються парадоксальними і суперечать другому початку термодинаміки. Нагадаємо ще раз, що другий закон термодинаміки (так зване "друге начало"), сформульований для закритих систем, характеризує систему зростанням ентропії, прагненням до невпорядкованості, руйнування. Виявляється цей закон і у відкритих системах (наприклад, старіння біологічних систем). Однак на відміну від закритих у відкритих системах можливе введення упорядкованості (зниження ентропії); подібні системи можуть зберігати свій високий рівень і навіть розвиватися убік збільшення порядку складності, тобто в них виявляється так звана закономірність самоорганізації, що розглядатиметься трохи далі. Саме тому важливо для систем управління підтримувати обмін інформацією із середовищем. Цілеспрямовані системи. Як уже відзначалося, не завжди при вивченні систем можна застосовувати поняття мета системи. Однак при вивченні економічних, і організаційних об'єктів доцільно і важливо виділяти також класі цілеспрямованих систем. У цьому класі, в свою чергу, можна виділити системи, у яких цілі задаються ззовні (звичайно це має місце лише в закритих системах), і системи, у яких цілі формуються усередині системи (що характерно для відкритих, систем які мають властивість самоорганізації). Критерії оптимізації систем Серед задач, що виникають у зв'язку із створенням систем, можна виділити задачі 2-х видів: - задачі аналізу, що пов'язані з вивченням властивостей функціонуванням системи в залежності від структури і значень збурюючи: і керуючих дій. Кінцевою метою аналізу є, як правило, судження про якість функціонування існуючої (або спроектованої) системи у заданих умовах впливу навколишнього середовища.
- задачі синтезу, що зводяться до вибору елементів (або зв'язків між ними або режимів їх функціонування) системи, що проектується, які забезпечують задані показники якості функціонування системи у заданих умовах впливу навколишнього середовища. Кінцевою метою синтезу, як правило, є набір елементів, зв'язків між ними і параметрів елементів нової створеної системи з метою забезпечення заданої поведінки цієї системи. Показники якості функціонування системи Для оцінки поведінки системи використовують певні критерії оцінки у вигляді деяких функціоналів. Розглянемо в якості прикладу транспортну систему міста, в якій для покращення роботи транспорту можуть бути використані наступні види організаційного управління: х1 - збільшення транспортних одиниць на мережі для перевезення вантажів і пасажирів; х2 - збільшення пропускної здатності міських магістралей; х3 - варіації вантажопід'ємності та пасажиромісткості міського транспорту.; х4 - інженерне облаштування вулиць та шляхів. Необхідно визначитись щодо ефективності та доцільності того або іншого виду організаційного управління. Нехай W - показник ефективності системи (наприклад, прибуток від виконання перевезень вантажів і пасажирів), W1;W2; W3; W4- той же самий показник, що відповідає обраному управлінню (х1 х2, х3, х4). Тоді величина різниці ΔW1,2 = W1 - W2 - може бути оцінкою порівняння ефективності варіанту управління х1 у порівнянні з варіантом х2. Очевидно, що можна оцінювати і комплексне управління. Наприклад, значення ΔW1,2,3 = W1,2 - W3 дозволяє оцінювати ефективність впровадження комплексу управлінь х1 х2 У порівнянні з одним лише управлінням х3 і т.п. У загальному випадку, для того щоб знайти глобальний оптимум показника W (найефективніше управління), зазвичай вирішують задачу оптимізації W шляхом варіювання значень управлінь х1 х2... хn. Загальний показник ефективності W залежить від трьох категорій факторів: - фактори α1; α2;... - які попередньо відомі чи можуть контролюватися у процесі функціонування системи. - невідомі (або ті, що не можуть бути виміряні кількісно) фактори Y1, Y2… - можливі елементи рішення X1, Х2,...- які ми маємо обирати. Тоді можна записати у загальному вигляді певний функціонал, що відображає вплив усіх цих факторів на ефективність функціонування системи: W = W(α1; α2; ... Y1 ;Y2...; X1; Х2...) (1.1) У найпростішому вигляді, коли немає невідомих факторів Y1 ;Y2... вказаний функціонал приймає вид: W = W(α1; α2; ... X1; Х2...) (1.2) Якщо ця залежність має місце, то задача аналізу системи може бути сформульована наступним чином. При заданих зовнішніх умовах α1; α2;... і обраних управліннях X1; Х2... знайти чисельне значення показника ефективності W. Очевидно, що при коректно отриманій залежності задача аналізу зводиться до чисто обчислювальних процедур. Очевидно, також, що можна змінювати значення або аі або Xі і оцінювати кожного разу нове значення W. При вирішенні задачі синтезу за допомогою функціонала (1.2) задач визначення оптимальних значень Х1;Х2... можна сформулювати наступним чином. При заданих умовах α1; α2;... знайти такі елементи вирішення X1;Х2..., які перетворюють W в максимум.
Це типова математична задача, що відноситься до класу так званим варіаційних задач, вирішення яких достатньо добре відомо інженерам: - для знаходження max (або тіп) W необхідно продиференціювати вираз (1.2) по аргументу Xі (чи по аргументам, якщо їх декілька» прирівняти добуток до нуля і вирішити отриману систему рівнянь. Відмітимо, що у випадку наявності обмежень на варіації Xі екстремум отримати на заданому інтервалі не завжди вдається, тоді він лежить, як правило, на межі області можливих значень рішень. У будь-якому випадку, при відсутності неконтрольованих факторів Y1 Y2... пошук оптимуму представляє, частіше за все, лише проблему, яка обчислюється і вирішується з залученням ідей лінійного чи нелінійного програмування (про це ми поговоримо більш докладно трохи пізніше). Якщо ж існують фактори, що є неконтрольованими, і функціонал визначається формулою (1.1), проблема вибору оптимальних управлінь X1 Х2...суттєво ускладнюється. Це вже не лише математична задача. Наявність Y1 Y2... y виразі (1.1) приводить задачу оптимізації до задачі про вибір рішення в умовах невизначеності. Будемо чесними: невизначеність - є невизначеністю. Будь-яке рішення прийняте в умовах невизначеності завжди гірше рішення, прийнятого у досить визначеній ситуації. Але ж рішення, прийняте в умовах визначеності на основі математичних розрахунків і прогнозів, як підтверджує практика, все ж краще рішення, прийнятого навмання. Природнім і розумним виявляється вивчення передісторії зміни неконтрольованих факторів Yi (і є N), наприклад, визначенням ймовірності того чи іншого чисельного значення цих факторів. У гіршому випадку, можна просто по передісторії визначити їх середнє значення і використати їх у функціоналі (1.1) як відомі величини, привівши задачу до класу детермінованих варіаційних задач. У випадку, коли Yi (і є N) є випадковими величинами для оптимізації може бути застосовано один з двох прийомів: 1. Штучне зведення задачі до детермінованої схеми, коли варіації Yi, відносно його математичного сподівання M(Yi) дуже малі і можна у розрахунках прийняти саме їх середні значення. 2. Здійснювати оптимізацію "вручну", тобто враховувати закони розподілу випадкових змінних Yi (і є N) і оцінювати середнє значення показника ефективності у відповідності з формулою:
Особливий клас задач оптимізації складних систем представляє випадок наявності конфліктних ситуацій, коли Yi (і є N) залежить не стільки від об'єктивних обставин, а від активно протидіючого розробнику системи конкурента. Така ситуація частіш за все виникає при управлінні збутом продукції в умовах ринку. В цьому випадку для прийняття оптимальної стратегії управління застосовують так звану теорію ігор, що займається саме обґрунтуванням прийняття рішень у конфліктних ситуаціях.
Відмітимо також дуальність задач оптимізації, що полягає у можливості пошуку або max функціонала, або тіп деякого іншого функціонала, що виражається через функціонал, що максимізується. Наприклад, замість того, щоб шукати max W, можна шукати
W'=(A-W) =>min
де А - деяка константа, до якої прагне функціонал W. Часто заміна задачі пошуку max задачею пошуку тіп здійснюється простою заміною:
W'=-W, a6o W' = l/W
Іноді оцінка якості функціонування систем здійснюється за декількома показниками, причому деякі з них необхідно максимізувати, інші - мінімізувати. Наприклад, система організації перевезень може бути охарактеризована наступними показниками: W1 - чистий прибуток від перевезень (=>тах); W2 - об'єм перевезень (=>тах); W3 - собівартість перевезень (=> тіп). У подібних випадках критерії, що є у протиріччі один одному, намагаються об'єднати у один комплексний критерій. Існують декілька прийомів запису комплексних критеріїв: 1. Узагальнений критерій:
де W1... Wm - показники, які бажано збільшити; Wm+1... Wk - показники, які бажано зменшити. Очевидно, що у даному випадку необхідно шукати max U (або навпаки, U' = 1/U=> тіп). 2. Зважений критерій.
U =a1 W1+ a2W2+... +ak∙Wk,
де a1 (і є k) - коефіцієнти важливості (впливу) і -го показника. При цьому аі можуть бути як додатні (при пошуку max) так і від'ємні (при пошуку тіп). Але обидва ці критерії мають один загальний недолік, який полягає у тому, що суттєві збитки по одному з показників (недопустимі) можуть бути скомпенсовані виграшами по інших (Як висловився Наполеон: "Ще одна така перемога - і ми програємо війну!"). Тому на практиці використовують як критерій оптимізації один, найбільш вагомий показник ефективності системи (наприклад, W1, а інші розглядаються як обмеження при пошуку його оптимального значення. W1=W1{ a 1; a 2...Y1;Y2;....X1;X2...}=>max(min),
при умові: Wіі Wіj де Наприклад, у розглянутому раніше випадку можна вимагати забезпечення Wі =>тах (максимізувати прибуток), але W2і
Програмування (ДП) Визначення методу ДП Динамічне програмування являє собою математичний метод оптимізації систем, функціонування яких представляє певну низку багатокрокових операцій (навпаки, ЛІТ призначено для пошуку оптимуму саме однокрокових операцій). Уявимо собі, що досліджувані операції являють собою процес, що розвивається в часі і який розділяється на ряд «кроків». Наприклад, економічна діяльність підприємства (Q) протягом ряду років планується й оптимізується на кожний рік, що є природним кроком розвитку підприємства. Природно, що керування діяльністю підприємства буде складатися з елементарних «крокових» управлінь, сукупність яких називається стратегією управління.
Нехай на початку періоду, що розглядається, на розвиток системи підприємств, які виконують певні функції виробництва одного виду продукції, виділені деякі кошти К0. Ці кошти повинні бути розподілені між підприємствами. У процесі функціонування ці кошти частково витратяться (тобто амортизуються). Крім того, кожне підприємство приносить доход, що залежить від вкладених коштів. На початку кожного наступного року наявні кошти, що залишилися, можуть знову якось розподіляться між підприємствами. Постає питання: як потрібно розподіляти кошти між підприємствами на протязі кожного року, щоб сумарний доход від усіх систем підприємств на період Т, був максимальним. Саме це є типовою задачею ДП. Перерозподіл коштів на початок кожного року і представляє поточний крок управління. Нехай на початку і- го року підприємствам П1, П2, … Пк виділені відповідні кошти:
(k - му підприємству в i - й рік).
Сукупність цих значень являє собою не що інше, як крокове Управління на i -му кроці:
Керування ж системою підприємств за період Т, що містить m кроків фоків) являє собою сукупність
і являє собою стратегію управління. Ефективність цієї стратегії на і-му кроці визначається показник ефективності (наприклад, отриманим доходом):
Тоді за весь період Т (за т - кроків) показник ефективності визначається як
Згідно з типовою задачею ДП необхідно вибрати стратегію управління усіма к підприємствами на і - му кроці:
що забезпечує z = zmax. Поставлену задачу можна вирішити по різному: - відразу знайти оптимальне рішення и (для оптимальної стратегії приймемо її позначку маленькою буквою и); - на кожнім і- -му кроці будемо оптимізувати тільки відповідно управління (ui), у результаті такого розгляду т кроків знайдена оптимальна стратегія.
при якій
Здавалося б рішення тривіальне: необхідно оптимізувати крок управління ui щороку (це просто, із застосуванням ЛП) і в результат оптимізації всіх кроків одержимо оптимальну стратегію управління и. Але принцип ДП аж ніяк не припускає, що кожен крок оптимізується окремо, незалежно від інших. Навпаки, крокове управління повинно вибиратися з урахуванням усіх його наслідків у майбутньому. Цей принцип сформульований американським вченим Робертом Беллманом говорить, що незалежно від того, який стан системи і яке прийнято рішення в початковий момент, наступні рішення і отже поводження системи має бути оптимальним з урахуванням саме майбутніх наслідків. Однак з цього загального правила є одне єдине виключення: останній крок, який може просто плануватися як оптимальний у рамках ЛП (без урахування наслідків), і який має приносити безумовно максимальну вигоду. Таким чином, спланувавши цей останній крок, можна до нього пристроювати передостанній, потім передпередостанній і т.д. до початкового кроку. Саме тому процес ДП розвертається, як правило, від кінця до початку. Але як же це спланувати, не знаючи передостаннього? Очевидно, потрібно зробити певні припущення щодо результатів передостаннього (т- 1)-го кроку і для нього знайти таке управління, що забезпечить максимальний виграш на останньому m -му кроці. Нехай це процедура виконання для кожного з можливих станів системи на (т-1) кроці і для кожного з них ми знаємо оптимальне керування на т-му кроці. Тепер ми можемо оптимізувати керування на (т- 1) кроці, зробивши всі можливі припущення щодо стану системи на (т-2)-у кроці. Для кожного з цих припущень знаходимо оптимальний вектор управління um-1. Іншими словами, на кожнім i -у кроці шукається управління иІ9 яке забезпечує оптимальне продовження процесу на (i +1) - кроці відносно досягнутого стану на i -му кроці. Управління, що забезпечує оптимальне продовження процесу називається умовним оптимальним управлінням на даному кроці (УОУ). Тепер припустимо, що УОУ на кожному кроці нам відомо: ми знаємо як йти далі, у якому би стані не був процес до початку кожного кроку. Тоді, якщо початковий стан S0 нам відомий, то ми знаємо, як знайти вже не умовне, а дійсно оптимальне управління на 1-му кроці. Потім, спираючись на нього, можна знайти оптимальне управління на другому кроці і т.д. У результаті ми прийдемо до кінцевого стану Sm і знайдемо оптимальний вектор управління u, що забезпечить оптимальне протікання процесу протягом усіх т кроків управління. Таким чином, при оптимізації систем методом ДП багатокроковий процес проходить двічі: - від кінцевого кроку до початкового, при цьому знаходяться оптимальні умовні управління; - від початкового кроку до кінцевого, при цьому знаходяться серед множини умовних оптимальних управлінь уже реальні оптимальні управління на кожному кроці з урахуванням результатів попереднього кроку (як початкові умови наступного). Розглянемо декілька прикладів застосування методу ДП. Задачі розподілу ресурсів При рішенні подібних задач широко використається ДП. Словесно ми вже описали алгоритм рішення. Спробуємо формалізувати і вирішити вказану задачу, спираючись на алгоритм ДП [12]. Припустимо, що на розвиток АТП відпущена певна сума коштів К, яку необхідно розподілити між двома АТП. Ефективність вкладення коштів у перше підприємство оцінюється коефіцієнтом річного прибутку α, у друге - β, причому α < 1 і β<1 і дорівнюють відповідно α=0,4 β =0,5. Наприкінці кожного року відбувається зменшення первісної суми законом φ((х)=γх; φ(у)=θу, γ=0,8; θ=0,75 (х - сума капіталовкладень у перше підприємство, у - в друге). Суми, що залишилися, наприкінці кожного року заново перерозподіляються. Обумовимо також, що сума, що залишилася наприкінці кожного року до прибутку не додається. Необхідно знайти такий розподіл капіталовкладень в перше та в друге підприємство, при якому досягається максимальна сума прибутку за всі 5 років. Неважко уявити, що поставлена задача є класичною задача оптимізації багатокрокових процесів, саме яку доцільно вирішувати застосуванням ДП. Рішення
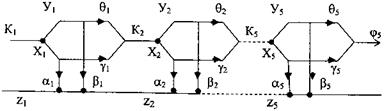
Представимо функціональну модель задачі у наступному вигляді (рис.7.2).
Рис.7.2 Функціональна модель задачі ДП Вузловими крапками моделі є крапки розподілу суми коштів Kі між підприємствами. Практично це початок кожного календарного року. Таких кроків буде 5. Далі для спрощення виразимо уі через хі тобто уі = кі — хі. Записуємо функцію переходу ψі виграш z і для кожного з етапі починаючи, як це витікає з методу ДП, з п'ятого (останнього) етапу. Етап 5 З огляду на те, що у5=к5-х5 і враховуючи а=0,4 β=0,5 γ=0,8 θ=0,75 запишемо рівняння переходу:
ψ5=γх5+ θу5=(γ-θ)х5+θК5=0,05х5+0,75К5
За умовою цей залишок у прибуток не включається. Величина отриманого прибутку протягом цього року:
z5=αx5+βy5=(α-β)x5+βx5=-0,1x5+0,5y5.
Шукаємо максимум цього прибутку: Z5 =max [-0,1х5+0,5у5]=0,5К5, якщо х5=0, у5=К5. Етап 4. Робимо аналогічні дії:
ψ4=γх4+θу4=(γ-θ)х4+θК4=0,05х4+0,75К4=К5,
оскільки це те, що залишилося після 4го року). z4=αx4+βy4=z5max=(α-β)x4+βK4+z5max,
тому що прибуток за четвертий рік додається до прибутку 5-го року. Враховуючи, що z5max=0,5K5:
Z4=max (-0,1x4+0,5K4+0,5K5).
Підставимо значення К5 і отримаємо для сумарного прибутку за 4-й і 5-й роки:
Z4=max [-0,1х4+0,5К4+0,5(0,05х5 +0,75К4)] (при 0<х4<К4)→ Z4=max [0,875К4 - 0,095х4] → Z4max=0,875К4,
якщо х4=0 і у4-К4
Етап 3. ψ3=К4=0,05х3+0,75К3 z3=(α -β)х3+βу3+z4тах. З урахуванням, що z4max=0!87 5 К4 одержимо:
Z3=(-0,1x3+0,5K3+0,875K4). Враховуючи К4=0,05х3+0,75К3, одержимо: Z3=(1,1K3+ 0,02х3) ( при 0<х3<К3) → Z3max,=1,12K3,
якщо х3=К3 (максимально можливе значення) y3=0/ Етап 2. Робимо як завжди: ψ2=К3=0,05х2+0,75К2; z2=0,4x2+0,5(K2-x2)+z3max → Z2Max = мах [1,34до2 - 0,044x2] (при 0<х2<К2) → Z2max,=1,34K2,
якщоx2=0 і y2=K2 Етап 1. По аналогії з попередніми етапами: ψ 1=0,05x1+0,75K1=K2 z1=0,4xi+0,5(K1-x1)+z2max Z1max=max[1,505K1 - 0,023x1] (npu 0<x1< K1) → Z1max=1,505K}=1,505K,
при х1=0 і у1=К (тому що K1=K). Отже: максимальний прибуток діяльності 2-х підприємств за 5 років буде дорівнювати 1,505 від суми первісного вкладення, якщо на 1 і 2 роки усю суму капіталовкладень вкладати в друге підприємство, на 3-му році в перше, а на 4 і 5 роках - знову в друге підприємство. Така стратегія оптимального управління розвитком 2х підприємств. Досі ми розглядали простий випадок, коли αі β однакові для всіх етапів. Зустрічаються задачі, де αі β на кожному етапі різні (це є задача розподілу ресурсів з неоднорідними етапами). Рішення цієї задачі практично не відрізняється від розглянутої раніше і вирішується аналогічно із застосуванням поточних значень α i і βi на кожному i -му розвитку підприємства. Зустрічаються також задачі розподілу ресурсів, коли отриманий прибуток відчисляється не повністю, а частково вкладається в розвиток виробництва. У цьому випадку відрахований прибуток на будь-якому і -мукроці записується у виді:
Zimax=max[αxi+β (Кi – xі] - r[αхі+β(Кi-xi)],
де r - коефіцієнт, який характеризує частину прибутку, що вкладається розвиток виробництва. Основне функціональне рівняння при цьому приймає вид: Zimax=max[αxi+β (Кi – xі) - r[αхі+β(Кi-xi))+Z(i+1)max]. при 0≤ xi ≤ Кi.
В подальшому процедура рішення залишається незмінною. Якщо розглядається задача розподілу ресурсів між п об'єктами господарської діяльності, то приходиться на кожнім кроці мати п оптимальних рішень (але не 2, як ми розглядали). Тоді ui =(xi(1), xi(2)…… xi(n)) – вектор вкладень в підприємства на початок і-го року. Процес пошуку оптимальної стратегії управління вкладеннями на кожному кроці також зважується поетапно. Стан системи перед початком кожного етапу як і раніше буде характеризуватися одним числом (Кi) ( Необхідно виконати наступні умови на i -му кроці:
При цьому основне функціональне рівняння матиме вид:
Це вже класична задача ЛП, розв'язання якої вже розглядалося у попередньому розділі, що має вирішуватися для кожного i -го кроку. Досить часто в практиці приходиться вирішувати задачу розподілу ресурсів із вкладенням прибутку в розвиток виробництва. Подібні задачі називаються виродженими. Особливістю їх є те, що вони вирішуються з першого до останнього кроку, (тільки вперед), що значно спрощує процедуру рішення. Наприклад, для закупівлі устаткування 2-х типів, виділена сума 20000грн.. Ефективність вкладення цих засобів в устаткування оцінюється тим прибутком, що одержить підприємство, використовуючи це устаткування. Нехай для устаткування 1-го типу коефіцієнт ефективності (прибутку) складає Ставиться задача знайти оптимальний розподіл коштів для їх ^купівлі протягом 3-х років. Рішення Складемо функціональну модель процесу (рис.7.3).
Рис.7.3 Модель процесу з вкладенням коштів у розвиток виробництва Перший крок. Знаючи початкове значення К1, одержуємо для К2:
К2 =
Враховуючи x2=К1 – х1 запишемо:
К2 = = K2 буде максимальним при х1 =K1
Таким чином, стратегія управління на 1-му кроці: x1=K1; x2=0. При
α1 =0,4, α2 =0,42; β1 =0,7; β2 =0,5:
Величина капіталовкладень на початок другого року K2=1,1K1. Другий крок. Аналізується аналогічно першому: К2 = = = max[ 0.08x1 + 1.02K2 ]=1,1 K2= 1,12 K1 при х1 =К1 і т.д.. Очевидно, що можливі варіанти закупівлі устаткування різного типу на кожен етап розвитку. У цьому випадку уточнюється значення αi і βi на кожному кроці. Можливо також поєднання різних схем використання коштів. Пропонуємо читачам самим вирішити задачу за умови, що на 1-му етапі весь прибуток вкладається в придбання устаткування, а на наступному повністю відраховується як дивіденд від діяльності підприємства Необхідно максимізувати прибуток за останні 2 роки.
Метод Монте-Карло Більшість процесів, що характерні для транспортних систем, значною мірою відбуваються під впливом випадкових факторів, які не підлягають контролю з боку осіб, відповідальних за прийняття і реалізацію рішень у контексті забезпечення оптимального функціонування систем. Проте з позицій системного аналізу врахування невизначеностей є обов'язковим елементом процедури вироблення планово-управлінських рішень. Задача полягає в тому, щоб якомога повніше врахувати вплив неконтрольованих випадкових факторів і зробити в таких умовах аргументований висновок щодо можливих напрямків розвитку системи та оптимальної стратегії нею. Такі задачі розв'язують за допомогою методу Монте-Карло (методу статистичних випробувань). Метод Монте-Карло являє собою сукупність формальних процедур, засобами яких відтворюються на ЕОМ будь-які випадкові фактори (випадкові події, випадкові величини з довільним розподілом, випадкові вектори тощо). Зауважимо, що «розігрування» вибірок за методом Монте-Карло є основним принципом імітаційного моделювання систем зі стохастичними (випадковими, імовірними) елементами. Зародження методу Монте-Карло пов'язане з дослідженнями фонНеймана та Улама наприкінці 40-х років, коли вони запровадили термін «метод Монте-Карло» і застосували цей метод до розв'язування деяких задач екранування ядерних випромінювань. Згаданий математичний метод був відомий давно, проте пережив своє друге народження, коли знайшов у Лос-Аламосі (США) застосування в закритих роботах з ядерної техніки, виконуваних під кодовою назвою «Монте-Карло». Результати були настільки успішними, що цей метод швидко поширився і в інших галузях науки і техніки. Для багатьох фахівців термін «метод Монте-Карло» є синонімом терміна «імітаційне моделювання». І хоча вибірковий метод Монте-Карло є найбільш корисним при моделюванні стохастичних ситуацій, він придатний також і для розв'язання деяких цілком детермінованих задач, що не мають аналітичних розв'язків.
Одним з найбільш поширеним прикладом застосування методу Монте- Рис.9.1 Визначення площі методом Монте-Карло Карло є визначення площі чи об'єму геометричних фігур, що не мають аналітичного виразу оточуючих фігуру границь. Розглянемо простий випадок. Нехай потрібно визначити площу фігури довільної форми, що не має аналітичного виразу (див. рис.9.1). Якщо на площі прямокутника (a x b) генерувати N точок з випадковими координатами у і х, що підкоряються рівномірному закону розподілу ймовірностей, і підраховувати кількість точок, як належать саме фігурі (n), то при великій кількості точок N можна стверджувати, що площа цієї фігури може бути визначена як: Рис.9.1 Визначення площі методом Монте-Карло
Очевидно, що такий спосіб визначення площі не потребує знання аналітичного виразу границь фігури. Головним при цьому є лише необхідність генерування послідовності N випадкових чисел, які підкоряються рівномірному закону розподілу ймовірності їх появи. Алгоритм аналізу кожної пари координат (уi і хi) є при цьому дуже простим: чи належить цяточка фігурі чи ні. Очевидно також, що точність визначення S цілком залежить від кількості генерованих точок N В теорії методу статистичних випробувань приводиться, що похибка результату визначається як Не менш важливим є правильний вибір закону розподілу ймовірностей появи певних чисел у випадкової послідовності. Наприклад, якщо в розглянутому раніше випадку при генеруванні випадкової послідовності координат точок не з рівномірним, а з нормальним законом розподілу їх відхилень від центру прямокутника, відношення n/N являє собою вже характеристику точності попадання у центр прямокутника, а аж ніяк не визначатиме площу фігури. Відмітимо, що саме необхідність генерування випадкової послідовності чисел з заданим законом їх розподілу, який відповідає реальним процесам, що протікають у реальній системі, є основною задачею імітаційного моделювання, а точність генерування заданого закону розподілу випадкових величин у значний мірі обумовлює точність результатів імітаційного моделювання. Види випадкових потоків При розгляді випадкових процесів, які протікають в системах з дискретними станами і безперервним часом, часто доводиться стикатися з так званими «потоками подій».
|
|||||||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 114; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.23.123 (0.243 с.) |
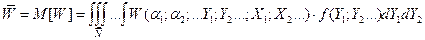 (1.3)
(1.3) ,
,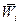 (і =
(і =  )- для критеріїв що максимізуються;
)- для критеріїв що максимізуються; )- для критеріїв, що мінімізуються,
)- для критеріїв, що мінімізуються, (об'єм перевезень не повинен бути менше за
(об'єм перевезень не повинен бути менше за 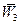 (собівартість перевезень не повинна перевищувати
(собівартість перевезень не повинна перевищувати 








 ,m – число етапів). Складніше буде с вибором управлінь (капіталовкладень в к-е підприємство на кожному і-му етапі xik).
,m – число етапів). Складніше буде с вибором управлінь (капіталовкладень в к-е підприємство на кожному і-му етапі xik).

 α1= 0,4; для 2-го типу α2 =0,42. Наприкінці звітного періоду використане устаткування реалізується за ціною 0,7 і 0,6 первісної вартості (коефіцієнти амортизації відповідно β1=0,7 і β2=0,6). Отримані від продажу кошти, а також отриманий прибуток знову вкладаються в придбання устаткування 1-го і 2-го типів.
α1= 0,4; для 2-го типу α2 =0,42. Наприкінці звітного періоду використане устаткування реалізується за ціною 0,7 і 0,6 первісної вартості (коефіцієнти амортизації відповідно β1=0,7 і β2=0,6). Отримані від продажу кошти, а також отриманий прибуток знову вкладаються в придбання устаткування 1-го і 2-го типів.
 [ α1х1 + α 2х2 + β1x1 + β 2x2 ]
[ α1х1 + α 2х2 + β1x1 + β 2x2 ] [ α1х1 + α2(k1 –х1) + β1x1 +β2 (К1 –х1)] =
[ α1х1 + α2(k1 –х1) + β1x1 +β2 (К1 –х1)] = [ α1х1 + α 2х2 + β1x1 + β 2x2 ] =
[ α1х1 + α 2х2 + β1x1 + β 2x2 ] = [ (α1 – α2 + β1 – β2 )x1 + (α 2 + β2)K2 ]=
[ (α1 – α2 + β1 – β2 )x1 + (α 2 + β2)K2 ]=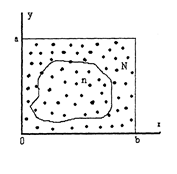

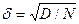 , де D – певна константа. Очевидно, що збільшення точності результату потребує збільшення кількості генерованих випадкових чисел у 100 разів. Саме необхідність генерування значної кількості випадкових чисел і є суттєвим недоліком цього методу. Вважається, що 90% задачі імітаційного моделювання систем приходиться саме на генерування випадкової послідовності чисел з заданим розподілом ймовірності і тільки 10% - на моделювання алгоритму функціонування системи.
, де D – певна константа. Очевидно, що збільшення точності результату потребує збільшення кількості генерованих випадкових чисел у 100 разів. Саме необхідність генерування значної кількості випадкових чисел і є суттєвим недоліком цього методу. Вважається, що 90% задачі імітаційного моделювання систем приходиться саме на генерування випадкової послідовності чисел з заданим розподілом ймовірності і тільки 10% - на моделювання алгоритму функціонування системи.


