
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розподіл напруження під час розтягуСодержание книги
Поиск на нашем сайте
Якщо розглядати балку як систему елементарних ниток, то можна передбачити, що вони подовжуються, і тим більше, чим більшим буде навантаження. Причому подовження всіх частинок буде однакове. Отже, матеріал в будь-якій точці поперечного перерізу однаково деформується. В такому випадку внутрішні сили пружності у всіх точках перерізу рівні. Мал.2.7. Розтяг бруса При рівномірному розподілі внутрішніх сил на площині перерізу, величину нормальних діючих напружень можна визначити, з відношення рівнодіючої внутрішніх сил
Залежність між напруженням та відносним подовженням В певних межах напруження розтягу Відносне подовження визначається за формулою:
Ця залежність була вперше досліджена англійським вченим Гуком. В його честь вона отримала назву - закон Гука. Фізична суть коефіцієнта пропорційності можна встановити, з припущення, що Тому можна сказати, що Е - таке напруження розтягу, яке виникає в матеріалі, при умові, якщо балка збільшує свою довжину на величину, яка рівна початковій довжині. Слід відмітити, що майже всі матеріали руйнуються значно раніше, ніж досягають величини Е, але величина такого напруження характеризує дійсні властивості матеріалу, його спроможність опиратися пружній деформації розтягу. Коефіцієнт пропорційності називають модулем пружності під час розтягу (модуль повздовжньої пружності). Величина Е для різних матеріалів різна. Наприклад, для сталі Е»2×1011 Па. Для практичних розрахунків зручніше використовувати інше математичне написання закону Гука. Під час дослідження розтягу воно дозволяє визначити величину абсолютної деформації балки під навантаженням.
Отже, абсолютне подовження, якого зазнала балка, прямопропорційне повздовжній силі і довжині балки та зворотно пропорційне площі поперечного перерізу і модулю пружності. Стиск, зім’яття Розглядаючи стиск деталі, ми можемо виявити, що сили, як у випадку розтягу, діють вздовж однієї осі. Відмінністю цього випадку навантаження є спрямованість сил. Вони направлені назустріч одна одній. Під час стиску матеріал у всіх точках поперечного перерізу піддається однаковим деформаціям. Внутрішні сили пружності розподіляються по перерізу, як і під час розтягу, рівномірно. Отже, величина дійсних напружень під час стиску може бути визначена за тією ж формулою:
де
Для дослідження явища стиску повною мірою можна застосувати закон Гука. Його математичне вираження аналогічне розглянутого під час розтягу. Особливістю деформації стиску є той факт, що вона може супроводжуватися деформацією зім’яття. Зім’яття виникає на опорній поверхні а-b (мал.2.9) контактуючих тіл, якщо одне з них тисне на інше. Саме в цьому і полягає основна відмінність зім’яття від стискування: стиск відбувається на внутрішніх поверхнях матеріалу, а зім’яття - на зовнішній поверхні. Під час зім’яття виникають нормальні напруження, які рівні у всіх точках опорної поверхні. Тому величина дійсних напружень зім’яття визначається за формулою:
де
|
|||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 447; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.137 (7.563 с.) |

 Деформація розтягу виникає у випадку, коли зовнішні сили спрямовані вздовж осі балки в протилежні сторони (мал.2.7).
Деформація розтягу виникає у випадку, коли зовнішні сили спрямовані вздовж осі балки в протилежні сторони (мал.2.7). (повздовжня сила) до площини поперечного перерізу бруса
(повздовжня сила) до площини поперечного перерізу бруса  :
: .
. прямо пропорційне величині відносного подовження
прямо пропорційне величині відносного подовження  . Відносне подовження - це величина, яка визначається як відношення абсолютного подовження (приросту довжини)
. Відносне подовження - це величина, яка визначається як відношення абсолютного подовження (приросту довжини) 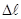 бруса до його початкової довжини
бруса до його початкової довжини 

 , то отримаємо формулу за допомогою якої визначають напруження розтягу
, то отримаємо формулу за допомогою якої визначають напруження розтягу  .
. =
=  . В такому випадку
. В такому випадку  .
. або
або 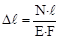
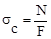

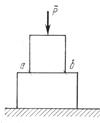 Мал..2.8. Стиск зразка Мал.2.9. Зім’яття зразка
Мал..2.8. Стиск зразка Мал.2.9. Зім’яття зразка
 ,
, - рівнодіюча внутрішніх сил, які прикладені до опорної поверхні контактуючих тіл;
- рівнодіюча внутрішніх сил, які прикладені до опорної поверхні контактуючих тіл;


