
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення небезпечного перерізу під час згину ⇐ ПредыдущаяСтр 8 из 8
Під час згинаючого навантаження створюється небезпечний переріз, в якому виникає найбільша загроза руйнуванню деталі. В цьому перерізі діє максимальний згинаючий момент. Важливим завданням є навчитися визначати положення небезпечного перерізу балки і згинального моменту в такому перерізі.
Ми вже проводили аналіз елементарного навантаження балки згинальним моментом. Тоді було визначено небезпечний переріз на основі логічного налізу схеми. Тепер проведемо більш глибоке дослідження. Для цього зобразимо балку схематично (мал.2.16). Для визначення внутрішніх силових факторів використаємо метод перерізів. Розглянемо рівновагу правої частини (мал.2.16,б). В перерізі 1 будуть діяти поперечна сила Аналогічні результати отримаємо і для інших випадків. Зрозуміло, що рухаючись по довжині балки, відбуватиметься наростання величини згинального моменту за лінійним законом. Це можна зобразити графічно: побудуємо так звану епюру моментів. Для цього виберемо масштаб для одиниці моменту, відкладемо від осьової лінії епюри (мал.2.16.,г) ординату, яка відповідає величині найбільшого моменту - Друга точка для побудови графіка відповідає вільному кінцю балки. В такому перерізі момент рівний нулю. З’єднавши точки а і б, отримаємо графік зміни згинального моменту по довжині балки, тобто епюру моментів. Проміжні між точками а і б ординати відповідають моментам у відповідних перерізах. Отже, для нашого випадку ми визначили, що небезпечний переріз в точці закріплення консолі, а згинаючий момент в цьому перерізі рівний Розглянемо більш складний випадок, коли балка двоопорна і навантажена силою, яка прикладена симетрично відносно опор (мал.2.17).
В цьому випадку метод перерізів застосувати одразу не можна. Виконавши умовний переріз балки, ми отримаємо частину, кінець якої закріплений. В такому випадку необхідно спочатку відкинути опори і замінити їх силами реакції (мал.2.17,б). Кожна реакція рівна половині діючої сили
Повздовжній згин Досліджуючи деформацію стиску, ми можемо помітити, що вона можлива у випадку дії на балку сил, які спрямовані по його повздовжній осі назустріч одна одній. При цьому поперечні розміри балки мало відрізняються від його розмірів. Якщо поперечні розміри балки будуть в багато раз меншими його довжини (такий брус називають стержень), то може виникнути другий напружений стан. Спочатку, коли сили невеликі, стержень дійсно піддається стискуванню, і його вісь буде залишатися прямолінійною. Однак, збільшуючи навантажувальну силу, можна досягти такої величини, при якій стержень починає виходити з стійкого положення, і його вісь стає криволінійною (мал.2.18,а). Зрозуміло, що працездатність деталі в такому випадку буде порушена. Деформація стержня, яка є наслідком втрати його стійкості під впливом стискуючих сил, називають повздовжнім згином. Сила, яка відповідає моменту переходу стержня з стійкого положення в нестійке, називається критичною силою, а напруження, яке відповідає цій критичній силі, - критичним напруженням. Практика показує, що це напруження менше звичайного граничного напруження, орієнтуючись на яке вибирають допустиме напруження під час стиснення. Щоб розрахунок на міцність одночасно гарантував стійкість, враховують залежність співвідношення довжини, поперечних розмірів стержня та спосіб закріплення його кінців. Наприклад стержень, закріплений, як показано на (мал.2.18,а) менш стійкий за стержень, зображений на (мал.2.18,б).
Складний опір До цього випадку ми розглянули елементарні випадки деформування: розтяг, стиск, зсув, кручення, поперечний та повздовжній згин. Але частина деталей сприймає одночасно декілька простих деформацій. Такі випадки називають складним опором. Найчастіше зустрічаються комбінації простих деформацій: розтяг (стиск) з згином; згин з крученням.
Мал.2.19. Складний опір (розтяг із згином).
Розтяг із згином. Якщо брус навантажений так, як зображено на мал.2.19,а, то це звичайна деформація розтягу. Якщо брус навантажити за схемою, зображеною на мал. 2.19,б, то це звичайна деформація поперечного згину. Коли ж навантаження буде таким, як показано на мал.2.19,в, то для визначення виду навантаження попередньо необхідно розкласти діючу силу на дві складові. З малюнку видно, що навантаження балки складається з двох попередньо розглянутих. Це означає, що деформуючі напруження будуть відповідати одночасно напруженням розтягу та напруженням згину. Одна складова Друга складова
В формулі
Нормальні напруження
Згин з крученням. Цей вид складної деформації зустрічається досить часто. Всі вали, безумовно, зазнають деформації кручення. Поряд з цим, під дією сил, які передають зубчаті колеса, паси, та інші деталі, вони зазнають деформації згину.
Проведемо аналіз кінематичної схеми, зображеної на мал.2.20,а. На ній зображено два вали, на яких зачеплені зубчаті колеса. Вони знаходяться в зачепленні одне з одним. До валу прикладений зовнішній обертовий момент Щоб визначити, яка деформація вала викликана силою В подібних випадках одночасної дії згинального та крутного напружень в небезпечних перерізах, алгебраїчно сумувати не можна. Адже вектори дотичних напружень кручення і нормальних напружень згину спрямовані не по одній прямій, а під прямим кутом. В таких випадках використовують спеціальні теорії міцності, які ми не розглядатимемо. Втомлюваність матеріалів Спостереженнями встановлено, що у випадку, коли на протязі довгого періоду навантаження, періодично змінюються від мінімального до максимального значення, руйнування деталі може відбутися навіть тоді, коли максимальні значення напруження не перевищують границі міцності і навіть границі текучості.
Навантаження, які змінюються за певним законом, називають циклічними. Напруження, викликані дією таких навантажень, також називаються циклічними. Сукупність послідовних значень, змінних напружень за один період, процесу їх зміни називають циклом напруження. Періодом циклу називається довжина одного циклу. Явище руйнування матеріалу деталі під дією періодично змінюваних (циклічних) навантажень називають втомлюваністю матеріалу. Встановлено, що структура матеріалу при циклічних навантаженнях не змінюється. Початок руйнування носить чисто місцевий характер. В зоні підвищених напружень, обумовлених конструктивними (виточки, шпонкові канавки…) або технологічними (раковини…) причинами, утворюється мікротріщина. Циклічні навантаження в зоні тріщини починають руйнувати кристали металу, і тріщина розростається в глибину деталі. Відбувається поступове накопичення пошкоджень, що супроводжується шліфовкою поверхні тріщин які розростаються. Це призводить до ослаблення перерізу і до миттєвого руйнування. Поверхня втомлюваного руйнування має дві характерні області. Перша – область поступового розростання тріщини; друга – зона миттєвого руйнування.
|
|||||||||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 522; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.42.208 (0.013 с.) |
 Мал.2.16. Згинаюче навантаження
Мал.2.16. Згинаюче навантаження
 і згинаючий момент
і згинаючий момент  . Розглянемо тепер переріз 2 (мал.2.16,в). В цьому перерізі буде діяти та ж сила
. Розглянемо тепер переріз 2 (мал.2.16,в). В цьому перерізі буде діяти та ж сила  .
. . При цьому приймемо позитивним вважати момент, якщо він прогинає балку до низу. За цією умовою момент, який діє на балку в нашому випадку, від’ємний.
. При цьому приймемо позитивним вважати момент, якщо він прогинає балку до низу. За цією умовою момент, який діє на балку в нашому випадку, від’ємний.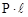 .
. Мал.2.17. Навантаження двоопорної балки.
Мал.2.17. Навантаження двоопорної балки.
 . Використовуючи метод перерізів, спочатку визначимо рівновагу відділених частин балки, яка розташована праворуч від середини прольоту. Якщо на кінці балки момент рівний нулю, то до середини він зростає до величини
. Використовуючи метод перерізів, спочатку визначимо рівновагу відділених частин балки, яка розташована праворуч від середини прольоту. Якщо на кінці балки момент рівний нулю, то до середини він зростає до величини 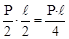 . Потім розглянемо рівновагу відокремленої частини балки, що розташована ліворуч від будь-якого перерізу. Результати будуть такими ж. Призначивши масштаб одиниці моменту і встановивши, що згинаючий момент додатній, відкладемо вгору по осі ординату
. Потім розглянемо рівновагу відокремленої частини балки, що розташована ліворуч від будь-якого перерізу. Результати будуть такими ж. Призначивши масштаб одиниці моменту і встановивши, що згинаючий момент додатній, відкладемо вгору по осі ординату  . Саме цю величину необхідно буде використати під час проектного та перевірного розрахунку балки на згин.
. Саме цю величину необхідно буде використати під час проектного та перевірного розрахунку балки на згин. Мал.2.18. Деформація повздовжнього згину
Мал.2.18. Деформація повздовжнього згину

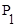 діючої сили
діючої сили  під час деформування розтягу, всі перерізи по довжині бруса, і всі точки в перерізі рівнобезпечні. Рівнодіюча внутрішніх сил
під час деформування розтягу, всі перерізи по довжині бруса, і всі точки в перерізі рівнобезпечні. Рівнодіюча внутрішніх сил  . Величина напруження
. Величина напруження 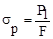 .
. діючої сили створює найнебезпечніший переріз в точці закріплення балки, а також в кожному перерізі найбільш небезпечні точки, які найбільш віддалено розташовані від нейтральної осі. Напруження в точках
діючої сили створює найнебезпечніший переріз в точці закріплення балки, а також в кожному перерізі найбільш небезпечні точки, які найбільш віддалено розташовані від нейтральної осі. Напруження в точках .
. - осьовий момент опору перерізу згину.
- осьовий момент опору перерізу згину. і
і 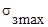 можна алгебраїчно скласти. Зробивши аналіз результатів наших досліджень, можна передбачити, що найбільш небезпечним є переріз, в якому закріплена балка. Величина напруження в ньому рівна:
можна алгебраїчно скласти. Зробивши аналіз результатів наших досліджень, можна передбачити, що найбільш небезпечним є переріз, в якому закріплена балка. Величина напруження в ньому рівна: .
. Мал..2.20. Складний опір (згин з крученням)
Мал..2.20. Складний опір (згин з крученням)
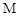 , під дією якого в зачепленні виникає сила, спрямована по дотичній до їх початкових кіл, - колова сила
, під дією якого в зачепленні виникає сила, спрямована по дотичній до їх початкових кіл, - колова сила 


