
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Количественная оценка информацииСодержание книги
Поиск на нашем сайте
Допустим, что есть М событий. Необходимо исследовать возможность реализации одного из М1 событий. После проведения исследований выяснили, что реализованы лишь М2 из М1 событий, но не ясно, какое именно из этих М2 событий реализовано в действительности. До исследования
После проведения исследования энтропия уменьшилась до значения, не превышающего
Количество полученной информации I определяется разностью между исходной и конечной энтропиями:
Количество информации равно убыли энтропии. Величина исчерпывающей энтропии соответствующей Н2 = 0 и равна исходной энтропии. Пример. Прибор со шкалой длинной L. Цена деления Δ равна цене деления шкалы. Допустим, что допустимая погрешность δ < Δ Исходя из заданной точности, прибор должен гарантировать Начальная энтропия
Энтропия после измерений
При δ > Δ, то Н2 = 0 Величина исчерпывающей информации равна исходной энтропии, на которую сориентировано работа измерительного комплекса. Воспользуемся двумя символами – 1 и 0. n = 2 если равновероятны два исхода события, тогда Н1 = 1(М1 = 2) и Н2 = 0 (М2 = 1). I =1. Получаемую информацию используют в качестве эталона (единицы информации). Это бит или двоичная единица информации. (Пример подбрасывания монеты). Отсюда следует, что максимальный объём информации, который может храниться на электронном триггере,равен одному биту. Производные от бита единицы информации: 1 байт = 8 бит; 1 кбайт = 210 байт; 1 Мбайт = 2*1020 байт Особой единицей является слово. Слово – это количество информации, обрабатываемой в данном управляющем устройстве за один цикл работы устройства. Величина слова кратна байту: 1 байт, 2 байта, 4 байта.
Кодирование информации Кодирование информации – это процесс формирования сообщений о событиях, составляющих управляемый техпроцесс. Два этапа кодирования: · Представление информации в дискретной форме (АЦП-ние);/ · Преобразование дискретных сигналов в наиболее подходящем для решения задач управления виде(преобразование кодов). Конкретный способ представления информации как системы соответствия между элементами сообщений и сигналами, их отображающими, называется кодом. Первоначально информация поступает от отдатчика или от ЗУ, ВЗУ и представляется в дискретной форме.
Рис.22.Преобразование информации Обозначения: ПК – преобразование кода; Д – датчик; ППр – первичный преобразователь; ГР – гальваническая развязка; УУ – устройство управления; ТО – технологический объект. По характеру взаимодействия с ППр сигналы датчиков подразделяются на дискретные и непрерывные (аналоговые). Если ППр выделяет в сигнале датчика только два (реже три) уровня, то такой сигнал считается дискретным. Пример: концевые выключатели. Если сигнал датчика дискретный, то ППр усиливает сигнал и осуществляет гальваническую развязку с УУ. Если сигнал непрерывный, ППр осуществляет АЦП-е. В этом случае ППр должен обеспечить достаточную разрешающую способность, соответствующую величине энтропии данного ТО. При использовании стрелочного прибора - это подходящая цена деления. РС – это шаг квантования по уровню. Ψ(x) - ступенчатая функция
Рис.24. Аналогово-цифровое преобразование Точность измерения зависит от скорости измерения.
Рис.25. Иллюстрация взаимосвязи точности и скорости измерения Частота отсчётов определяется шагом квантования по времени.
Приведенные формулы определяют требования к РС и быстродействию применяемых АЦП. Системы кодирования Различают десятичную и двоичную системы. Каждая система кодирования базируется на совокупности чётко определённых, специфических сигналов одной физической природы, называемых символами. Полная совокупность символов, на которой базируется система кодирования, составляет её алфавит. Конечная совокупность символов, входящих в принятую систему кодирования, называется кодовой комбинацией, словом или числом. Совокупность слов, правил их формирования и сочетания образуют разнообразные языки кодирования. В системах кодирования АСУ ТП применяются также совокупности символов как латинский и русский алфавиты, арабские цифры, знаки препинания, знаки математических операций и другие математические символы. Для представления чисел используют арифметические коды. Любое число может быть представлено:
где m, l – произвольные числа причём Произведение Q = am am-1 … a1 a0, a-1 … al. Пример: В АСУТП распространена двоичная система счисления. В двоичной системе для записи (арифметической) числовой информации применяется двоичный арифметический код n = 2. Используют две цифры 0 и 1. Рассмотрим запись двоичного числа, у которого m = 2, l = -2, a2 = 1, a1 = a0 = a-1 = 0, a-2 =1 Q = 1*22 + 0*21 + 0*20 + 0*2-1 + 0*2-2 = Опустив обозначение весов разрядов, получим запись данного числа в традиционном виде. Q = 100,01 Перевод целой части числа из десятичной в двоичную форму записи удобно производить методом деления. Число 25 25/2 = 12 (остаток 1) – младший разряд 12/2 = 6 (остаток 0) 6/2 = 3 (остаток 0) 3/2 = 1 (остаток 1) 1/2 = (остаток 1) – старший разряд. Q = 11001 = 1*24 + 1*23 + 0*22 + 0*21 + 1*20 Двоичные коды. Обработка информации процессором УВМ производится только в двоичных кодах. Два состояния (да - нет); (открыто - закрыто); (включено – выключено) и т.д. Обозначаются цифрой 0 или 1. Максимальное число возможных сообщений: M = nm
Сложность запоминающего устройства, пропорциональная произведению m*n, определяется из соотношения:
Продифференцировав по n и приравняв полученное производную к нулю, получим уравнение
Модуль №3
|
||||
|
Последнее изменение этой страницы: 2017-01-25; просмотров: 229; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.72.24 (0.008 с.) |




 точек измерения в пределах шкалы, фактически не имеет
точек измерения в пределах шкалы, фактически не имеет  .
.








 ;
;  - целое число, причём
- целое число, причём  ; n – целое число, основание системы исчисления (n >1).
; n – целое число, основание системы исчисления (n >1). называют разрядом закодированного числа, причём nj называют весом разряда, aj цифрой или цифровым значением разряда, а j – номером разряда. Если m = l, то закодированное число одноразрядное, состоит из одного разряда, а если все aj = 0, то Q = 0. Все разряды, у которых j < 0, входят в дробную часть закодированного числа, а остальные разряды составляют его целую часть. При записи чисел обычно опускают веса разрядов, а так же нули перед первой значащей цифрой целой части числа и после последней значащей цифры дробной части числа. Дробную часть от целой отделяют запятой или точкой. Запись числа приобретает вид:
называют разрядом закодированного числа, причём nj называют весом разряда, aj цифрой или цифровым значением разряда, а j – номером разряда. Если m = l, то закодированное число одноразрядное, состоит из одного разряда, а если все aj = 0, то Q = 0. Все разряды, у которых j < 0, входят в дробную часть закодированного числа, а остальные разряды составляют его целую часть. При записи чисел обычно опускают веса разрядов, а так же нули перед первой значащей цифрой целой части числа и после последней значащей цифры дробной части числа. Дробную часть от целой отделяют запятой или точкой. Запись числа приобретает вид: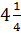

 .
.





