
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахункові схеми та основні елементи споруд
Як і в опорі матеріалів, в будівельній механіці вивчають не реальну споруду а її розрахункову схему. Її вибір – важливий етап розрахунку споруди, тому що це впливає як на об'єм розрахунку, так і на його точність. Розрахункова схема тісно пов’язана з допущеннями та передумовами, що лежать в основі подальших розрахунків. Для однієї і тієї ж споруди нерідко можна запропонувати різні розрахункові схеми, вибір яких залежить від методу та необхідної точності розрахунку. Розрахункова схема – це спрощене, ідеалізоване зображення дійсної споруди. Розрахунок споруд починають з вибору розрахункової схеми. При цьому: -ідеалізують опорні та вузлові з’єднання (або ідеальний шарнір, або абсолютно жорсткий вузол); -стержні споруди показують їх осями; -перевіряють геометричну незмінність системи (переміщення можливі тільки в результаті деформацій); -виключають непрацюючі стержні, тобто ті, які не навантажені і не потрібні для забезпечення стійкості споруди; -ідеалізують навантаження на споруду. При аналізі розрахункових схем споруд важливе значення мають поняття: диск, кінематична в’язь, ступінь вільності, ступінь статичної невизначеності, геометрична незмінність та ін. На даному етапі слід також усвідомити, що шарнір, який з’єднує не два, а n дисків (стержнів), еквівалентний (n-1) простим шарнірам. Основними елементами споруд є стійки та ригелі. У випадку з’єднання їх не жорстко – на розрахунковій схемі ставиться шарнір. Шарнірне з’єднання – з’єднання, в якому усунуто хоча б одну в’язь. У курсі будівельної механіки розглядається розрахунок геометрично незмінних систем (споруд), тобто таких, переміщення окремих точок яких можливі тільки в результаті деформації систем. Нерухомість таких систем (їхня геометрична незмінюваність) відносно землі забезпечується опорними зв'язками (опорами). В опорах виникають реакції, що разом із заданими навантаженнями встановлюють урівноважену систему зовнішніх сил, що діють на споруду. Розглянемо різні типи опор плоских систем. Перший тип опори представлений на рис. 1.1. Він складається з двох балансирів — верхнього 1 і нижнього 3, між якими прокладений валик 2, що грає роль циліндричного шарніра (надалі при розрахунку плоских систем «циліндричний шарнір» будемо називати «шарніром»). Завдяки цьому валику верхній балансир може повертатися щодо нижнього. Крім того, він може (разом з нижнім балансиром, що спирається на катки 4) переміщатися по опорній площині, яка називається опорною подушкою 5.
Розглянута опора має дві ступені вільності. Тертям, що виникає в опорі, прийнято при розрахунку нехтувати, а тому реакцією такої опори є сила, що проходить через центр шарніра перпендикулярно до напрямку можливого переміщення катків, тобто верхньої площини опорної подушки. Ця сила визначається одним параметром — її величиною. Розглянута опора називається циліндрично рухомою, або шарнірно рухомою. Схематично її зображують у вигляді одного стержня з двома ідеальними (без тертя) шарнірами на кінцях (рис. 1.2).Стержень, що схематично зображує шарнірно рухому опору, умовно приймається нескінченно довгим; верхня точка такого стержня може переміщуватися тільки по прямій лінії (пряма є коло нескінченно великого радіуса), перпендикулярної до його осі, що цілком відповідає тим умовам, у яких знаходиться дійсна шарнірно рухома опора. Власні деформації опори при розрахунках не враховуються, тобто опорний стержень умовно вважається, нескінченно твердим.
Третім типом опори є защімлення (рис. 1.5), ступінь вільності якої дорівнює нулю. Реакція такої опори визначається трьома параметрами: величиною і напрямком сили, що проходить через довільну точку, та моментом відносно цієї точки. Цю реакцію можна представити як поєднання реактивного моменту в защімленні (опорному перерізі) із реакцією шарнірно нерухомої опори. Схематично опора третього типу може бути представлена трьома стержнями (рис. 1.6); для того щоб защемлення можна було вважати абсолютно твердим, відстань lо повинна бути дуже малою або брус на ділянці довжиною lо треба розглядати як нескінченно твердий. Відзначимо, що число стержнів у схематичному, зображенні будь-якої опори завжди дорівнює, числу параметрів, що визначають повну реакцію цієї опори.
Кінематичний аналіз споруд
Інженерна споруда, яка складається з окремих елементів, може сприймати навантаження тільки в тому випадку, коли вона постійно зберігає геометричну форму і положення, які задані їй при зведенні (бути нерухомою і незмінною ). Змінність системи – її властивість змінювати свою геометричну форму без деформації матеріалу елементів споуди. Змінні системи не в змозі врівноважити зовнішні сили і під дією прикладених навантажень приходять в рух, міняють свою форму
Природно, що такі системи не можна використовувати як споруди. Геометрично незмінна система – це така система, форма якої не може мінятися без деформації матеріалу її елементів. Елементи споруди, незмінність яких очевидна або доведена, називаються дисками (стержень, земля). Рухоме з’єднання двох дисків, яке обмежує взаємне їх переміщення, називається кінематичною в’яззю. Якщо замінити жорсткі вузли системи, що складається з трьох стержнів (зображеної на рис. 1.7, а), циліндричними шарнірами, то система залишиться геометрично незмінною (рис. 1.7, б), тобто такою, зміна форми якої можливо лише в зв'язку з деформаціями її елементів. Якщо ж замінити жорсткі вузли шарнірами в системі, що складається з чотирьох стержнів (зображеної на рис. 1.8, а), то вийде система геометрично змінна (рис. 1.8, б), тобто така, форма якої може мінятися без деформації її елементів. Найпростішою геометрично незмінною шарнірною системою (фермою) є система з трьох стержнів (дисків), з'єднаних шарнірами в трикутник (рис. 1.7, б). Якщо замінити жорсткі вузли системи, що складається з трьох стержнів (зображеної на рис. 1.7, а), циліндричними шарнірами, то система залишиться геометрично незмінною (рис. 1.7, б), тобто такою, зміна форми якої можливо лише в зв'язку з деформаціями її елементів. Якщо ж замінити жорсткі вузли шарнірами в системі, що складається з чотирьох стержнів (зображеної на рис. 1.8, а), то вийде система геометрично змінна (рис. 1.8, б), тобто така, форма якої може мінятися без деформації її елементів. Найпростішою геометрично незмінною шарнірною системою (фермою) є система з трьох стержнів (дисків), з'єднаних шарнірами в трикутник (рис. 1.7, б). Положення точки на площині визначається двома параметрами (рис. 1.9.а), тобто ступінь вільності точки на площині дорівнює двом. Щоб визначити положення відрізка на площині, потрібно знати три незалежних параметри (рис. 1.9.6). Якщо на довільній плоскій фігурі провести відрізок, (рис. 1.9.в) то стає очевидним, що і для визначення положення плоскої фігури на площині потрібно знати три незалежних параметри; з цього випливає, що ступінь вільності плоскої фігури на площині дорівнює трьом. Ступінь вільності можна обмежити різними пристроями (в'язями), які зменшують кількість незалежних параметрів руху тіла чи системи тіл.
Рис.1.9 Пристрій, який зменшує ступінь вільності на одиницю, еквівалентний одній кінематичній в'язі. Таким пристроєм є вже розглянута нами шарнірно-рухома опора. Рухомий шарнір еквівалентний одній кінематичній в'язі, тому що не перешкоджає ні взаємному повороту елементів, ні просторовому їх переміщенню.
Рис.1.10 Нерухомий опорний шарнір накладає на тіло дві в'язі, чим і пояснюється символічне зображення двома опорними стержнями шарнірно-нерухомої опори. Шарнір, який з'єднує два плоских тіла,наприклад два стержні, характеризується як пристрій з двома кінематичними в'язями. Для наочного тлумачення сказаного вище стержні 1 і 2 (рис. 1.10. а) з'єднаємо шарніром С (рис. 1.10. б). Якщо для визначення положення першої системи (а) потрібно знати шість незалежних геометричних параметрів (по три на кожний стержень), то для другої - чотири. При відомому розташуванні в системі ХОУ першого стержня - положення другого в довільний момент часу визначається кутом ер. Ступінь вільності за рахунок шарнірного з'єднання двох стержнів зменшилась з шести до чотирьох.
Рис.1.11 С =. Якщо длявизначення ступеня вільності системи, зображеної на (рис. 1.11. а), умовно роз'єднати шарнірні з'єднання, то для визначення положення трьох стержнів в системі ХОУ ( рис. 1.11. б) потрібно знати дев'ять геометричних параметрів. Кожен шарнір накладає дві кінематичні в'язі. За рахунок трьох з'єднувальних шарнірів накладено шість кінематичних в'язей. Ступінь вільності заданої системи дорівнює трьом. З іншої сторони, задана в нашому прикладі система являє собою трикутник,форма якого, як відомо, не може бути змінена без зміни довжин сторін. Цей трикутник можна розглядати як плоске тіло, ступінь вільності якого і дорівнює трьом. Ступінь вільності системи, утвореної чотирма стержнями, зв'язаними шарнірними з'єднаннями в прямокутник (рис. 11.а), дорівнює чотирьом.
Рис.1.12
Про властивість шарнірно-рухомої опори накладати одну кінематичну в'язь, вже було сказано. Якщо два плоских тіла (два стержні) з'єднати стержнем, на кінцях якого ідеальні шарніри (рис. 1.12.6), то і в цьому випадку буде накладено одну кінематичну в'язь. На рис. 1.12.6 з'єднувальний стержень під номером три. Довести цю властивість пропонується самостійно.
Стержнева система - це сукупність певного числа стержнів (два основних розміри яких малі порівняно з третім), з'єднаних між собою відповідним чином в'язями. Ступінь вільності системи, складеної з дисків, з'єднаних між собою шарнірами, визначається наступним чином. Якщо число дисків позначити Д, а ступінь вільності кожного диска дорівнює трьом, то розміщені на площині диски будуть мати ступінь вільності рівний ЗД.. Враховуючи, що кожен простий шарнір, число яких позначимо Ш, зменшує ступінь вільності на два, а кожен опорний стержень(опорна в'язь, число яких позначимо С 0) - на одиницю, то загальнаступінь вільності (W) стержневої системи визначиться за формулою: W=ЗД-2Ш-С0. (1) Можливі три якісно різні результати: 1. W > 0 – система немає достатньої кількості в’язей -геометрично змінна, має рух; 2. W = 0 – система має достатнью кількость в’язей, необхідну для забезпечення геометричної незмінності і нерухомості; 1. W = 0 – система незмінна, має зайву кількость в’язей, число яких n = - W. Для правильного застосування формули (1) потрібно розрізняти шарніри прості – з’єднують два диски, і кратні - з’єднують більше двох дисків. Число простих шарнірів Ш в кратному визначається числом з’єднаних в ньому дисків (стержнів) Д зменшеним на одиницю – Ш=2Д-1.
Миттєво змінювана система – це система з’єднання дисків (стержнів), які допускають без деформації матеріалу безкінечно малі переміщення дисків (стержнів) в перший момент прикладення навантаження, після чого система стає незмінною. В миттєво змінюваних системах при дії довільного навантаження виникають безкінечно великі зусилля або невизначеної величини.
Розглянемо систему з двох стержнів (рис. 1.14), що лежать на одній прямій і з'єднують вузол С з двома нерухомими точками А и В. Якщо роз'єднати стержні АС і ВC у точці C, то кінець C стержня АС переміститься по колу m - m, а кінець C стержня ВC - по колу n - n. Ці кола в точці C мають загальну дотичну. Отже, якщо точка C одного зі стержнів одержить досить мале переміщення по перпендикуляру до АВ, то інший стержень не зможе перешкодити цьому переміщенню. Таким чином, розглянута система є геометрично змінюваною, тому що її форма може мінятися при незмінній довжині стержнів, тобто при відсутності деформацій її елементів. Система з двома стержнями, що лежать на одній прямій (див. рис. 1.14), надалі будемо називати миттєво змінною тому, що вона в наступну мить після малого переміщення точки C по перпендикулярі до прямої АВ перетворюється в незмінну систему.
Інша картина виходить, якщо стержні АС і ВС не лежать на одній прямій (рис. 1.15); у цьому випадку кола m–m і n–n не мають загальної дотичної, а тому навіть досить мале переміщення вузла C неможливо без деформації стержнів. Таким чином, всякий новий вузол, що додається в процесі утворення геометрично незмінної системи, може бути приєднаний за допомогою двох стержнів, осі яких не повинні лежати на одній прямій. Отже, системи, отримані із шарнірного трикутника шляхом послідовного приєднання вузлів, причому кожного двома стержнями, що не лежать на одній прямій, геометрично незмінні, тобто геометрична структура їх незмінна. Такі системи (або ферми) називають найпростішими, на відміну від складних, які утворюються, зазвичай, в результаті видозміни найпростіших. Перейдемо тепер до питання про приєднання геометрично незмінної системи до землі за допомогою опор.
Найчастіше споруда (диск) опирається на дві шарнірні опори, одна з яких нерухома, інша рухома (рис. 1.16, а). Такий зв'язок споруди з землею забезпечує йому геометричну незмінюваність. Не обов'язково, щоб два з трьох опорних стержнів з”єднувалися одним загальним шарніром; стержні геометрично незмінної системи можуть і не мати загальних шарнірів (рис. 1.16, б). Якщо всі опорні стержні розміщенні так, що їхні напрямки перетинаються в одній точці О (рис. 1.17, а), то ця точка є миттєвим центром, навколо якого система може робити безкінечно мале обертальне переміщення. Після такого переміщення всі опорні стержні вже не будуть перетинатися в одній точці і тому подальші переміщення будуть неможливі без деформації стержнів. Система, прикріплена до землі подібним чином, має миттєву змінність; тому таке розташування стержнів неприпустимо. Таким чином, прикріплення системи до землі за допомогою трьох стержнів можливо лише в тому випадку, коли осі цих стержнів не перетинаються в одній точці і не паралельні один одному. Поширюючи це положення на випадок взаємного з'єднання двох будь-яких геометрично незмінних систем (дисків), можна сформулювати наступне правило: два диски утворять геометрично незмінну систему, якщо вони зв'язані між собою за допомогою трьох стержнів, осі яких не перетинаються в одній точці і не паралельні між собою (спосіб Шухова). Якщо в точці перетинання напрямків будь-яких двох з цих трьох стержнів поставити шарнір і з'єднати його з диском, то система не стане геометрично змінною, але це дасть можливість розглядати її як систему, що складається з двох дисків І і ІІ, зв'язаних один з одним одним загальним шарніром А і стержнем В (рис. 1.17, б). Отже, до диска можна геометрично незмінно приєднати інший диск за допомогою загального для обох дисків шарніра і стержня, напрямок якого не повинен проходити через цей шарнір (спосіб Полонсо).
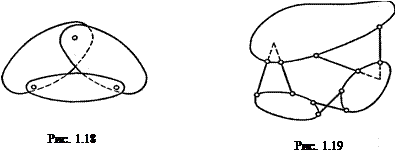
Зчленування трьох дисків в одну загальну геометрично незмінну систему можна здійснити, з'єднавши їх у трикутник за допомогою трьох шарнірів, не розташованих на одній прямій (рис. 1.18), або за допомогою шести стержнів, як це показано на рис. 1.19 тому, що кожний шарнір може бути замінений двома стержнями, що перетинаються в його центрі.
Отже, три диски, з'єднані за допомогою шести стержнів так, що між кожною парою дисків установлено по два стержні, точки перетину яких не лежать на одній прямій, утворюють нову геометрично незмінну систему. Загальний висновок незмінності стержневих систем: якщо система може бути зведена до шарнірного трикутника, то вона геометрично незмінна Порядок проведення кінематичного аналізу споруд: - вибір розрахункової схеми споруди; -визначення числа ступенів вільності системи; - виділення незмінних частин споруди – дисків; -.проведення аналізу з’єднань дисків між собою. Тема 2. Розрахунок балок та простих рам на нерухоме навантаження
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 651; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.17.45 (0.028 с.) |

 Другий тип опори (рис. 1.3) відрізняється від першого тим, що нижній балансир 3 закріплений і не може переміщуватися. Така опора має одну ступінь вільності і називається циліндрично нерухомою, або шарнірно нерухомою. Реакція її - це сила, що проходить через центр шарніра. Ця сила може мати будь-який напрямок і визначається, отже, двома параметрами - величиною і напрямком (або, що те ж саме, величинами двох складових її сил, наприклад: вертикальної і горизонтальної).Схематично опора другого типу зображується за допомогою двох стержнів з ідеальними шарнірами на кінцях; верхній шарнір є загальним для обох стержнів (рис. 1.4). Така схема визначає точку прикладання опорної реакції (центр верхнього шарніра), залишаючи її напрямок невідомим. Напрямки стержнів на схемі шарнірно нерухомої опори можуть бути обрані цілком довільно, тому що силу (реакцію) можна розкласти на два будь-яких напрямки.
Другий тип опори (рис. 1.3) відрізняється від першого тим, що нижній балансир 3 закріплений і не може переміщуватися. Така опора має одну ступінь вільності і називається циліндрично нерухомою, або шарнірно нерухомою. Реакція її - це сила, що проходить через центр шарніра. Ця сила може мати будь-який напрямок і визначається, отже, двома параметрами - величиною і напрямком (або, що те ж саме, величинами двох складових її сил, наприклад: вертикальної і горизонтальної).Схематично опора другого типу зображується за допомогою двох стержнів з ідеальними шарнірами на кінцях; верхній шарнір є загальним для обох стержнів (рис. 1.4). Така схема визначає точку прикладання опорної реакції (центр верхнього шарніра), залишаючи її напрямок невідомим. Напрямки стержнів на схемі шарнірно нерухомої опори можуть бути обрані цілком довільно, тому що силу (реакцію) можна розкласти на два будь-яких напрямки.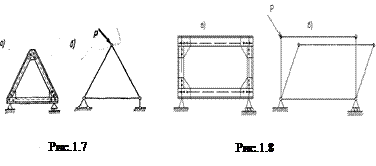



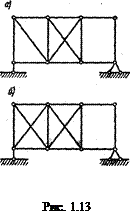 Співвідношення W=ЗД-2Ш-С є необхідною, але ще недостатньою умовою незмінюваності споруд. Так ферма, показана на рис. 1.13, а, геометрично змінювана, хоча ступінь вільності W=ЗД-2Ш-С = 3*13-2*18-3=0;; на рис. 1.13., б зображена змінювана ферма, для якої W=ЗД-2Ш-С =. С =. 3*14-2*20-3=-1. Змінюваність цих ферм пояснюється тим, що праві їхні частини - шарнірні чотирикутники. Отже стержневі системи, що задовільняють умову W=ЗД-2Ш-С, можуть бути миттєво змінюваними.
Співвідношення W=ЗД-2Ш-С є необхідною, але ще недостатньою умовою незмінюваності споруд. Так ферма, показана на рис. 1.13, а, геометрично змінювана, хоча ступінь вільності W=ЗД-2Ш-С = 3*13-2*18-3=0;; на рис. 1.13., б зображена змінювана ферма, для якої W=ЗД-2Ш-С =. С =. 3*14-2*20-3=-1. Змінюваність цих ферм пояснюється тим, що праві їхні частини - шарнірні чотирикутники. Отже стержневі системи, що задовільняють умову W=ЗД-2Ш-С, можуть бути миттєво змінюваними.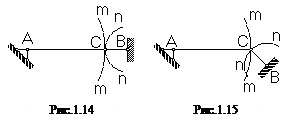

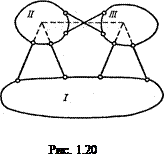 Система, зображена на рис. 1.20, миттєво змінювана тому, що точки перетину осей стержнів, що зв'язують кожну пару дисків, лежать на одній прямій.
Система, зображена на рис. 1.20, миттєво змінювана тому, що точки перетину осей стержнів, що зв'язують кожну пару дисків, лежать на одній прямій.


