
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование совместных зависимых событийСодержание книги
Поиск на нашем сайте
Пусть события A и B имеют вероятности свершения Покажем способ моделирования совместных зависимых событий на примере. Пример 3.9. При испытании нового автомата определены вероятности горизонтального и вертикального отклонений пробоин от точки прицеливания Вероятность отклонения пробоин по высоте относительно тех, которые уложились в пределы допустимого бокового отклонения, равна:
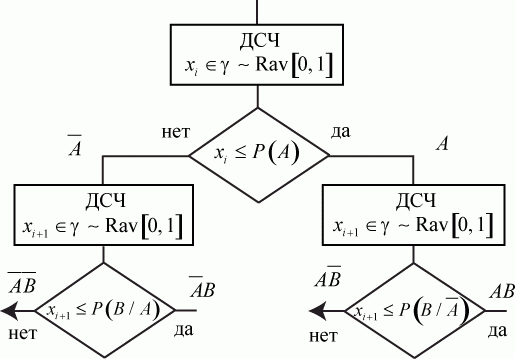
Соответствующий фрагмент модели приведен на рис. 3.18.
Пример 3.10. В ремонтное подразделение поступают вышедшие из строя средства связи (СС). В каждом СС могут быть неисправными в любом сочетании блоки A, B, C. Вероятности выхода из строя блоков Построить алгоритм имитационной модели с целью определения абсолютного и относительного количества отремонтированных СС с неисправными блоками A, B, C и A, B из общего количества R поступивших в ремонт СС. Решение Для имитации неисправных блоков СС и имитации наличия исправных блоков в ремонтном подразделении воспользуемся способом определения по жребию. Для этого рассчитаем вероятности исходов и сведем их в табл. 3.5 и 3.6 соответственно.
Так как нужно определить абсолютное и относительное количества отремонтированных СС, поступивших с неисправными блоками A, B и A, B, C, то нет смысла рассчитывать вероятности для других сочетаний неисправных и исправных блоков. Алгоритм имитационной модели приведен на рис. 3.19. В алгоритме приняты следующие обозначения:
Согласно постановке задачи в блоках 3…7 по данным табл. 3.5 разыгрывается, с какими неисправными блоками поступает СС в ремонт. В результате розыгрыша определяется номер интервала (столбца табл. 3.5) и запоминается в переменной Аналогично в блоках 8…11 разыгрывается по данным табл. 3.6 наличие в ремонтном подразделении необходимых блоков для замены. Если такие блоки имеются, т. е. выполняется условие
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 192; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.112.15 (0.006 с.) |

 и
и 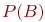 соответственно. Условная вероятность
соответственно. Условная вероятность 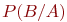 известна.
известна.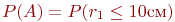 и
и 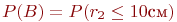 .
.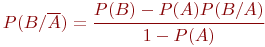
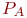 ,
, 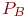 ,
, 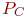 соответственно. Ремонт производится путем замены неисправных блоков исправными блоками. В момент поступления неисправного СС вероятности наличия исправных блоков
соответственно. Ремонт производится путем замены неисправных блоков исправными блоками. В момент поступления неисправного СС вероятности наличия исправных блоков 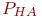 ,
,  ,
, 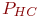 соответственно. При отсутствии хотя бы одного из исправных блоков A, B, C ремонт неисправного СС не производится.
соответственно. При отсутствии хотя бы одного из исправных блоков A, B, C ремонт неисправного СС не производится.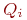



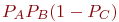
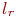

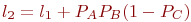


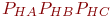
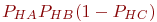

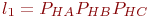
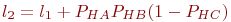
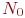 - заданное количество реализаций модели;
- заданное количество реализаций модели;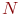 - счетчик количества реализаций модели;
- счетчик количества реализаций модели; 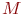 - счетчик числа отремонтированных СС за
- счетчик числа отремонтированных СС за 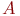 - абсолютное количество отремонтированных СС;
- абсолютное количество отремонтированных СС; - относительное количество отремонтированных СС.
- относительное количество отремонтированных СС.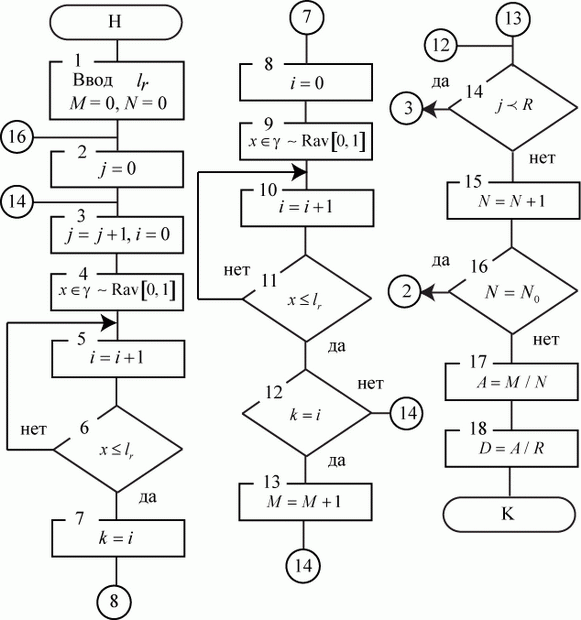
 .
.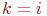 в блоке 12, в счетчик
в блоке 12, в счетчик 


