
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическое моделирование при решении детерминированных задачСодержание книги
Поиск на нашем сайте
Метод статистических испытаний может быть использован как численный метод решения математических задач. Именно в таком качестве он был применен в США в 1944 г. Джоном фон Нейманом при расчетах по созданию ядерного реактора. Применение метода рассмотрим на примере вычисления некоторого интеграла. Пример 3.4. Пусть Требуется вычислить Решение Представим функцию в координатах Имитируем координаты каждой точки значениями
Рассмотрим пару чисел Введем:
Число точек, попавших в границы
Чем больше будет элементарных площадей - точек, тем точнее будет вычислен интеграл. Приведенное решение примера справедливо для единичных областей существования функции и аргумента. Однако это несущественно, так как произвольные границы существования Известны статистические алгоритмы численного решения многократных интегралов. Пример 3.5. Найти оценку Решение Область интегрирования ограничена линиями
Площадь области интегрирования (прямоугольного треугольника)
в которой
а число случайных точек Результаты моделирования приведены в табл. 3.2. Из данных табл. 3.2 (верхние пять строк) видно, что с увеличением числа реализаций
В четырех нижних строках табл. 3.2 приведены результаты моделирования с другими начальными числами генераторов равномерно распределенных случайных чисел. Как видно, ошибка в оценке интеграла равна нулю уже при В заключение отметим, что имитационное (статистическое) моделирование целесообразно применять в случаях:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 154; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.195.8 (0.005 с.) |

 ,
,  . Полагаем, что функция
. Полагаем, что функция  такова, что интеграл относится к "неберущимся".
такова, что интеграл относится к "неберущимся". .
. как показано на рис. 3.7. Как известно, численное значение интеграла данного вида равно площади
как показано на рис. 3.7. Как известно, численное значение интеграла данного вида равно площади  . Площадь
. Площадь  состоит из множества элементарных площадок - точек. Количество точек в этой площади и будет численным значением искомого интеграла.
состоит из множества элементарных площадок - точек. Количество точек в этой площади и будет численным значением искомого интеграла. и
и 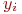 , принадлежащими равномерному распределению на участке
, принадлежащими равномерному распределению на участке  :
:

 . Вычислим
. Вычислим 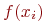 и сравним с
и сравним с  , то это означает, что точка
, то это означает, что точка  принадлежит площади
принадлежит площади  , то это означает, что точка
, то это означает, что точка 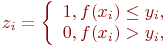
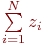 , где
, где 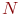 - общее число точек, попавших в единичную площадь существования функции и аргумента. Отсюда следует:
- общее число точек, попавших в единичную площадь существования функции и аргумента. Отсюда следует:
 заменой переменных можно свести к единичным границам.
заменой переменных можно свести к единичным границам. интеграла
интеграла  .
. ,
,  ,
,  , т. е. принадлежит единичному квадрату (рис. 3.8).
, т. е. принадлежит единичному квадрату (рис. 3.8).
 . Используем формулу
. Используем формулу
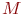 - число случайных точек
- число случайных точек  , принадлежащих области интегрирования. У этих точек
, принадлежащих области интегрирования. У этих точек  . Если данное условие выполняется, то вычисляется
. Если данное условие выполняется, то вычисляется
 :
:  .
. в определении оценки интеграла
в определении оценки интеграла  уменьшается и при
уменьшается и при  становится равной нулю.
становится равной нулю.


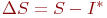
 реализаций модели.
реализаций модели.


