
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Классификация моделей и моделированияСодержание книги
Поиск на нашем сайте
Лекция: Введение Имитационное моделирование как необходимая часть инженерного образования сложилось в середине прошлого, двадцатого века. Воспринятое поначалу как своеобразный численный метод решения сложных задач, как "младший брат" аналитического моделирования, оно постепенно стало основным, подчас единственным методом при анализе и синтезе сложных систем и процессов. Общеизвестно, что правильно поставленный натурный эксперимент, то есть исследование свойств объекта на самом объекте, максимально информативен. Оказывается, что эксперимент с компьютерной имитационной моделью вполне конкурентоспособен с натурным. Не говоря о том, что натурный эксперимент в ряде случаев вообще невозможен или нецелесообразен, эксперимент с имитационной моделью может быть приемлемо информативен и выполнен значительно быстрее и дешевле натурного. Это и предопределило стремительное и повсеместное внедрение имитационного моделирования в научный и инженерный обиход. В популяризации имитационного моделирования заметную роль сыграли работы Р. Шеннона и Т. Д. Шрайбера. В свое время эти работы были широко известны в среде научных работников и инженеров. Большую положительную роль в распространении компьютерного имитационного моделирования у нас в стране сыграли работы по моделированию сложных систем на ЭВМ члена-корреспондента АН СССР Н. П. Бусленко и выдающегося математика академика АН СССР А. А. Самарского. Их работы в области математического моделирования и вычислительного эксперимента широко используются на практике. Огромный мировой опыт применения имитационного моделирования вызвал необходимость теоретического осмысления этого метода познания. Образовались центры в Москве, Санкт-Петербурге, Казани и др., объединяющие инженеров, научных сотрудников и преподавателей высшей школы, применяющих и пропагандирующих как само имитационное моделирование, так те или иные инструментальные средства. Регулярно проводятся общероссийские научно-практические конференции. Все чаще стали появляться публикации, посвященные общей теории имитационного моделирования. В частности, к таким можно отнести работы Окольнишникова В. В. и Н. Б. Кобелева. Курс имитационного моделирования под разными названиями: "Компьютерное моделирование", "Моделирование систем", "Моделирование" и т. п. является обязательным в учебных планах технических ВУЗов, в том числе и военных. Соответствующие знания включены в квалификационные характеристики выпускников. Настоящий курс представляет собой учебное пособие для изучения материала по этим дисциплинам. Содержание курса определено типовыми программами соответствующих специальностей и изложено в восьми лекциях. Первая лекция носит вводный характер. Разъясняются понятия моделирования и основных терминов. Классификация моделей и моделирования дается в самом общем виде. Подробная классификация не актуальна для настоящего пособия, главной целью которого является обучение практическим приемам имитационного моделирования и проведению компьютерных экспериментов с моделью. Заметим, что и общепринятой универсальной классификации нет, да и вряд ли она целесообразна. Этапы моделирования также рассматриваются в виде общего представления. Углубленное раскрытие содержания этапов демонстрируется в ходе курсового проектирования, предусмотренного тематическими планами вышеназванных дисциплин. Во второй лекции рассматриваются подходы к аналитическому моделированию дискретных процессов, обладающих свойством марковости. Как показывает практика, такие процессы присущи многим аспектам функционального и надежностного поведения систем - объектов профессионального предназначения выпускников учебных заведений соответствующих специальностей. Демонстрируемые в лекции аналитические модели противоборства, массового обслуживания и некоторые другие утилитарного значения не имеют; на этих примерах демонстрируются возможные подходы к построению аналитических моделей процессов в объектах разного назначения. Заметим, что для сравнительно несложных процессов, например, для ряда структур систем массового обслуживания, аналитические модели можно обнаружить в соответствующих справочниках. В основной части курса (лекции 3…8) излагаются обоснования и приемы имитационного моделирования дискретных процессов - моделирования поведения вероятностных систем, т. е. таких, на которые воздействуют различного рода случайности. Такие модели называются статистическими, поскольку искомые результаты получают посредством статистической обработки данных. В качестве основного инструментального средства в курсе рассматривается система моделирования GPSS World. Эта система распространена в нашей стране и не только; ей посвящены представительные научно-практические конференции и издания. Авторы имеют опыт применения и преподавания всех вариаций семейства GPSS, начиная с самой первой. И если версии GPSS-360, GPSS/PC, GPSS/H можно упрекнуть в некоторой ограниченности средств по сравнению, например, с Simpas, то последнюю на сегодняшний день версию GPSS World можно, по мнению инженерной общественности и авторов, считать вполне удовлетворяющей современным требованиям практиков. В учебном пособии нельзя, да и нецелесообразно отобразить все возможности GPSS World.
1. Лекция: Понятие модели и моделирования: Сам по себе процесс моделирования в полной мере не формализован, большая роль в этом принадлежит опыту инженера. Но, тем не менее, рассматриваемый в теме процесс создания модели в виде шести этапов может стать основой для начинающих и с накоплением опыта может быть индивидуализирован. Математическая модель, являясь абстрактным образом моделируемого объекта или процесса, не может быть его полным аналогом. Достаточно сходства в тех элементах, которые определяют цель исследования. Для качественной оценки сходства вводится понятие адекватности модели объекту и, в связи с этим, раскрываются понятия изоморфизма и изофункционализма. Формальных приемов, позволяющих автоматически, "бездумно", создавать адекватные математические модели, нет. Окончательное суждение об адекватности модели дает практика, то есть сопоставление модели с действующим объектом. И, тем не менее, усвоение всех последующих тем пособия позволит инженеру справляться с проблемой обеспечения адекватности моделей. Завершается тема изложением требований к моделям, которые были сформулированы Р. Шенноном на заре компьютерного моделирования тридцать лет назад в книге "Имитационное моделирование систем - искусство и наука". Актуальность этих требований сохраняется и в настоящее время. Общее определение модели Практика свидетельствует: самое лучшее средство для определения свойств объекта - натурный эксперимент, т. е. исследование свойств и поведения самого объекта в нужных условиях. Дело в том, что при проектировании невозможно учесть многие факторы, расчет ведется по усредненным справочным данным, используются новые, недостаточно проверенные элементы (прогресс нетерпелив!), меняются условия внешней среды и многое другое. Поэтому натурный эксперимент - необходимое звено исследования. Неточность расчетов компенсируется увеличением объема натурных экспериментов, созданием ряда опытных образцов и "доводкой" изделия до нужного состояния. Так поступали и поступают при создании, например, телевизора или радиостанции нового образца. Однако во многих случаях натурный эксперимент невозможен. Например, наиболее полную оценку новому виду вооружения и способам его применения может дать война. Но не будет ли это слишком поздно? Натурный эксперимент с новой конструкцией самолета может вызвать гибель экипажа. Натурное исследование нового лекарства опасно для жизни человека. Натурный эксперимент с элементами космических станций также может вызвать гибель людей. Время подготовки натурного эксперимента и проведение мероприятий по обеспечению безопасности часто значительно превосходят время самого эксперимента. Многие испытания, близкие к граничным условиям, могут протекать настолько бурно, что возможны аварии и разрушения части или всего объекта. Из сказанного следует, что натурный эксперимент необходим, но в то же время невозможен либо нецелесообразен. Выход из этого противоречия есть и называется он "моделирование". Моделирование - это замещение одного объекта другим с целью получения информации о важнейших свойствах объекта-оригинала. Отсюда следует. Моделирование -это, во-первых, процесс создания или отыскания в природе объекта, который в некотором смысле может заменить исследуемый объект. Этот промежуточный объект называется моделью. Модель может быть материальным объектом той же или иной природы по отношению к изучаемому объекту (оригиналу). Модель может быть мысленным объектом, воспроизводящим оригинал логическими построениями или математическими формулами и компьютерными программами. Моделирование, во-вторых, это испытание, исследование модели. То есть, моделирование связано с экспериментом, отличающимся от натурного тем, что в процесс познания включается "промежуточное звено" - модель. Следовательно, модель является одновременно средством эксперимента и объектом эксперимента, заменяющим изучаемый объект. Моделирование, в-третьих, это перенос полученных на модели сведений на оригинал или, иначе, приписывание свойств модели оригиналу. Чтобы такой перенос был оправдан, между моделью и оригиналом должно быть сходство, подобие. Подобие может быть физическим, геометрическим, структурным, функциональным и т. д. Степень подобия может быть разной - от тождества во всех аспектах до сходства только в главном. Очевидно, модели не должны воспроизводить полностью все стороны изучаемых объектов. Достижение абсолютной одинаковости сводит моделирование к натурному эксперименту, о возможности или целесообразности которого было уже сказано. Остановимся на основных целях моделирования. Прогноз - оценка поведения системы при некотором сочетании ее управляемых и неуправляемых параметров. Прогноз - главная цель моделирования. Объяснение и лучшее понимание объектов. Здесь чаще других встречаются задачи оптимизации и анализа чувствительности. Оптимизация - это точное определение такого сочетания факторов и их величин, при котором обеспечиваются наилучший показатель качества системы, наилучшее по какому-либо критерию достижение цели моделируемой системой. Анализ чувствительности - выявление из большого числа факторов тех, которые в наибольшей степени влияют на функционирование моделируемой системы. Исходными данными при этом являются результаты экспериментов с моделью. Часто модель создается для применения в качестве средства обучения: модели-тренажеры, стенды, учения, деловые игры и т. п. Моделирование как метод познания применялось человечеством - осознанно или интуитивно - всегда. На стенах древних храмов предков южно-американских индейцев обнаружены графические модели мироздания. Учение о моделировании возникло в средние века. Выдающаяся роль в этом принадлежит Леонардо да Винчи (1452-1519). Гениальный полководец А. В. Суворов перед атакой крепости Измаил тренировал солдат на модели измаильской крепостной стены, построенной специально в тылу. Наш знаменитый механик-самоучка И. П. Кулибин (1735-1818) создал модель одноарочного деревянного моста через р. Неву, а также ряд металлических моделей мостов. Они были полностью технически обоснованы и получили высокую оценку российскими академиками Л. Эйлером и Д. Бернулли. К сожалению, ни один из этих мостов не был построен. Огромный вклад в укрепление обороноспособности нашей страны внесли работы по моделированию взрыва - генерал-инженер Н. Л. Кирпичев, моделированию в авиастроении - М. В. Келдыш, С. В. Ильюшин, А. Н. Туполев и др., моделированию ядерного взрыва - И. В. Курчатов, А.Д. Сахаров, Ю. Б. Ха-ритон и др. Широко известны работы Н. Н. Моисеева по моделированию систем управления. В частности, для проверки одного нового метода математического моделирования была создана математическая модель Синопского сражения - последнего сражения эпохи парусного флота. В 1833 году адмирал П. С. Нахимов разгромил главные силы турецкого флота. Моделирование на вычислительной машине показало, что Нахимов действовал практически безошибочно. Он настолько верно расставил свои корабли и нанес первый удар, что единственное спасение турок было отступление. Иного выхода у них не было. Они не отступили и были разгромлены. Сложность и громоздкость технических объектов, которые могут изучаться методами моделирования, практически неограниченны. В последние годы все крупные сооружения исследовалась на моделях - плотины, каналы, Братская и Красноярская ГЭС, системы дальних электропередач, образцы военных систем и др. объекты. Поучительный пример недооценки моделирования - гибель английского броненосца "Кэптен" в 1870 году. В стремлении еще больше увеличить свое тогдашнее морское могущество и подкрепить империалистические устремления в Англии был разработан суперброненосец "Кэптен". В него было вложено все, что нужно для "верховной власти" на море: тяжелая артиллерия во вращающихся башнях, мощная бортовая броня, усиленное парусное оснащение и очень низкими бортами - для меньшей уязвимости от снарядов противника. Консультант инженер Рид построил математическую модель устойчивости "Кэптена" и показал, что даже при незначительном ветре и волнении ему грозит опрокидывание. Но лорды Адмиралтейства настояли на строительстве корабля. На первом же учении после спуска на воду налетевший шквал перевернул броненосец. Погибли 523 моряка. В Лондоне на стене одного из соборов прикреплена бронзовая плита, напоминающая об этом событии и, добавим мы, о тупоумии самоуверенных лордов Британского Адмирал тейства, пренебрегших результатами моделирования. Этапы моделирования Математическое моделирование как, впрочем, и любое другое, считается искусством и наукой. Известный специалист в области имитационного моделирования Роберт Шеннон так назвал свою широко известную в научном и инженерном мире книгу: "Имитационное моделирование - искусство и наука". Поэтому в инженерной практике нет формализованной инструкции, как создавать модели. И, тем не менее, анализ приемов, которые используют разработчики моделей, позволяет усмотреть достаточно прозрачную этапность моделирования. Первый этап: уяснение целей моделирования. Вообще-то это главный этап любой деятельности. Цель существенным образом определяет содержание остальных этапов моделирования. Заметим, что различие между простой системой и сложной порождается не столько их сущностью, но и целями, которые ставит исследователь. Обычно целями моделирования являются:
Второй этап: построение концептуальной модели. Концептуальная модель (от лат. conception) - модель на уровне определяющего замысла, который формируется при изучении моделируемого объекта. На этом этапе исследуется объект, устанавливаются необходимые упрощения и аппроксимации. Выявляются существенные аспекты, исключаются второстепенные. Устанавливаются единицы измерения и диапазоны изменения переменных модели. Если возможно, то концептуальная модель представляется в виде известных и хорошо разработанных систем: массового обслуживания, управления, авторегулирования, разного рода автоматов и т. д. Концептуальная модель полностью подводит итог изучению проектной документации или экспериментальному обследованию моделируемого объекта. Результатом второго этапа является обобщенная схема модели, полностью подготовленная для математического описания - построения математической модели. Третий этап: выбор языка программирования или моделирования, разработка алгоритма и программы модели. Модель может быть аналитической или имитационной, или их сочетанием. В случае аналитической модели исследователь должен владеть методами решения. В истории математики (а это, впрочем, и есть история математического моделирования) есть много примеров тому, когда необходимость моделирования разного рода процессов приводила к новым открытиям. Например, необходимость моделирования движения привела к открытию и разработке дифференциального исчисления (Лейбниц и Ньютон) и соответствующих методов решения. Проблемы аналитического моделирования остойчивости кораблей привели академика Крылова А. Н. к созданию теории приближенных вычислений и аналоговой вычислительной машины. Результатом третьего этапа моделирования является программа, составленная на наиболее удобном для моделирования и исследования языке - универсальном или специальном. Четвертый этап: планирование эксперимента. Математическая модель является объектом эксперимента. Эксперимент должен быть в максимально возможной степени информативным, удовлетворять ограничениям, обеспечивать получение данных с необходимой точностью и достоверностью. Существует теория планирования эксперимента, нужные нам элементы этой теории мы изучим в соответствующем месте дисциплины. Результат четвертого этапа - план эксперимента. Пятый этап: выполнение эксперимента с моделью. Если модель аналитическая, то эксперимент сводится к выполнению расчетов при варьируемых исходных данных. При имитационном моделировании модель реализуется на ЭВМ с фиксацией и последующей обработкой получаемых данных. Эксперименты проводятся в соответствии с планом, который может быть включен в алгоритм модели. В современных системах моделирования такая возможность есть. Шестой этап: обработка, анализ и интерпретация данных эксперимента. В соответствии с целью моделирования применяются разнообразные методы обработки: определение разного рода характеристик случайных величин и процессов, выполнение анализов - дисперсионного, регрессионного, факторного и др. Многие из этих методов входят в системы моделирования (GPSS World, AnyLogic и др.) и могут применяться автоматически. Не исключено, что в ходе анализа полученных результатов модель может быть уточнена, дополнена или даже полностью пересмотрена. После анализа результатов моделирования осуществляется их интерпретация, то есть перевод результатов в термины предметной области. Это необходимо, так как обычно специалист предметной области (тот, кому нужны результаты исследований) не обладает терминологией математики и моделирования и может выполнять свои задачи, оперируя лишь хорошо знакомыми ему понятиями. На этом рассмотрение последовательности моделирования закончим, сделав весьма важный вывод о необходимости документирования результатов каждого этапа. Это необходимо в силу следующих причин. Во-первых, моделирование процесс итеративный, то есть с каждого этапа может осуществляться возврат на любой из предыдущих этапов для уточнения информации, необходимой на этом этапе, а документация может сохранить результаты, полученные на предыдущей итерации. Во-вторых, в случае исследования сложной системы в нем участвуют большие коллективы разработчиков, причем различные этапы выполняются различными коллективами. Поэтому результаты, полученные на каждом этапе, должны быть переносимы на последующие этапы, то есть иметь унифицированную форму представления и понятное другим заинтересованным специалистам содержание. В-третьих, результат каждого из этапов должен являться самоценным продуктом. Например, концептуальная модель может и не использоваться для дальнейшего преобразования в математическую модель, а являться описанием, хранящим информацию о системе, которое может использоваться как архив, в качестве средства обучения и т. д. Адекватность модели Итак, мы установили: модель предназначена для замены оригинала при исследованиях, которым подвергать оригинал нельзя или нецелесообразно. Но замена оригинала моделью возможна, если они в достаточной степени похожи или адекватны. Адекватность означает, достаточно ли хорошо с точки зрения целей исследования результаты, полученные в ходе моделирования, отражают истинное положение дел. Термин происходит от латинского adaequatus - приравненный. Говорят, что модель адекватна оригиналу, если при ее интерпретации возникает "портрет", в высокой степени сходный с оригиналом. До тех пор, пока не решен вопрос, правильно ли отображает модель исследуемую систему (то есть адекватна ли она), ценность модели нулевая! Термин "адекватность" как видно носит весьма расплывчатый смысл. Понятно, что результативность моделирования значительно возрастет, если при построении модели и переносе результатов с модели на систему - оригинал может воспользоваться некоторой теорией, уточняющей идею подобия, связанную с используемой процедурой моделирования. К сожалению теории, позволяющей оценить, адекватность математической модели и моделируемой системы нет, в отличие от хорошо разработанной теории подобия явлений одной и той же физической природы. Проверку адекватности проводят на всех этапах построения модели, начиная с самого первого этапа - концептуального анализа. Если описание системы будет составлено не адекватно реальной системе, то и модель, как бы точно она не отображала описание системы, не будет адекватной оригиналу. Здесь сказано "как бы точно", так как имеется в виду, что вообще не существуют математические модели, абсолютно точно отображающие процессы, существующие в реальности. Если изучение системы проведено качественно и концептуальная модель достаточно точно отражает реальное положение дел, то далее перед разработчиками стоит лишь проблема эквивалентного преобразования одного описания в другое. Итак, можно говорить об адекватности модели в любой ее форме и оригинала, если:
Предварительно исходный вариант математической модели подвергается следующим проверкам:
Такая предварительная оценка адекватности модели позволяет выявить в ней наиболее грубые ошибки. Но все эти рекомендации носят неформальный, рекомендательный характер. Формальных методов оценки адекватности не существует! Поэтому, в основном, качество модели (и в первую очередь степень ее адекватности системе) зависит от опыта, интуиции, эрудиции разработчика модели и других субъективных факторов. Окончательное суждение об адекватности модели может дать лишь практика, то есть сравнение модели с оригиналом на основе экспериментов с объектом и моделью. Модель и объект подвергаются одинаковым воздействиям и сравниваются их реакции. Если реакции одинаковы (в пределах допустимой точности), то делается вывод, что модель адекватна оригиналу. Однако надо иметь в виду следующее:
Для оценки степени подобия структур объектов (физических или математических) существует понятие изоморфизма (изо - одинаковый, равный, морфе - форма, греч.). Две системы изоморфны, если существует взаимно однозначное соответствие между элементами и отношениями (связями) этих систем. Изоморфны, например, множество действительных положительных чисел и множество их логарифмов. Каждому элементу одного множества - числу соответствует значение его логарифма в другом, умножению двух чисел в первом множестве - сложение их логарифмов в другом. C точки зрения пассажира план метрополитена, находящийся в каждом вагоне поезда метро, изоморфен реальному географическому расположению рельсовых путей и станций, хотя для рабочего, ремонтирующего рельсовые пути, этот план естественно не является изоморфным. Фотография является изоморфным отображением реального лица для милиционера, но не является таковым для художника. При моделировании сложных систем достигнуть такое полное соответствие трудно, да и нецелесообразно. При моделировании абсолютное подобие не имеет места. Стремятся лишь к тому. чтобы модель достаточно хорошо отражала исследуемую сторону функционирования объекта. Модель по сложности может стать аналогичной исследуемой системе и никакого упрощения исследования не будет. Для оценки подобия в поведении (функционировании) систем существует понятие изофункционализма. Две системы произвольной, а подчас неизвестной структуры изофункциональны, если при одинаковых воздействиях они проявляют одинаковые реакции. Такое моделирование называется функциональным или кибернетическим и в последние годы получает все большее распространение, например, при моделировании человеческого интеллекта (игра в шахматы, доказательство теорем, распознавание образов и т. д.). Функциональные модели не копируют структуры. Но копируя поведение, исследователи последовательно "подбираются" к познанию структур объектов (человеческого мозга, Солнца, и др.). Требования, предъявляемые к моделям Итак, общие требования к моделям.
Эти требования (обычно их называют внешними) выполнимы при условии обладания моделью внутренними свойствами. Модель должна быть:
Трудно ограничить область применения математического моделирования. При изучении и создании промышленных и военных систем практически всегда можно определить цели, ограничения и предусмотреть, чтобы конструкция или процесс подчинялись естественным, техническим и (или) экономическим законам. Круг аналогий, которые можно использовать в качестве моделей, также практически неограничен. Следовательно, надо постоянно расширять свое образование в конкретной области, но, в первую очередь, в математике. В последние десятилетия появились проблемы с неясными и противоречивыми целями, диктуемыми политическими и социальными факторами. Математическое моделирование в этой области пока еще проблематично. Что это за проблемы? Защита от загрязнения окружающей среды; предсказаний извержений вулканов, землетрясений, цунами; рост городов; руководство боевыми действиями и ряд других. Но, тем не менее, "процесс пошел", прогресс не остановим, и проблемы моделирования таких сверхсложных систем постоянно находят свое разрешение. Здесь следует отметить лидирующую роль отечественных ученых и, в первую очередь, академика Н. Н. Моисеева, его учеников и последователей.
2. Лекция: Типовые математические модели: версия для печати и PDA В этой теме рассматриваются элементы теории марковских процессов и ряд аналитических моделей, в основе которых лежит допущение о марковости протекающих в моделируемых объектах процессов. К таковым, в первую очередь, относится широкий класс самых разнообразных объектов, имеющих общее название систем массового обслуживания (СМО). Для ряда стандартных структур СМО аналитические модели, связывающие показатели эффективности СМО с характеристиками элементов СМО, приведены в соответствующих справочниках. Здесь же приводятся классификация СМО и приемы построения графов состояний СМО, позволяющих строить или применять готовые аналитические модели. Заметим, что для ряда современных сложных СМО аналитическое моделирование неприемлемо в силу недостаточности адекватных математических средств. В этих случаях следует применять имитационное моделирование, которое детально рассматривается в следующих темах. В многоэлементных системах с большим числом состояний аналитическое моделирование на основе теории марковских процессов становится весьма громоздким. В этом случае используется так называемый метод динамики средних, который в основе имеет также марковость процесса. Этот метод существенно упрощает аналитическое моделирование для случаев определения средних характеристик состояний моделируемой системы. В этой теме дано обоснование метода и приводятся примеры его применения. Схема гибели и размножения Часто в системах самого различного назначения протекают процессы, которые можно представить в виде модели "гибели и размножения". Граф состояний такого процесса показан на рис. 2.5.
Особенностью модели является наличие прямой и обратной связей с каждым соседним состоянием для всех средних состояний; первое и последнее (крайние) состояния связаны только с одним "соседом" (с последующим и предыдущим состояниями соответственно). Название модели - "гибель и размножение" - связано с представлением, что стрелки вправо означают переход к состояниям, связанным с ростом номера состояния ("рождение"), а стрелки влево - с убыванием номера состояний ("гибель"). Очевидно, стационарное состояние в этом процессе существует. Составлять уравнения Колмогорова нет необходимости, так как структура регулярна, необходимые формулы приводятся в справочниках, а также в рекомендованной литературе. Для приведенных на рис. 2.5 обозначений формулы имеют вид:
Пример 2.3. Имеется система из двух одинаковых и работающих параллельно компьютеров. Требуется определить надежностные характеристики этой системы. Решение В этой системе возможны три состояния:
Поскольку компьютеры одинаковые, то с точки зрения надежности, неважно, какой именно компьютер неисправен в состоянии С учетом сказанного, ситуация моделируется схемой "гибели и размножения" (рис. 2.6).
На рис. 2.6:
Пусть среднее время безотказной работы каждого компьютера
Тогда интенсивность отказов одного компьютера будет равна В состоянии
В состоянии
В состоянии
В состоянии
Используем зависимости (2.2). Вероятность состояния, когда обе машины исправны:
Вероятность второго состояния
Аналогично вычисляется и
|
||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 397; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.52.26 (0.014 с.) |


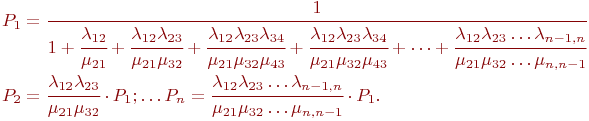
 - оба компьютера исправны;
- оба компьютера исправны; - один компьютер исправен, другой ремонтируется;
- один компьютер исправен, другой ремонтируется;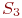 - оба компьютера неисправны и ремонтируются. Будем полагать, что процессы отказов и восстановлений - однородные марковские, одновременный выход из строя обоих компьютеров, как и одновременное восстановление двух отказавших компьютеров практически невозможно.
- оба компьютера неисправны и ремонтируются. Будем полагать, что процессы отказов и восстановлений - однородные марковские, одновременный выход из строя обоих компьютеров, как и одновременное восстановление двух отказавших компьютеров практически невозможно.
 ,
,  - интенсивности потоков отказов;
- интенсивности потоков отказов; - интенсивности потоков восстановлений.
- интенсивности потоков восстановлений. , а среднее время восстановления одного компьютера
, а среднее время восстановления одного компьютера  .
. , а интенсивность восстановления одного компьютера -
, а интенсивность восстановления одного компьютера - 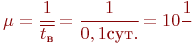 .
. работают оба компьютера, следовательно:
работают оба компьютера, следовательно:



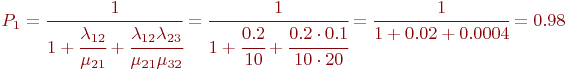

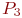 . Хотя найти
. Хотя найти 


