
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделирование полной группы несовместных событийСодержание книги
Поиск на нашем сайте
Элемент системы (или система в целом) может находиться во многих (больше двух) несовместных состояниях. Известны вероятности нахождения системы в этих состояниях. Например, средство вооружения может находиться:
Такие и аналогичные события называются полной группой несовместных событий. Алгоритм моделирования основан на следующей теореме. Теорема. В полной группе несовместных событий моделью свершения события
Доказател ьство Введем численные обозначения концов отрезков
В этом случае, согласно теореме, условием свершения события
Следовательно
Такой способ моделирования несовместных событий обычно называют определением исходов по жребию. Алгоритм, реализующий способ определения исходов по жребию, может быть построен тремя вариантами, представленными на рис. 3.16. Первый вариант (рис. 3.16а) применяется тогда, когда число возможных исходов невелико и не равно степени по основанию два. На рис. 3.16б алгоритм построен по способу половинных сечений для четырех исходов.
Третий вариант алгоритма (рис. 3.16в) в цикле определяет исход (событие), номер которого присваивается переменной Пример 3.8. Канал передачи данных может находиться в одном из четырех несовместных состояниях:
Решение Представим необходимые для определения исходов по жребию данные табл. 3.3.
Предположим, что при выполнении
|
|||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-24; просмотров: 224; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.226.17.3 (0.009 с.) |

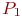 ;
; ;
;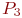 ;
; . Очевидно, что
. Очевидно, что  .
. , происходящего с вероятностью
, происходящего с вероятностью  , является попадание значения
, является попадание значения  в отрезок, равный
в отрезок, равный  , где
, где  - число несовместных событий (рис. 3.15):
- число несовместных событий (рис. 3.15):

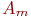 является:
является:
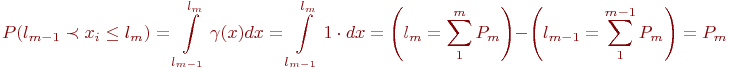

 . Далее этот номер используется для организации нужной работы алгоритма. Применение данного алгоритма будет показано в главе 6 (п. 6.7 и п. 6.8).
. Далее этот номер используется для организации нужной работы алгоритма. Применение данного алгоритма будет показано в главе 6 (п. 6.7 и п. 6.8). - исправен и свободен,
- исправен и свободен,  ;
; - исправен и занят,
- исправен и занят,  ;
; - неисправен,
- неисправен,  ;
; - подавлен помехами,
- подавлен помехами,  .
.
 )
)
 )
)
 -ой реализации датчик равномерно распределенных случайных чисел
-ой реализации датчик равномерно распределенных случайных чисел  сгенерировал
сгенерировал  . Путем последовательных сравнений определяется, что
. Путем последовательных сравнений определяется, что  . Значит в данной реализации канал находится в состоянии
. Значит в данной реализации канал находится в состоянии  - исправен и занят.
- исправен и занят.


