
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Деление отрезка в данном отношении.
3.Понятие об ур-нии линии.
Определение окружности и ее определение. Окружность радиуса R с центром в начале координат представляется уравнением
Уравнение прямой с угловым коэффициентом
5.Общее уравнение прямой.
Метод обратной матрицы решения системы алгебраических уравнений. m = n, det A ≠ 0 A×X = B Умножаем систему 2 слева на матрицу А-1 А-1 × А × Х = А-1 × В Е × Х = А-1 × В Х = А-1 × В 6.Ур-ние прямой, проходящей через 2 точки. Ур-ние прямой в отрезках.
Скалярные и векторные велечины. Сложение, вычетание векторов, умножение вектора на число.
15.Общее уравнение плоскости: Ах + Ву + Сz + D=0, где ABCD- некоторые числа, причем A2+B2+C2>0. 1. Уравнение плоскости по точке и нормальному вектору: M0M перпендикулярно 2. Уравнение плоскости в отрезках на осях: Ax+By+Cz =D, - 3.Уравнение плоскасти по трем точкам: 0=[M1M, M1M2, M1M3]- компланарные, M1M=(x-x1, y-y1, z-z1), M1M2=(x2-x1, y2-y1, z2-z1), M1M3=(x3-x1, y3-y1, z3-z1).
Угол между плоскостями: A1x + B1y + C1z + D1 = 0, A2x + B2y + C2z + D2 = 0.
Плоскости будут параллельны, если вектора калиниарны: n1⃓⃓ n2 ó A1x + B1y + C1z + D1=0. Плоскости перпендикулярны, когда вектора ортогональные:
Угол между 2-мя прямыми. Условия параллельности и перпендикулярности.
Угол между 2-мя векторами. Угол между векторами a1{X1;Y1;Z1},a2{X2;Y2;Z2} можно найти по формуле
Условие коллинеарности: Векторы назыв коллинеарными если они || одной плоскости Если векторы a1{X1;Y1;Z1},a2{X2;Y2;Z2} коллинеарны, то их соответствующие координаты пропорциональны X2: X1= Y2: Y1= Z2: Z и обратно. Если коэффициент пропорциональности положителен, то векторы равнонаправлены, если отрицателен, то – противопол направ. Условие компланарности: Три вектора назыв компланарными, если они, будучи приведены к одному началу, лежат в одной плоскости Условие (необходимое и достаточное) компланарности векторов a1{X1;Y1;Z1}, a2{X2;Y2;Z2},a3{X3;Y3;Z3}:
8. Кривые второго порядка (эллипс, парабола, гипербола) Парабола и ее свойства. Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax2, где х и у - текущие координаты, а- нек. число, наз. параболой.
y2=2px-симметрично отн. оси ОХ х2=2pу-симметрично отн. оси ОУ Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса. Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2 Св-ва: 1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax2.
Эллипс и его св-ва: Кривая второго порядка наз. эллипсом если коэффициенты А и L имеют одинаковые знаки Аx2+Cy2=d ур.-е наз. канонич. ур.-ем эллипса, где
Точки F1(-c,0) и F2(c,0) - наз. фокусами эллипса а. Отношение e=с/а наз. его эксцентриситетом (0<=e<=1) Точки A1,A2,B1,B2 -вершины эллипса. Св-во:
Гипербола и ее св-ва. Кривая 2го порядка наз. гиперболой, если в ур-ии Ax2+Cy2=d, коэффициент А и С имеют противоположные знаки, т.е. А*С<0 б) Если d>0, то каноническое ур-е гиперболы примет вид: x2/a2-y2/b2=1, F1(c,o) и F2(-c,0) - фокусы ее, e>0, e=c/a - эксцентриситет. Св-во: б) если d=0, ур-е примет вид x2/a2-y2/b2=0, получаем 2 перекрестные прямые х/а±у/b=0 в) если d<0, то x2/a2-y2/b2=-1 - ур-е сопряженной гиперболы.
Проекция вектора на ось Выражение «проекция вектора АВ на ось ОХ» употребляется в двух разных смыслах: геометрическом и алгебраическом (арифметическом). 1. Проекцией (геометрической) вектора АВ на ось ОХ называется вектор А'В', начало которого А' есть проекция начала А на ось ОХ, а конец В' — проекция конца В на ту же ось. Обозначение: Прох АВ или, короче, Пр АВ. Если ось ОХ задана вектором с, то вектор А'В' называется также проекцией вектора АВ на направление вектора с и обозначается Прс АВ. Геометрическая проекция вектора на ось ОХ называется также компонентой вектора по оси ОХ. 2. Проекцией (алгебраической) вектора АВ на ось ОХ (или на направление вектора с) называется длина вектора А'В', взятая со знаком + или -, смотря по тому, имеет ли вектор А'В' то же направление, что и ось ОХ (вектор с), или противоположное.
Обозначение: прох АВ или прс АВ. Замечание. Геометрическая проекция (компонента) вектора есть вектор, а алгебраическая проекция вектора есть число. Основные теоремы о проекциях вектора Теорема 1. Проекция суммы векторов на какую-либо ось равна сумме проекций слагаемых векторов на ту же ось. Теорема справедлива при обоих смыслах термина «проекция вектора» и при любом числе слагаемых; так, при трех слагаемых Пр ( а1 + а2 + а3) = Пр а1 + Пр а2 + Пр а3 (1) и np(а1 + а2 + а3) = пра1 + пра2 + пра3. (2) Теорема 2. Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором: пр. b = |b| cos (а^b). (3)
12.Операции над векторами: 1.Произведение вектора ā на число назыв вектор α*ā, модуль которого = |α|*|ā|, а направление совпадает с направлением вектора ā если α > 0 и противоположны ему если α<0 2.Анологичное правило для деления
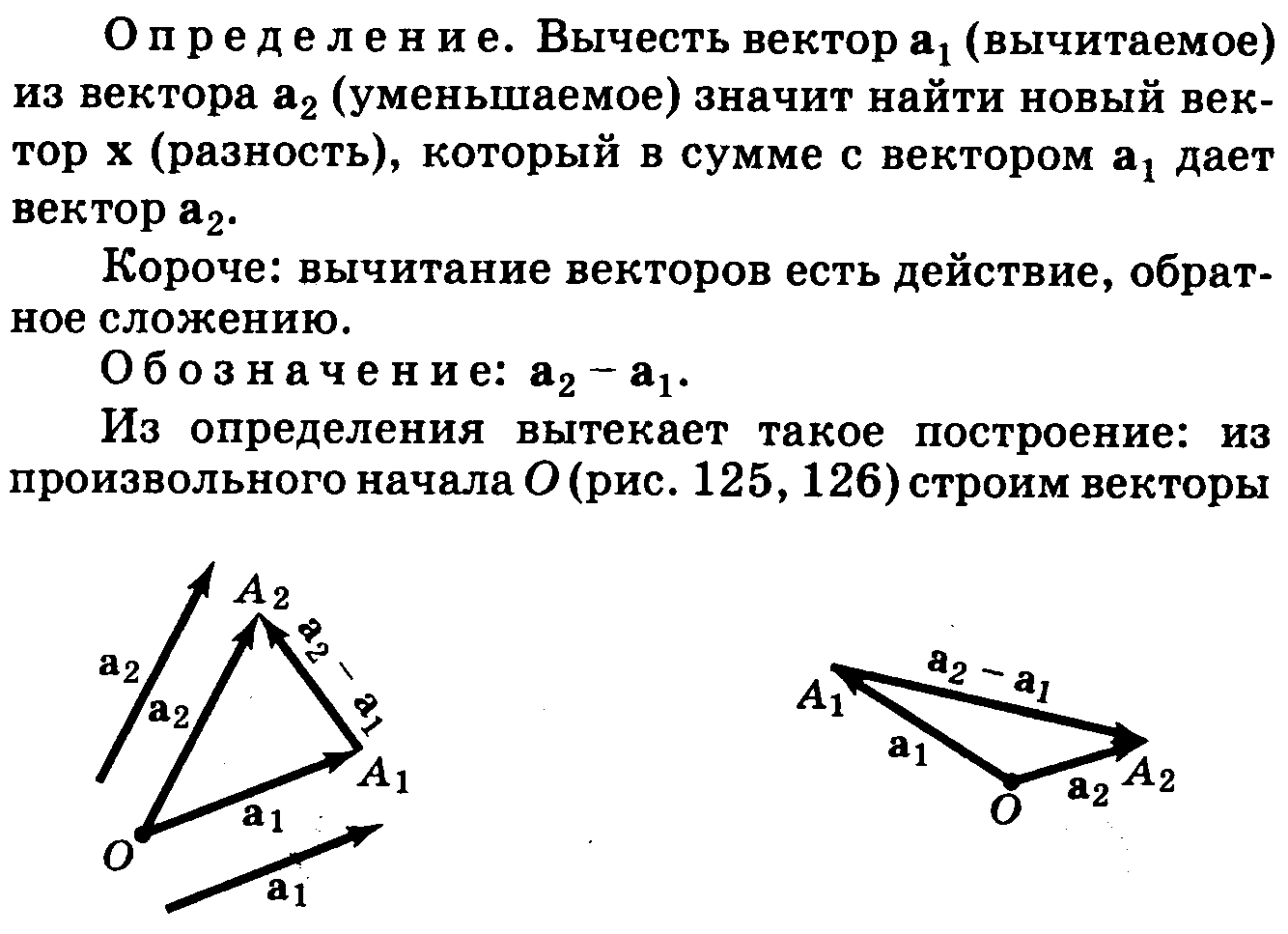
4.Анологичное правило для вычитания
|
||||||
|
Последнее изменение этой страницы: 2017-01-21; просмотров: 520; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.62.45 (0.028 с.) |




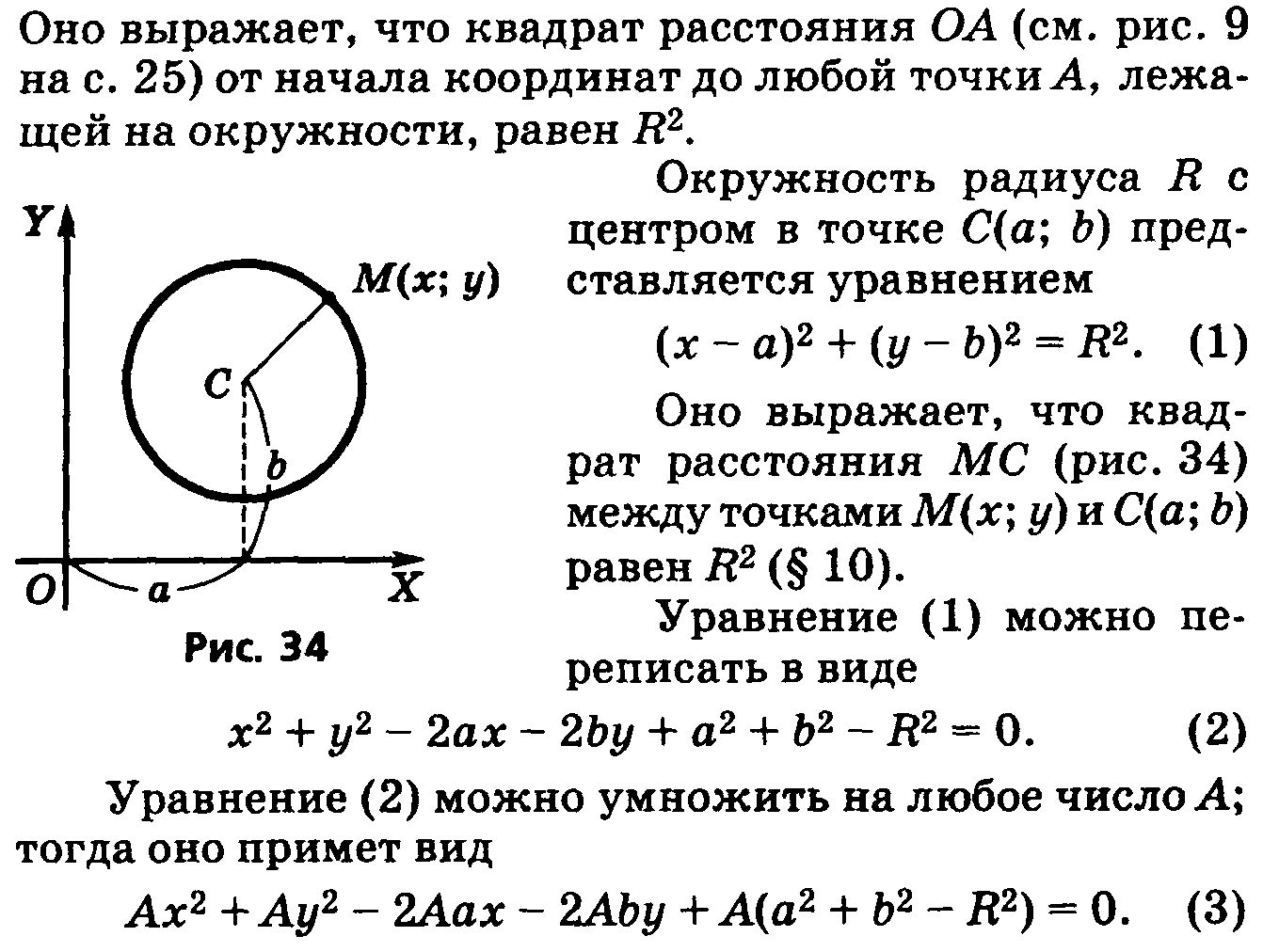













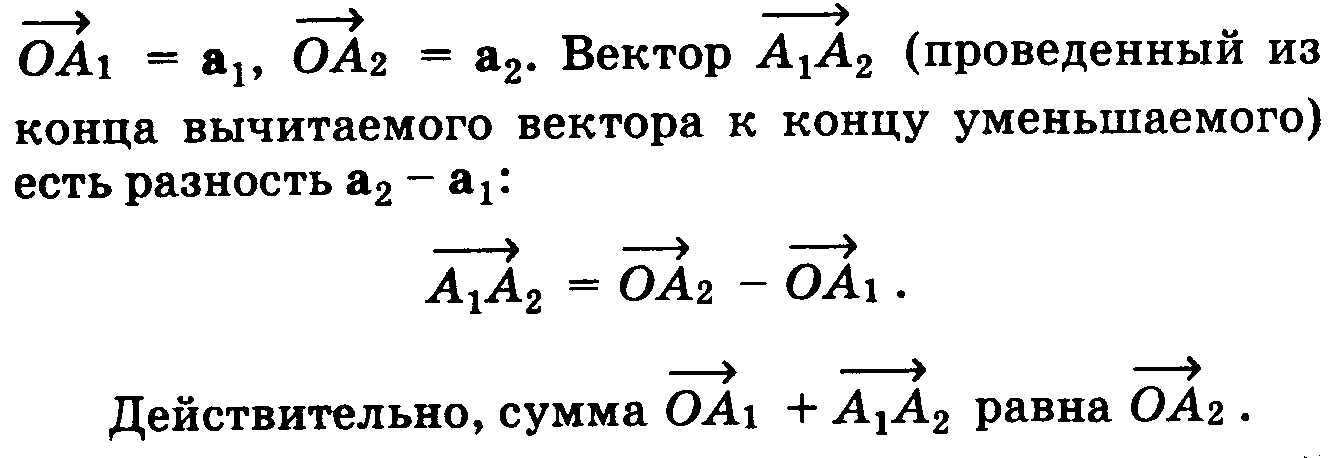

 ó
ó  -
- 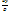 -
-  = 1,
= 1, 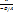 +
+  +
+  =1,
=1, 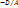 =a,
=a, 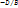 =b,
=b, 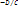 =c,
=c,  +
+  +
+  = 1.
= 1.
 =(A1, B1, C1 ),
=(A1, B1, C1 ),  =(A2, B2, C2)
=(A2, B2, C2)  =
= 
 =
=  =
=  ≠
≠ 
 =0, A1×A2 + B1×B2 + C1×C2 =0
=0, A1×A2 + B1×B2 + C1×C2 =0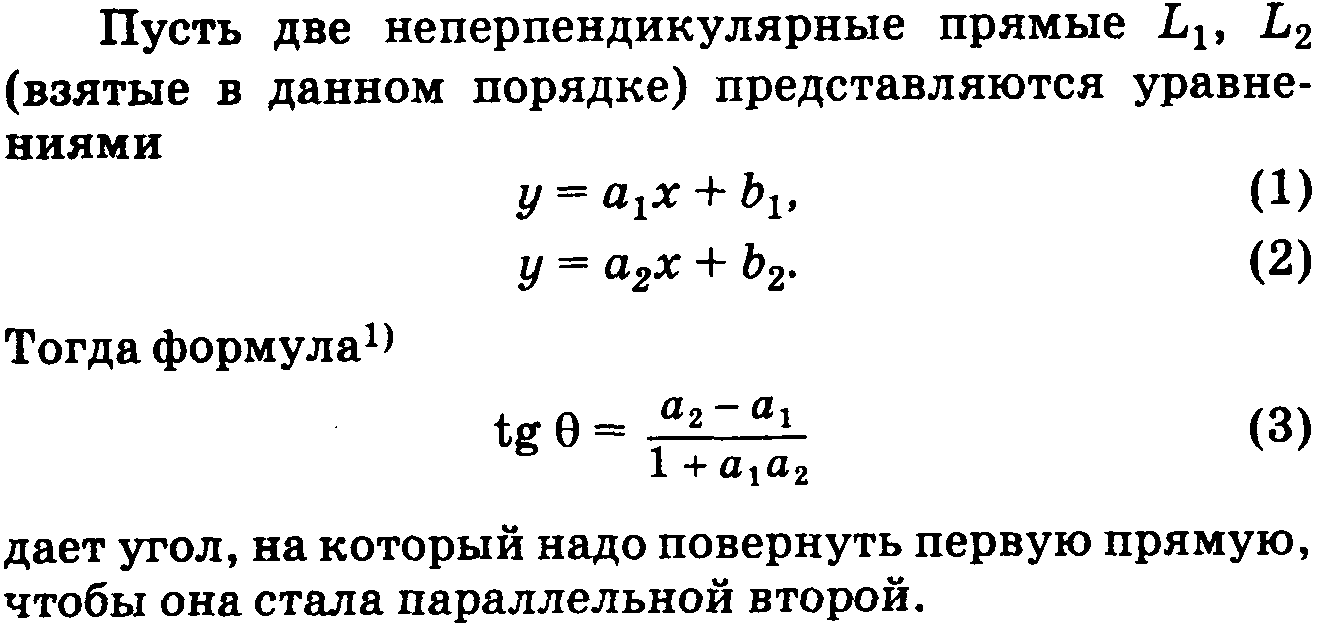









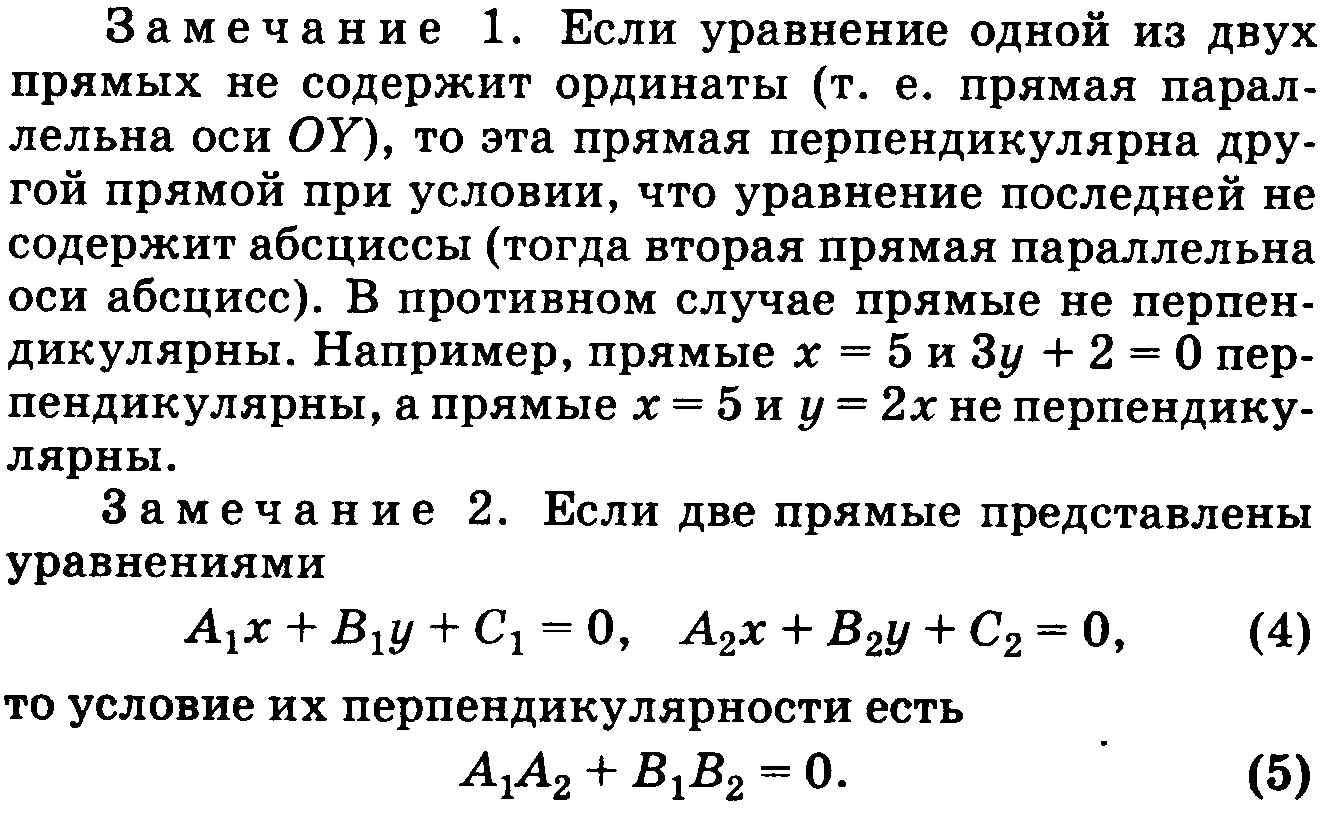


 Если вершина нах. в О(0,0), то ур-е примет вид
Если вершина нах. в О(0,0), то ур-е примет вид
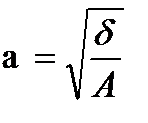
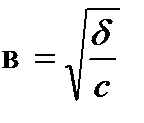 При а=в представляет собой ур-е окружности х2+y2=а2
При а=в представляет собой ур-е окружности х2+y2=а2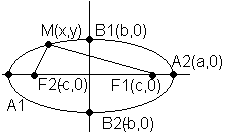
 3.Суммой векторов ā1,ā2,…,ān назыв вектор обознач ā1+ā2+…+ān= ā1, начало которого находится в начале вектора ān, ломаной линии составлен из последов слогаемых векторов (правило замыкания ломоной)
3.Суммой векторов ā1,ā2,…,ān назыв вектор обознач ā1+ā2+…+ān= ā1, начало которого находится в начале вектора ān, ломаной линии составлен из последов слогаемых векторов (правило замыкания ломоной)


