
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная ф-ции. Гео. и эк. Смысл.Содержание книги
Поиск на нашем сайте
Производной ф-ции y=f(x) в тч. Х0 наз. предел отношения приращения этой ф-ции к приращению аргумента, когда последнее стремится к нулю. Формула Правила дифференцирования: 2. Производная произведения двух диффиренц-ых ф-ций = произведению первой ф-ции на роизводную второй + произведение второй ф-ции на производную первой: 3. Производная частного двухдифференц-ых ф-ций определ. формулой: где Произв. Сложной и обр. ф-ции. Табл. Производных. Производная сложной ф.:Если
 - взимно-обратые дифференцируемые ф-ции и - взимно-обратые дифференцируемые ф-ции и 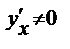 ,то ,то  Действительно,т.к. Действительно,т.к. 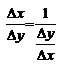 ,то ,то 
Таблица производной
Рассм. Ф-ию y=f(x), имеющую произв. в каждой точке ее обл. опр-я. Диф-лом ф-и y=f(x) наз. произведение произв-й этой ф-и на приращение независ. переменной х Диф-л независ. переем-й равен приращению этой переменной, поэтому диф-л ф-и равен произведению ее производной на диф-л незав. перем-ой.Геометр. смысл: диф-л ф-и равен приращению ординаты касательной к граф. Данной ф-и, когда аргумент получает приращение дельта х.
Бесконечно малое приращение ф-и эквивал. диф-лу этой ф-и при всех знач. незав. перем-ой, для кот-х произв-я ф-и конечна и отлична от нуля.f(x+дельтах)прибл.=f(x)+f’(x)*дельтаХ. Эта ф-ла позволяет вычислять прибл. знач-е ф-и, соотв-ее приращ-му знач. аргумента, если известно ее знач. в этой т. и знач. производной в этой т., когда приращение арг-та достаточно мало.
38.Теорема Ферма и Роля. Теорема Ферма: Если функция f(x) определена на интер(а, b) и в некот.точке x0 этого интервала имеет наибольшее или наименьшее значение, тогда если в точке х0 существует производная, то она равна нулю. Теорема Роля: Если функция y=f(x) непрерывна на отрезке [a, b] и дифференцируема внутри этого отрезка, причем f(a)=f(b), то существует по крайней мере одна точка x=c, принадлежащей отрезку (a, b), такая, что f’(c)=0 (касательная // OX)
39. Теорема Лагранжа: Если функция y=f(x) непрерывна на отрезке [a, b] и дифференцируема внутри этого отрезка, то существует по крайней мере одна точка с, принадлежащая отрезку (а, b), для которой справедлива формула: f(b)-f(a)/(b-a)=f”(c).Эта формула наз. Формулой конечных приращений Лагранжа.
40. Правило Лопиталя. Исп. при вычис.пределов для раскрытия неопредел.( Пример: lim sinx/x=lim (sinx)’/x’=lim cosx/1=1.
|
||||||
|
Последнее изменение этой страницы: 2017-01-21; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.162.87 (0.007 с.) |

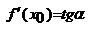 выражает геометрический смысл производной: производная от данной ф. в данной точке = tg угла наклона касательной графика ф-ции в этой тчк. Производительность труда есть производная объема продукции по времени. Рассмотрим некоторые понятия, иллюстрирующие экономический смысл производной. Пусть y(x) – ф-ция, характеризующая, например, издержки производства, где x - количество выпускаемой продукции. Тогда отношение
выражает геометрический смысл производной: производная от данной ф. в данной точке = tg угла наклона касательной графика ф-ции в этой тчк. Производительность труда есть производная объема продукции по времени. Рассмотрим некоторые понятия, иллюстрирующие экономический смысл производной. Пусть y(x) – ф-ция, характеризующая, например, издержки производства, где x - количество выпускаемой продукции. Тогда отношение  описывает средние издержки, приходящиеся на одно изделие. Средняя величина обозначается Ay или Af (от английского "average".) Среднее приращение, средний прирост, средняя скорость изменения определяется отношением
описывает средние издержки, приходящиеся на одно изделие. Средняя величина обозначается Ay или Af (от английского "average".) Среднее приращение, средний прирост, средняя скорость изменения определяется отношением  . Производная
. Производная 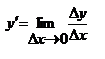 выражает предельные издержки производства. Величину Mf(x) = y' наз. мгновенным приростом или мгновенной скоростью изменения y. Аналогично можно определ. предельную выручку, предельный доход, предельную полезность и др. предельные величины.
выражает предельные издержки производства. Величину Mf(x) = y' наз. мгновенным приростом или мгновенной скоростью изменения y. Аналогично можно определ. предельную выручку, предельный доход, предельную полезность и др. предельные величины.



 и
и  -дифференцируемые ф. своих аргументов, то производная сложной ф.
-дифференцируемые ф. своих аргументов, то производная сложной ф.  сущ. и равна произведению производной этой ф-ции по промежуточному аргументу на производную промежуточного по независимой переменной, т.е.
сущ. и равна произведению производной этой ф-ции по промежуточному аргументу на производную промежуточного по независимой переменной, т.е. ,
,  .
. ,
,  ,
,  ,
, 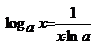
 ,
,  ,
,  ,
, 
 ,
, 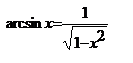 ,
, 
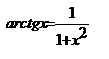 ,
, 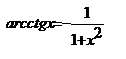 ,
,  ,
, 
 ,
, 
 37. Диф-л функции, его геометр. смысл. Приближенные выч-ия с пом. Диф-ла.
37. Диф-л функции, его геометр. смысл. Приближенные выч-ия с пом. Диф-ла.


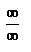 );(
);(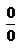 ). Теорема Лопиталя: Если ф-и у=f(х) и у=ф(х) удовлетв. услов. теор. Коши в нек.окрестн. х=
). Теорема Лопиталя: Если ф-и у=f(х) и у=ф(х) удовлетв. услов. теор. Коши в нек.окрестн. х=  ,стремят. к 0(
,стремят. к 0( ) при х
) при х 
 и сущ. lim
и сущ. lim 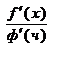 ,то сущ lim
,то сущ lim  и эти пределы равны.Пр.Лопиталя справедливо и при
и эти пределы равны.Пр.Лопиталя справедливо и при 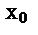 =
= 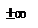 .
.


