
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Лопіталя. Розкриття невизначеностей виду
ТЕОРЕМА ЛОПІТАЛЯ. Нехай функції f(x) і
Сформульовану теорему прийнято називати правилом Лопіталя для розкриття невизначеностей виду якщо при деякому значенні Правило Лопіталя дозволяє звести обчислення границі відношення двох нескінченно малих (або двох нескінченно великих) функцій до границі відношення їхніх похідних, що у багатьох випадках є більш простою задачею. Може статися, що відношення похідних при Увага! Студент повинен з великою обережністю користуватися правилом Лопіталя: потрібно ділити похідну від чисельника на похідну від знаменника, взяті порізно, і в ніякому разі не диференціювати функцію як частку (як дріб). Ще одне суттєве зауваження, на яке слід акцентувати увагу студента. Із того, що границя Отже, хоча правило Лопіталя є ефективним методом обчислення границь, воно, на жаль, не завжди дає змогу досягти цілі. Підтвердимо це прикладом. Приклад. Знайти границю функції
Розв’язання. Застосування правила Лопіталя у даному випадку безрезультатне, оскільки відношення похідних цієї функції
не має границі при
Оскільки
(чисельник обмежений, а знаменник прямує до нескінченності). Існування границі заданої функції не суперечить теоремі Лопіталя, так як в ній стверджується, що коли відношення похідних прямує до границі, то до цієї границі прямує і відношення функцій, але не навпаки. Перейдемо до освоєння техніки обчислення границь, що ґрунтується на застосуванні правила Лопіталя.
2.2. Практика розкриття невизначеностей виду Користуючись правилом Лопіталя, знайти вказані границі: 1)
Примітка. Обчислення границі згідно з правилом Лопіталя зазвичай записують зразу. В існуванні необхідних похідних і границь переконуються безпосередньо в процесі обчислень. Тому попередні викладки можуть бути опущені, що й рекомендуємо робити в подальшому. 2) Розглянемо приклади, коли правило Лопіталя при знаходженні границі застосовується повторно. 4)
Остання границя при З огляду на сказане маємо а) б) Наведемо ще декілька прикладів, коли правило Лопіталя приходиться комбінувати з іншими методами знаходження границі. 6)
7)
Формула (1) залишається справедливою, коли відношення похідних прямує до нескінченності, тоді і відношення самих функцій також прямує до нескінченності.
Увага! Студент повинен розрізняти поняття «границя дорівнює Розглянемо два важливих приклади.
Таким чином, коли аргумент прямує до
2.3. Розкриття невизначеностей виду Під розкриттям невизначеності виду Під розкриттям невизначеності виду Такі невизначеності з допомогою алгебраїчних перетворень легко зводяться до основних –
Знайти границі: 1)
2)
4)
5) Оскільки
то вихідна границя
2.4. Степеневі невизначеності виду Такі невизначеності мають місце при розгляді степенево- показникової функції Перейдемо від степеневих невизначеностей до невизначеності
де функція f(x)>0, так як стоїть під знаком логарифма. Тепер можна записати
Знак границі і знак функції поміняли місцями, що припустимо внаслідок неперервності показникової функції. Задача звелася до знаходження границі добутку який є невизначеністю
Тоді остаточно для вихідної границі маємо
Знайти вказані границі: 1) Позначимо через А показник і знайдемо границю:
Отже, А=0. Повернемося до вихідної границі.
2)
Отже, А=0. В свою чергу, 3)
А=0. Остаточно для вихідної границі маємо
4)
Тепер можна повернутися до вихідної границі:
5)
Оскільки А=0, то 6)
Отже, остаточно дістанемо 7)
Повертаємося до вихідної границі: 8)
Оскільки 9)
У такому разі Зауваження. Можливий ще й такий спосіб розкриття невизначеностей: задану функцію попередньо логарифмуємо і знаходимо границю її логарифма, а потім уже за границею логарифма знаходимо границю самої функції. Покажемо це на прикладі. Знайдемо границю Прологарифмувавши обидві частини рівності, будемо мати
Таким чином,
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 534; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.111.9 (0.054 с.) |
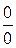 та
та 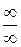 .
. визначені і диференційовні в околі точки
визначені і диференційовні в околі точки 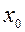 ,за винятком, можливо, самої точки
,за винятком, можливо, самої точки  і
і 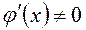 в цьому околі. Нехай також при
в цьому околі. Нехай також при  (або
(або 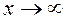 ) функції f(x) і
) функції f(x) і  спільно прямують до нуля або до нескінченності. Тоді якщо відношення їхніх похідних має границю, то відношення самих функцій також має границю, яка дорівнює границі відношення похідних, тобто
спільно прямують до нуля або до нескінченності. Тоді якщо відношення їхніх похідних має границю, то відношення самих функцій також має границю, яка дорівнює границі відношення похідних, тобто (1)
(1) (скінченному або нескінченному) границя відношення двох функцій є невизначеність виду
(скінченному або нескінченному) границя відношення двох функцій є невизначеність виду  або
або  .Тоді потрібно повторно скористатися правилом Лопіталя, виконуючи одночасно спрощення отриманих виразів, наприклад, скоротити спільні множники, або ж, спираючись на теореми про границі, звести задачу до знаходження вже знайомих границь. Більше того, правило Лопіталя можна застосовувати доти, поки не розкриється невизначеність. У цьому разі повторні застосування правила Лопіталя записують зазвичай в один ланцюжок рівностей.
.Тоді потрібно повторно скористатися правилом Лопіталя, виконуючи одночасно спрощення отриманих виразів, наприклад, скоротити спільні множники, або ж, спираючись на теореми про границі, звести задачу до знаходження вже знайомих границь. Більше того, правило Лопіталя можна застосовувати доти, поки не розкриється невизначеність. У цьому разі повторні застосування правила Лопіталя записують зазвичай в один ланцюжок рівностей.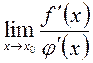 не існує, не можна робити висновок, що й шукана границя
не існує, не можна робити висновок, що й шукана границя  також не існує. Остання функція може існувати й тоді, коли відношення похідних при
також не існує. Остання функція може існувати й тоді, коли відношення похідних при  границі не має.
границі не має.

 . Порушено умову теореми Лопіталя. Проте границя даної функції знаходиться досить просто, а саме:
. Порушено умову теореми Лопіталя. Проте границя даної функції знаходиться досить просто, а саме: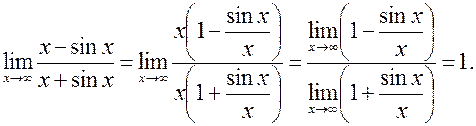
 . Увага! Тут не перша чудова границя.
. Увага! Тут не перша чудова границя.
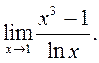 Безпосередня підстановка граничного значення аргументу x=1 приводить до невизначеності виду
Безпосередня підстановка граничного значення аргументу x=1 приводить до невизначеності виду 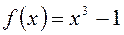 і
і  задовольняють умовам теореми Лопіталя, то згідно з (1) будемо мати
задовольняють умовам теореми Лопіталя, то згідно з (1) будемо мати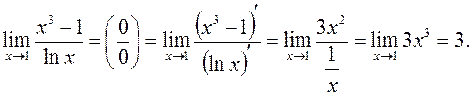
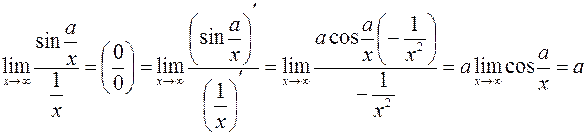 ,де a= const.
,де a= const. 



 При
При  , залишаючись додатним, маємо невизначеність виду
, залишаючись додатним, маємо невизначеність виду  яку потрібно розкрити. За правилом Лопіталя маємо
яку потрібно розкрити. За правилом Лопіталя маємо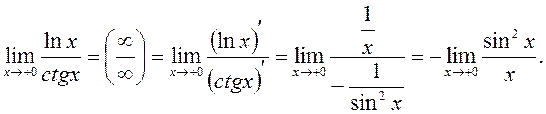
 дає невизначеність виду
дає невизначеність виду 



 .
.


 .
.

 » та «границя не існує».
» та «границя не існує».
 n – ціле додатне число.
n – ціле додатне число.
 , то степенева функція
, то степенева функція  (n>0) зростає швидше, ніж логарифмічна, а експонента – швидше ніж степенева.
(n>0) зростає швидше, ніж логарифмічна, а експонента – швидше ніж степенева. та
та  .
. розуміють знаходження границі
розуміють знаходження границі  якщо
якщо  і
і  де
де  розуміють знаходження границі
розуміють знаходження границі  коли
коли 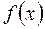 і
і  є нескінченно великі величини одного знаку.
є нескінченно великі величини одного знаку.
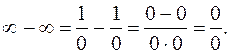
 В даному випадку має місце невизначеність виду
В даному випадку має місце невизначеність виду  дістанемо невизначеність виду
дістанемо невизначеність виду  яку розкриємо за правилом Лопіталя:
яку розкриємо за правилом Лопіталя:

 Тут невизначеність виду
Тут невизначеність виду  Щоб мати можливість застосовувати правило Лопіталя, запишемо добуток
Щоб мати можливість застосовувати правило Лопіталя, запишемо добуток  у вигляді частки
у вигляді частки  При
При  чисельник і знаменник цього дробу одночасно прямують до
чисельник і знаменник цього дробу одночасно прямують до  Таким чином, дістали невизначеність виду
Таким чином, дістали невизначеність виду 


 Так як
Так як 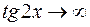 і
і  при
при  то маємо невизначеність виду
то маємо невизначеність виду 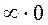 . Перетворимо даний вираз так:
. Перетворимо даний вираз так: 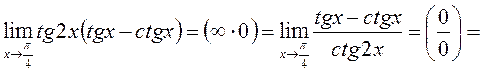

 При
При  маємо невизначеність виду
маємо невизначеність виду  Зведемо її до невизначеності виду
Зведемо її до невизначеності виду 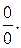




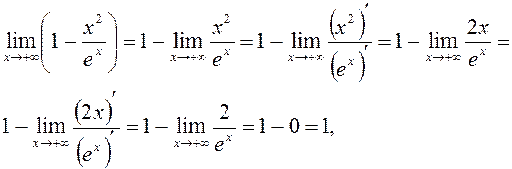


 коли f(x) прямує відповідно до
коли f(x) прямує відповідно до 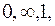 а
а  при
при 
 скориставшись логарифмічною тотожністю
скориставшись логарифмічною тотожністю  яка стосовно степенево-показникової функції набирає вигляду
яка стосовно степенево-показникової функції набирає вигляду або
або 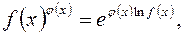





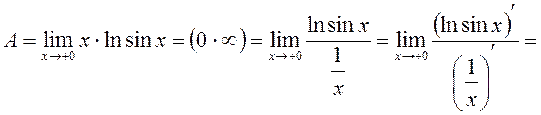






 .
.



 .
.
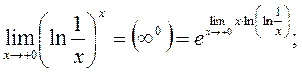


 .
.







 .
.




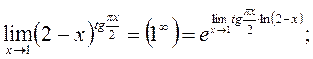
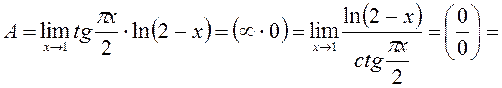

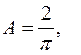 то
то 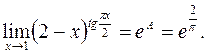


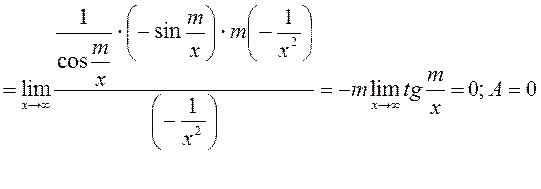
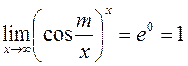 .
. яку позначимо через В:
яку позначимо через В: 
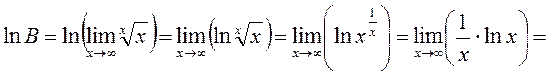

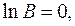 звідки вихідна границя В=1.
звідки вихідна границя В=1.


