
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Загальна схема дослідження функції та побудова її графіка
I. Елементарне дослідження функції. 1. Знайти ОВФ. 2. З’ясувати, чи не є функція парною, непарною або періодичною. 3. Знайти (якщо це не важко) точки перетину графіка з координатними осями. 4. Знайти точки розриву (якщо вони існують) та вияснити характер розривів. 5. Знайти асимптоти графіка функції або довести, що їх немає. II. Дослідження функції на монотонність та екстремум. 1. Знайти першу похідну функції та критичні точки 1-го роду. 2. На ОВФ допоміжного рисунка відмітити критичні точки, установити інтервали монотонності функції і на кожному із них методом пробних точок за знаком першої похідної з’ясувати зростає чи спадає функція. 3. Знайти точки екстремуму за зміною знака першої похідної при переході через критичну точку 1-го роду. 4. Обчислити екстремальні значення функції. 5. У випадку дослідження функції на екстремум за допомогою другої похідної, знайти другу похідну і скористатися другою достатньою ознакою екстремуму. III. Дослідження графіка функції на опуклість, угнутість та перегин. 1. Знайти другу похідну функції та критичні точки 2-го роду. 2. Нанести критичні точки 2-го роду на ОВФ допоміжного рисунка і установити інтервали опуклості, угнутості кривої. 3. Методом пробних точок за знаком другої похідної визначити опукла чи угнута крива на кожному із цих інтервалів. 4. Знайти абсциси точок перегину за зміною знака другої похідної при переході через критичну точку 2-го роду. 5. Знайти точки перегину. IV. Побудова графіка функції. 1. Побудувати графік функції, враховуючи результати проведених досліджень в розділах I-III. Зауваження. В процесі дослідження функції не обов’язково точно притримуватися наведеної схеми; інколи порядок дослідження зручно вибирати, виходячи із особливостей заданої функції. Більше того, при розв’язанні конкретної задачі окремі етапи цієї схеми можуть бути розширені, інші ж виявитися зайвими. Приклад 1. Дослідити функцію Розв’язання. 1) Це дробово-раціональна функція, яка визначена і неперервна на всій осі Ox за винятком точки x =-3. Отже, ОВФ:
4) Дослідимо поведінку функції поблизу точки розриву
Отже, є вертикальною асимптотою. Залишається дослідити, як веде себе функція, коли
Так як при 5) Шукаємо похилі асимптоти. Для того щоб вияснити, чи має графік функції похилі асимптоти, згадаємо, що коефіцієнти k та b рівняння
Маємо (границі при
Отже, З’ясуємо питання про взаємне розташування графіка функції і похилої асимптоти відносно один одного. Складемо різницю
Знайдемо знак
6) Знаходимо першу похідну даної функції:
7) Знаходимо критичні точки 1-го роду:
рис. 28).Цими точками та точкою розриву ОВФ ділиться на чотири інтервали монотонності: 9) Методом пробних точок визначимо, зростає чи спадає функція на кожному з цих інтервалів:
10) Дослідимо функцію на екстремум. При переході через точку 11) Обчислимо екстремальні значення функції:
12) Знаходимо другу похідну функції: 13) Визначимо, опукла чи угнута крива па кожному інтервалі:
14) На основі знайдених даних побудуємо графік функції в такій послідовності: насамперед відмітимо на осі Ox характерні точки (точку розриву, нулі функції, точки екстремуму). На площині Oxy відмітимо точки графіка, які відповідають виділеним значенням аргументу; проведемо вертикальну та похилу асимптоти. Характер Приклад 2. Дослідити функцію Розв’язання. 1) Функція визначена і неперервна на інтервалі 2) Функція ні парна, ні непарна; неперіодична. 3) Знаходимо точки перетину графіка з координатними осями: а) з віссю Ox:
Таким чином, пряма x =0 (вісь ординат) є вертикальна асимптота. Через те, що
Оскільки k=b= 0, то пряма y= 0 (вісь Ox) є горизонтальна асимптота. Відмітимо, що цей результат ми вже отримали раніше у п.4. 6) Знаходимо першу похідну даної функції
Інших критичних точок функція не має, так як існує в усіх точках ОВФ. 7)Відмічаємо цю єдину критичну точку на ОВФ (рис. 31). Вона розбиває область визначення на два інтервали монотонності: а) б)
а) б) 10) Знаходимо точки перегину. Оскільки при переході через критичну точку 2-го роду (з «-» на «+»), то точка
|
||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 415; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.149.32 (0.017 с.) |

 та побудувати її графік.
та побудувати її графік. 2) Так як ОВФ не симетрична відносно початку координат, то досліджувана функція ні парна, ні непарна; крім того, вона неперіодична. 3) Знайдемо точки перетину графіка функції з осями координат: а) з віссю Ox:
2) Так як ОВФ не симетрична відносно початку координат, то досліджувана функція ні парна, ні непарна; крім того, вона неперіодична. 3) Знайдемо точки перетину графіка функції з осями координат: а) з віссю Ox: 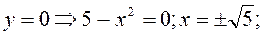
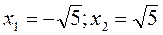 – нулі функції;
– нулі функції;  – точки перетину графіка функції з віссю Ox; б) з віссю Oy:
– точки перетину графіка функції з віссю Ox; б) з віссю Oy: 
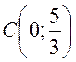 – точка перетину графіка функції з віссю Oy.
– точка перетину графіка функції з віссю Oy. . Знайдемо односторонні границі функції в точці
. Знайдемо односторонні границі функції в точці 
 є точка розриву 2-го роду, тому пряма
є точка розриву 2-го роду, тому пряма 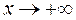 та
та  :
:
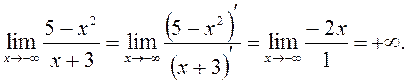
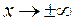 функція не має скінчених границь, то горизонтальних асимптот у даної кривої немає.
функція не має скінчених границь, то горизонтальних асимптот у даної кривої немає. знаходяться із співвідношень
знаходяться із співвідношень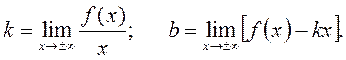


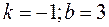 . Рівняння похилої асимптоти:
. Рівняння похилої асимптоти:  .
.
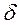 при
при  та
та 
 при
при  – крива розміщена під асимптотою.
– крива розміщена під асимптотою.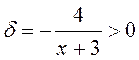 при
при  – крива розміщена над асимптотою.
– крива розміщена над асимптотою.

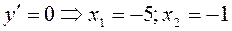 – критичні (стаціонарні) точки 1-го роду. Похідна терпить розрив при x =-3, але ця точка не входить в ОВФ.
– критичні (стаціонарні) точки 1-го роду. Похідна терпить розрив при x =-3, але ця точка не входить в ОВФ.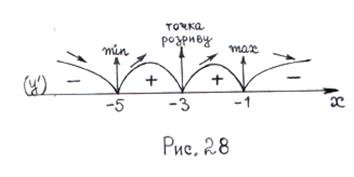 8) Відмічаємо критичні точки на ОВФ (дивись допоміжний
8) Відмічаємо критичні точки на ОВФ (дивись допоміжний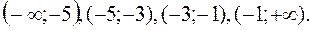
 – функція спадає на інтервалі
– функція спадає на інтервалі 
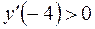 – функція зростає на інтервалі
– функція зростає на інтервалі 
 – функція зростає на інтервалі (–3;–1);
– функція зростає на інтервалі (–3;–1); – функція спадає на інтервалі
– функція спадає на інтервалі 
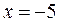 перша похідна змінює свій знак з «–» на «+», тому
перша похідна змінює свій знак з «–» на «+», тому 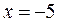 – це точка мінімуму. При переході через точку
– це точка мінімуму. При переході через точку 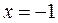 перша похідна змінює знак з «+» на «–», тому
перша похідна змінює знак з «+» на «–», тому 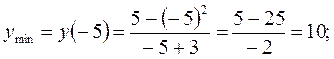

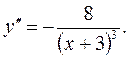 Друга похідна в нуль ніде не перетворюється і зазнає розриву при
Друга похідна в нуль ніде не перетворюється і зазнає розриву при 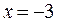 , але ця точка не входить в ОВФ. Критичних точок 2-го роду функція не має, тому друга похідна може змінювати знак тільки при переході через точку розриву
, але ця точка не входить в ОВФ. Критичних точок 2-го роду функція не має, тому друга похідна може змінювати знак тільки при переході через точку розриву  . Інтервали опуклості, угнутості (рис. 29):
. Інтервали опуклості, угнутості (рис. 29): 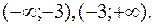
 – крива угнута на інтервалі
– крива угнута на інтервалі 
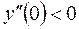 – крива опукла на інтервалі
– крива опукла на інтервалі 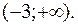 Точок перегину функція не має.
Точок перегину функція не має.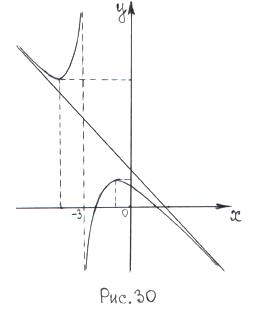 точки розриву визначає вигляд кривої поблизу цієї точки. Знання інтервалів зростання та спадання функції, інтервалів опуклості, угнутості допоможе нам точніше побудувати графік даної функції (дивись рис. 30).
точки розриву визначає вигляд кривої поблизу цієї точки. Знання інтервалів зростання та спадання функції, інтервалів опуклості, угнутості допоможе нам точніше побудувати графік даної функції (дивись рис. 30).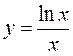 і побудувати її графік.
і побудувати її графік.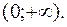
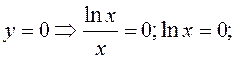
 – нуль функції; А(1;0) – точка перетину з віссю Ox; б) з віссю Oy точок перетину графік не має, бо x =0 не належить ОВФ. 4) Досліджуємо поведінку функції на границі її області визначення. Якщо
– нуль функції; А(1;0) – точка перетину з віссю Ox; б) з віссю Oy точок перетину графік не має, бо x =0 не належить ОВФ. 4) Досліджуємо поведінку функції на границі її області визначення. Якщо  , залишаючись додатним, то
, залишаючись додатним, то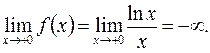 Це випливає з того, що
Це випливає з того, що 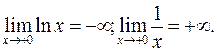
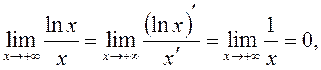 то пряма y =0 (вісь Ox) є горизонтальна асимптота. 5) Шукаємо похилі асимптоти y=kx+b. Ліва похила асимптота відсутня, так як неможливо, щоб
то пряма y =0 (вісь Ox) є горизонтальна асимптота. 5) Шукаємо похилі асимптоти y=kx+b. Ліва похила асимптота відсутня, так як неможливо, щоб  Маємо
Маємо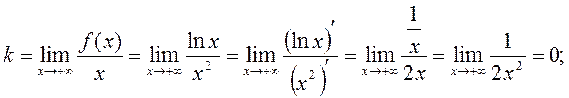
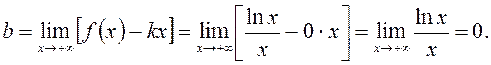
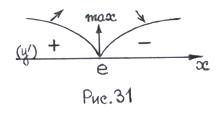
 та критичні точки 1-го роду з умови
та критичні точки 1-го роду з умови 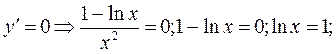 x=e – стаціонарна точка.
x=e – стаціонарна точка.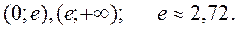 Методом пробних точок дослідимо знак похідної
Методом пробних точок дослідимо знак похідної  на кожному з цих інтервалів:
на кожному з цих інтервалів: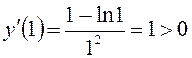 – функція зростає на інтервалі (0; е);
– функція зростає на інтервалі (0; е); – функція спадає на інтервалі
– функція спадає на інтервалі 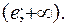 8) Перевіряємо достатні умови екстремуму. Перша похідна
8) Перевіряємо достатні умови екстремуму. Перша похідна 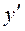 , як неперервна функція на ОВФ, змінює знак з «+» на «-», коли x переходить через стаціонарну точку x=e. А це означає, що точка x=e є точкою максимуму функції. Легко пересвідчитись, що
, як неперервна функція на ОВФ, змінює знак з «+» на «-», коли x переходить через стаціонарну точку x=e. А це означає, що точка x=e є точкою максимуму функції. Легко пересвідчитись, що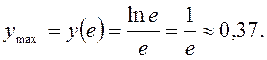 9)Щоб дослідити графік функції на опуклість, угнутість, знайдемо другу похідну:
9)Щоб дослідити графік функції на опуклість, угнутість, знайдемо другу похідну: 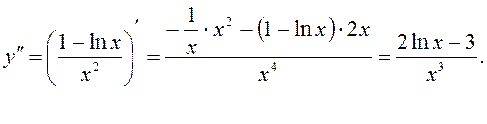 Вона неперервна на ОВФ. Прирівнюючи
Вона неперервна на ОВФ. Прирівнюючи  до нуля, знаходимо критичні точки 2-го роду функції:
до нуля, знаходимо критичні точки 2-го роду функції: 
 –
– 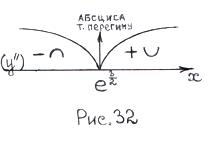 критична точка 2-го роду. Ця точка розбиває ОВФ на два інтервали опуклості, угнутості (дивись рис. 32):
критична точка 2-го роду. Ця точка розбиває ОВФ на два інтервали опуклості, угнутості (дивись рис. 32):  У кожному із них друга похідна зберігає певний знак. Щоб з’ясувати, який саме, скористаємося методом пробних точок:
У кожному із них друга похідна зберігає певний знак. Щоб з’ясувати, який саме, скористаємося методом пробних точок: – функція опукла на інтервалі
– функція опукла на інтервалі 
 – функція угнута на інтервалі
– функція угнута на інтервалі 
 відбувається зміна знака другої похідної
відбувається зміна знака другої похідної – абсциса точки перегину.
– абсциса точки перегину. Р(4,49;0,33) – точка перегину даної функції. 11) Враховуючи всі отримані результати дослідження, будуємо графік функції
Р(4,49;0,33) – точка перегину даної функції. 11) Враховуючи всі отримані результати дослідження, будуємо графік функції 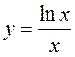 (рис.33).
(рис.33).


