
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні правила і формули диференціюванняСтр 1 из 9Следующая ⇒
ДИФЕРЕНЦІЮВАННЯ Література: Поняття похідної Поняття похідної – фундаментальне поняття математичного аналізу, за допомогою якого досліджуються процеси і явища в природничих, соціальних та економічних науках. Зокрема, при застосуванні таких економічних понять, як попит, витрати виробництва, національний прибуток тощо, часто доводиться визначати швидкість зміни значень відповідних величин. Розв’язання таких задач ґрунтується на методах диференціального числення. Тому вивченню похідної слід приділити особливу увагу. Нехай функція y=f(x) визначена і неперервна в деякому проміжку і нехай довільне значення Означення. Похідною функції За означенням
Позначають так: Термін «похідна» запровадив французький математик Лагранж. Якщо в точці Якщо границя (1) існує в кожній точці деякого проміжку, то похідна є функцією від Функцію, яка має скінченну похідну в точці ТЕОРЕМА. Якщо функція Обернене твердження, взагалі кажучи, не має місця, тобто з неперервності функції Отже, неперервність функції в точці є лише необхідною умовою її диференційовності в цій точці. Геометричний зміст похідної. Значення похідної
Механічний зміст похідної. Якщо функція Узагальнюючи, можна сказати так: якщо функція Економічний зміст похідної пояснимо на прикладі. Якщо позначити через
1.2. Безпосереднє диференціювання
Якщо похідна даної функції знаходиться згідно з означенням (за формулою (1)), тобто шляхом послідовного визначення Приклад 1. Користуючись способом безпосереднього диференціювання, знайти похідну функції Розв’язання. При значенні аргументу, що дорівнює
Складаємо відношення Знаходимо границю відношення
Приклад 2. Виходячи з означення похідної, знайти похідну функції Розв’язання. Знаходимо приріст функції
Складаємо відношення
Таблиця похідних основних елементарних функцій
Доцільно ще раз підкреслити, що оскільки, по суті, на основі однієї цієї формули здійснюється диференціювання будь-якого виразу, то студенти не тільки повинні пам’ятати її напам’ять, але й уміти прочитати її словесно. Якщо складена функція містить декілька проміжних аргументів, наприклад,
Це правило поширюється і на складені функції, які задаються ланцюжком із довільного скінченого числа проміжних аргументів. У цьому разі потрібно виконати наступні дії:
1) визначити вид складеної функції (функція якого виду – степеневого, логарифмічного, показникового, тригонометричного чи обернено тригонометричного); 2) занумерувати проміжні аргументи; 3) необхідне число разів скористатися правилом диференціювання складеної функції.
Монотонність функції Нехай функція y=f(x) визначена на деякому інтервалі (a;b). Звернемося до рис.1, нагадавши одночасно геометричний зміст похідної функції y=f(x) точці x:
Означення. Функція f(x) називається зростаючою (спадною) на інтервалі (a;b), якщо на цьому інтервалі більшому значенню аргументу відповідає більше (менше) значення функції, тобто
Означення. Функція f(x) називається монотонною на інтервалі (a;b), якщо вона на цьому інтервалі або тільки зростає, або тільки спадає. Наприклад, показникова функція Увага! Надалі студент повинен чітко розуміти різницю між необхідними та достатніми умовами зростання та спадання функції тощо. Для цього слід більш детально зупинитися на поняттях необхідної і достатньої умови. Умова називається необхідною для даної обставини, якщо завжди, коли дана обставина має місце, ця умова виконується. Умова називається достатньою, якщо кожного разу, коли вона виконується, дана обставина має місце. Наприклад, подільність деякого числа k на 2 необхідна (але не достатня) для його подільності на 6, а подільність на 6 достатня (але не необхідна) для його подільності на 2. Дійсно, із того що число ділиться на 6 випливає його подільність на 2. Таким чином, для того щоб число ділилось на 6, необхідна його парність. Ясно, що не всяке парне число ділиться на 6 (тобто ця умова не є достатньою). Зростання та спадання функції характеризується знаком її похідної. Сформулюємо аналітичну ознаку (критерій) зростання та спадання функції. ТЕОРЕМА 1 (необхідна ознака монотонності функції). 1. Якщо функція f(x) на інтервалі (a;b) диференційовна і зростає, то її похідна невід’ємна на цьому інтервалі, тобто
2. Якщо функція f(x) на інтервалі (a;b) диференційовна і спадає, то її похідна недодатна на цьому інтервалі, тобто
Геометричний зміст щойно наведеної теореми очевидний і випливає з геометричного змісту похідної: 1) дотична до графіка зростаючої функції утворює з додатним напрямом осі Ox гострий кут або (в окремих точках) горизонтальна Що нам дає теорема 1? Теорема 1 дозволяє за характером росту монотонної в інтервалі функції установити знак її похідної в цьому інтервалі. Проте, коли ми тільки починаємо досліджувати функцію, то її поведінка, як правило, нам невідома. Тому для нас значно важливіше сформулювати таку умову, виконання якої гарантує, що функція зростає (спадає) на деякому проміжку; інакше кажучи, сформулювати достатню умову монотонності функції.
ТЕОРЕМА 2 (достатня ознака монотонності функції). Якщо функція f(x) в кожній точці інтервалу (a;b) має додатну (від’ємну) похідну, то сама функція зростає (спадає) на цьому інтервалі. Унаочнимо сказане такою табличкою:
Геометрично ясно, що функція буде монотонною і в тому випадку, коли її похідна, зберігаючи весь час сталий знак, в окремих точках дорівнює нулю. Теореми 1 і 2 – це чисто аналітичні ознаки, які знаходяться у повній погодженості з тими висновками, які ми зробили із спостережень над кривою на початку параграфа (дивись рис.1). Зауваження. Ми не ввели поняття зростаючої та спадної функції в точці. Водночас не запровадили більш детальної класифікації функцій стосовно характеру їхньої поведінки на інтервалі, а саме: зростаюча, спадна, незростаюча, неспадна. І нарешті, на основі цієї класифікації не сформулювали відповідні ознаки поведінки функції. Вичерпну відповідь на ці питання студент може знайти, скориставшись такими навчальними посібниками: 1. Суліма І.М., Ковтун І.І., Яковенко В.М. Вища математика, ч.2, НАУ, Київ, 2003. 2. Валєєв К.Г., Джалладова І.А. Вища математика, ч.1, КНЕУ, Київ,2001. Означення. Інтервалами або проміжками монотонності функції f(x) називаються інтервалами її області визначення, на яких функція або тільки зростає, або тільки спадає. Ознакою інтервалу монотонності є зберігання знака похідної функції на цьому інтервалі
Звернувшись до рис.2, бачимо, що інтервали монотонності можуть відділятися один від одного або точками, де похідна функції дорівнює нулю (їх називають стаціонарними точками), або точками, де похідна дорівнює нескінченності чи не існує. І, нарешті, це можуть бути точки розриву функції. Відмітимо, що коли похідна не існує в якійсь точці (але існує в сусідніх точках), то в цій точці похідна розривна. В стаціонарних точках дотична до графіка функції паралельна осі Ox (на рис. 2 це точки Увага! Не кожна стаціонарна точка відділяє інтервали монотонності (на рис.2 це точки
Означення. Критичними точками 1-го роду функції f(x) називають точки, розташовані всередині її області визначення, в яких похідна Зазначимо, що критичні точки включають в себе і стаціонарні точки. В стаціонарних точках миттєва швидкість зміни функції дорівнює нулю, тобто це ніби точки миттєвого спокою. ПРАВИЛО ЗНАХОДЖЕННЯ ІНТЕРВАЛІВ МОНОТОННОСТІ ФУНКЦІЇ f(x):
Приклад 1. Знайти інтервали монотонності функції
Розв’язання. 1) Функція визначена і диференційована на інтервалі 3) Знаходимо критичні точки 1-го роду:
Інших критичних точок немає, так як
Вони розбивають ОВФ на три інтервали: Нанесемо на рис. 3 результати дослідження знака похідної на інтервалах монотонності. Стрілками, звернутими вгору і вниз, показано поводження функції на цих інтервалах. Приклад 2. Знайти інтервали зростання і спадання функції Розв’язання. 1) Функція визначена і диференційована на множині дійсних чисел, крім точки x= 1 (так як знаменник не повинен перетворюватися в нуль). Точка x= 1 – точка розриву функції. Тому ОВФ:
5) Визначаємо знак похідної на кожному інтервалі. Маємо
Результати визначення знака похідної нанесемо на рис. 4.
Екстремум функції Більшість елементарних функцій не є монотонними всюди, де вони визначені. ОВФ часто містить як проміжки зростання, так і проміжки спадання функції. Особливу зацікавленість викликають «примежові» значення аргументу (на рис. 2 це точки
Нехай функція y=f(x) визначена на інтервалі функція f(x) має максимум (мінімум) у точці Точка Позначають так: 1) максимум – max (скорочення латинського «найбільший»); 2) мінімум – min (скорочення латинського «найменший»); 3) екстремум – extr (скорочення латинського «крайній»). Точку В економічних дисциплінах екстремум функції називають її локальним оптимумом, а процес знаходження екстремального значення функції називають оптимізацією.
Рис. 5 ілюструє деякі характерні випадки поведінки функції в околі екстремальної точки. Звернемо увагу на такі обставини. 1.Якщо функція визначена на відрізку 2.Поняття екстремуму носить локальний (місцевий) характер і завжди зв’язане з поведінкою функції тільки в деякому околі точки із ОВФ, а не з усією ОВФ. Окремі min можуть бути навіть більшими деяких max функції (дивись рис. 2)Тому не слід плутати max і min функції з її найбільшим та найменшим значенням в ОВФ. З’ясуємо умови існування екстремуму. ТЕОРЕМА 3 (необхідна ознака екстремуму). Якщо у точці
Коментарі до теореми 3. 1. Умова 2. Точки екстремуму функції є її критичними точками 1-го роду. Це зразу звужує множину точок, серед яких можуть знаходитись точки екстремуму. Обернене твердження невірне: не всяка критична точка функції є її екстремальною точкою. Так, наприклад, для функції Проте ця точка не є екстремальною, що видно з графіка цієї функції (див. рис. 17). У зв’язку з цим критичні точки іноді називають точками, «підозрілими» на екстремум або точками можливого екстремуму, тому що екстремальні точки потрібно шукати лише серед них. В практичних задачах функція має зазвичай всього декілька критичних точок. Розглянемо критерії, які дають змогу із множини критичних точок виділити точки екстремуму. Перша достатня ознака екстремуму (перше правило). Нехай функція y=f(x) диференційована в околі критичної точки 1-го роду 1) якщо при переході через точку
3) якщо похідна
Приклад 1. Знайти інтервали монотонності та дослідити на екстремум функцію Розв’язання. Використаємо вище наведене правило. 1) ОВФ: 3) Знаходимо критичні точки 1-го роду:
5) Визначаємо знак похідної на кожному інтервалі за знаком похідної у пробній точці інтервалу:
6) При переході через стаціонарну точку «–» на «+», тому точка
А(-1;1) і О(0;0) – точки на графіку функції, де вона має max і min відповідно. 8) Будуємо ескіз графіка функції (дивись рис.9). У більш– менш складних прикладах визначити знак похідної у пробних точках досить трудно. Щоб «обійти» ці труднощі, в окремих випадках можна скористатися іншим способом дослідження функції на екстремум. Сформулюємо так звану другу достатню ознаку екстремуму, яка інколи виявляється зручнішою і простішою, ніж перша достатня ознака. Друга достатня ознака екстремуму (друге правило). Нехай в околі стаціонарної точки Якщо Якщо При Унаочнює другу достатню ознаку так зване правило «ковшика»:
Правило знаходження екстремуму функції за допомогою другої похідної:
Приклад 2. Дослідити на екстремум функцію Розв’язання. 1) Задана функція всюди неперервно диференційовна. Знайдемо її першу похідну:
2) Шукаємо стаціонарні точки із умови Стаціонарні точки будуть такими: 3) Знайдемо другу похідну:
4) Досліджуємо знак другої похідної в стаціонарних точках:
Отже, 5) Обчислимо екстремальні значення функції:
Примітка. Що стосується стаціонарної точки
Точки перегину Нехайкрива, що задана рівнянням y=f(x), гладка на деякому інтервалі (a;b), тобто функція f(x) неперервна і неперервно диференційовна на цьому інтервалі. Тоді в кожній точці такої кривої можна провести дотичну.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-26; просмотров: 198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.190.156.80 (0.132 с.) |
 § 21;
§ 21;  гл.5, § 1-2.
гл.5, § 1-2.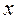 і точка
і точка  належать цьому проміжку. Знайдемо відповідний приріст функції
належать цьому проміжку. Знайдемо відповідний приріст функції 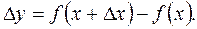 Тоді відношення
Тоді відношення 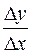 характеризує середню швидкість зміни функції на відрізку
характеризує середню швидкість зміни функції на відрізку 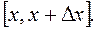 Щоб дістати більш точну характеристику зміни функції, розглянемо
Щоб дістати більш точну характеристику зміни функції, розглянемо 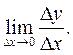 Якщо ця границя існує, то вона характеризує швидкість зміни функції в точці
Якщо ця границя існує, то вона характеризує швидкість зміни функції в точці 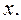
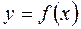 в точці x називається границя відношення приросту функції
в точці x називається границя відношення приросту функції 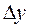 в цій точці до приросту аргументу, коли приріст аргументу прямує до нуля.
в цій точці до приросту аргументу, коли приріст аргументу прямує до нуля. 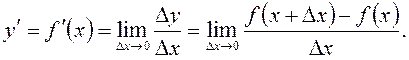 (1)
(1)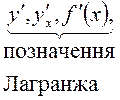
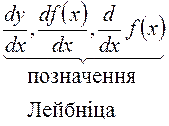

 то
то 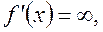 якщо ж ця границя не існує, то не існує в цій точці і похідної.
якщо ж ця границя не існує, то не існує в цій точці і похідної.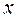 в цьому проміжку. Для даного фіксованого значення аргументу
в цьому проміжку. Для даного фіксованого значення аргументу 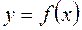 диференційовна в точці
диференційовна в точці  , то вона неперервна в цій точці.
, то вона неперервна в цій точці.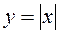 неперервна в точці
неперервна в точці 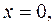 але вона не має в цій точці похідної.
але вона не має в цій точці похідної. 
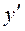 в точці
в точці  Отже,
Отже, 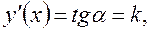 де
де 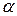 – кут нахилу дотичної.
– кут нахилу дотичної.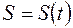 описує закон прямолінійного руху матеріальної точки, де
описує закон прямолінійного руху матеріальної точки, де  – шлях,
– шлях, 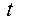 – час, то швидкість
– час, то швидкість 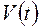 в даний момент часу – це похідна від пройденого шляху
в даний момент часу – це похідна від пройденого шляху 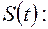

 описує деякий фізичний процес, то похідна
описує деякий фізичний процес, то похідна 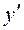 є швидкістю зміни цього процесу. В цьому полягає фізичний зміст похідної.
є швидкістю зміни цього процесу. В цьому полягає фізичний зміст похідної.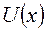 прибуток від продажу
прибуток від продажу 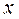 одиниць товару, то границя
одиниць товару, то границя  називається маргінальним (граничним) прибутком.
називається маргінальним (граничним) прибутком. і
і 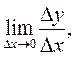 то такий спосіб знаходження похідної називається безпосереднім диференціюванням.
то такий спосіб знаходження похідної називається безпосереднім диференціюванням.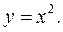 Обчислити
Обчислити 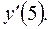
 При значенні аргументу, що дорівнює
При значенні аргументу, що дорівнює  , маємо
, маємо  Знаходимо приріст функції:
Знаходимо приріст функції:
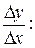
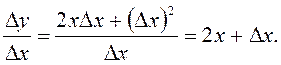
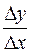 при
при 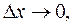 а саме
а саме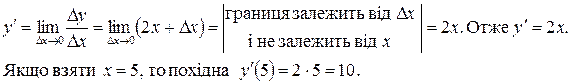
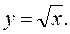
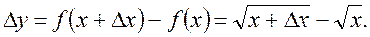

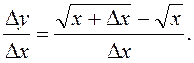 Таким чином,
Таким чином,

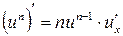
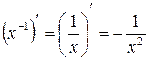



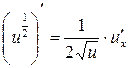

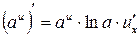
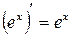
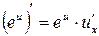
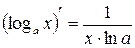


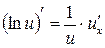
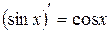
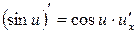

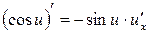

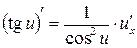

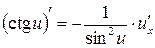
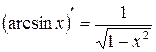
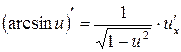
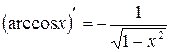





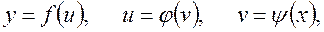 то похідна від складеної функції по аргументу x дорівнює
то похідна від складеної функції по аргументу x дорівнює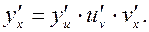 (7)
(7) , де
, де  – кут нахилу дотичної, проведеної до графіка функції у точці з абсцисою x.
– кут нахилу дотичної, проведеної до графіка функції у точці з абсцисою x.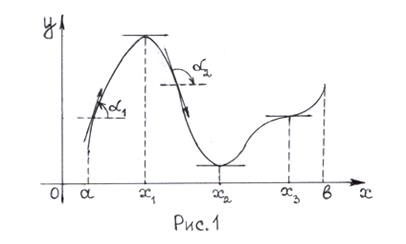 Будемо рухатися вздовж кривої зліва направо. Із рисунка видно, що коли функція зростає на деякому проміжку, то кут нахилу дотичної до кривої гострий, тому
Будемо рухатися вздовж кривої зліва направо. Із рисунка видно, що коли функція зростає на деякому проміжку, то кут нахилу дотичної до кривої гострий, тому 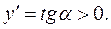 Якщо ж функція спадає, то навпаки, кут нахилу дотичної до кривої буде тупим, а отже
Якщо ж функція спадає, то навпаки, кут нахилу дотичної до кривої буде тупим, а отже  . Постараємося тепер аналітично обґрунтувати наші геометричні спостереження і висновки.
. Постараємося тепер аналітично обґрунтувати наші геометричні спостереження і висновки.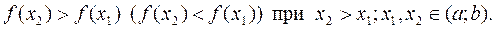
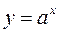 при а>1 є зростаючою на всій числовій осі; при 0< a <1 – спадною на всій числовій осі.
при а>1 є зростаючою на всій числовій осі; при 0< a <1 – спадною на всій числовій осі.

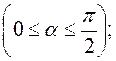 2) дотична до графіка спадної функції – тупий кут (або в окремих точках) горизонтальна
2) дотична до графіка спадної функції – тупий кут (або в окремих точках) горизонтальна 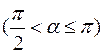 .
.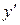


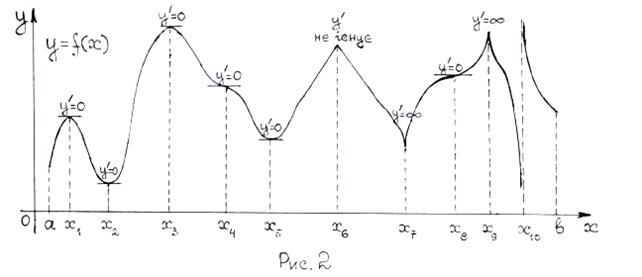 .
.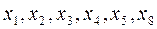 ). В точках, де похідна дорівнює нескінченності, дотична перпендикулярна до осі Ox (на рис. 2 це точки
). В точках, де похідна дорівнює нескінченності, дотична перпендикулярна до осі Ox (на рис. 2 це точки 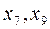 ); їх називають зворотними точками. В точках, де похідна не існує, не існує і дотична (на рис. 2 це точка
); їх називають зворотними точками. В точках, де похідна не існує, не існує і дотична (на рис. 2 це точка 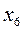 ); їх називають кутовими точками.
); їх називають кутовими точками.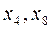 ). Якщо на двох сусідніх інтервалах, розділених стаціонарною точкою, знак похідної
). Якщо на двох сусідніх інтервалах, розділених стаціонарною точкою, знак похідної  однаковий, то ці інтервали складають єдиний інтервал монотонності. На рис. 2 інтервали
однаковий, то ці інтервали складають єдиний інтервал монотонності. На рис. 2 інтервали 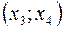 та
та  складають єдиний інтервал спадання функції
складають єдиний інтервал спадання функції 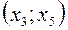 , а інтервали
, а інтервали 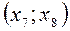 та
та 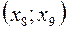 – єдиний інтервал зростання функції
– єдиний інтервал зростання функції 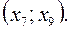
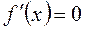 або нескінченності або не існує.
або нескінченності або не існує.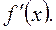
 або не існує.
або не існує.
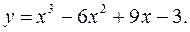
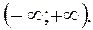 2) Знаходимо похідну:
2) Знаходимо похідну: 
 .
. 4) Наносимо критичні (стаціонарні) точки на область визначення функцій (рис.3).
4) Наносимо критичні (стаціонарні) точки на область визначення функцій (рис.3). Так як похідна
Так як похідна  може змінювати знак тільки при переході через точки, в яких вона перетворюється в нуль або терпить розрив неперервності (в даному випадку точки розриву
може змінювати знак тільки при переході через точки, в яких вона перетворюється в нуль або терпить розрив неперервності (в даному випадку точки розриву 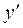 відсутні), то в кожному із інтервалів похідна зберігає знак, тому в кожному із цих інтервалів задана функція монотонна. 5) Встановлюємо знак похідної на кожному інтервалі. Для цього достатньо визначити знак похідної в одній довільній внутрішній точці (пробній точці) кожного інтервалу. Маємо
відсутні), то в кожному із інтервалів похідна зберігає знак, тому в кожному із цих інтервалів задана функція монотонна. 5) Встановлюємо знак похідної на кожному інтервалі. Для цього достатньо визначити знак похідної в одній довільній внутрішній точці (пробній точці) кожного інтервалу. Маємо 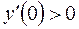 – функція зростає на інтервалі
– функція зростає на інтервалі 
 – функція спадає на інтервалі (1;3);
– функція спадає на інтервалі (1;3); 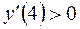 – функція зростає на інтервалі
– функція зростає на інтервалі  .
.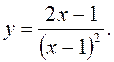
 2)
2) 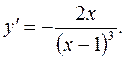 Рекомендуємо переконатися самостійно, що похідна знайдена вірно. 3) Знаходимо критичні точки 1-го роду:
Рекомендуємо переконатися самостійно, що похідна знайдена вірно. 3) Знаходимо критичні точки 1-го роду: 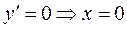 – стаціонарна точка. Інших критичних точок функція не має.
– стаціонарна точка. Інших критичних точок функція не має.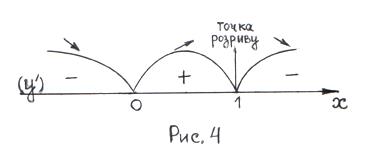 4) Відмічаємо критичні точки на ОВФ (дивись рис. 4). Інтервали монотонності:
4) Відмічаємо критичні точки на ОВФ (дивись рис. 4). Інтервали монотонності: 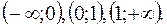
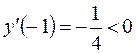 – функція спадає на
– функція спадає на 
 – функція зростає на (0;1);
– функція зростає на (0;1); – функція спадає на
– функція спадає на 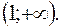
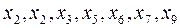 ). Вони відокремлюють область зростання функції від області її спадання або навпаки, тобто при переході через ці точки поведінка функції змінюється. До розгляду поведінки функції в околі такої точки ми зараз і перейдемо.
). Вони відокремлюють область зростання функції від області її спадання або навпаки, тобто при переході через ці точки поведінка функції змінюється. До розгляду поведінки функції в околі такої точки ми зараз і перейдемо. і точка
і точка 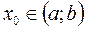 . Введемо наступні означення:
. Введемо наступні означення: якщо значення функції у цій точці більше (менше), ніж її значення в усіх інших точках деякого околу точки
якщо значення функції у цій точці більше (менше), ніж її значення в усіх інших точках деякого околу точки  , тобто
, тобто 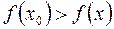
 для всіх x досить близьких до
для всіх x досить близьких до 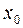 .
.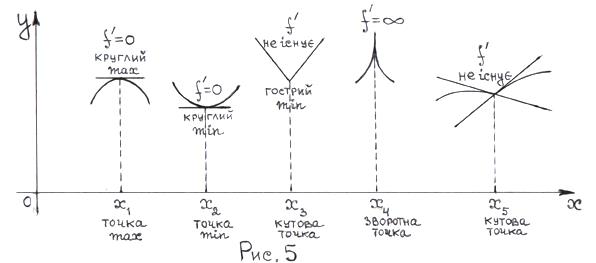
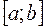 , то вона може досягати екстремуму тільки всередині цього відрізка. Чому? Тому що згідно означення екстремуму функції в точці, ми повинні знати всю інформацію про характер зміни функції в деякому околі, який охоплює точку і який належить ОВФ. Окремі А кінцеві точки a та b охопити такими околами неможливо.
, то вона може досягати екстремуму тільки всередині цього відрізка. Чому? Тому що згідно означення екстремуму функції в точці, ми повинні знати всю інформацію про характер зміни функції в деякому околі, який охоплює точку і який належить ОВФ. Окремі А кінцеві точки a та b охопити такими околами неможливо.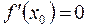 або
або 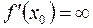 або
або  не існує
не існує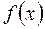 у точці
у точці 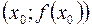 горизонтальна (паралельна осі Ox). Умова
горизонтальна (паралельна осі Ox). Умова  означає, що ця дотична вертикальна (
означає, що ця дотична вертикальна (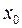 – зворотна точка). Умова
– зворотна точка). Умова 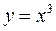 точка x =0 є критичною точкою. Дійсно,
точка x =0 є критичною точкою. Дійсно, 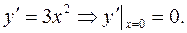
 ,(крім, можливо, самої точки
,(крім, можливо, самої точки  зліва направо похідна функції
зліва направо похідна функції  змінює знак з «+» на «–», то точка
змінює знак з «+» на «–», то точка 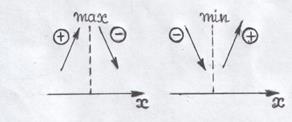 2) якщо ж при такому переході похідна
2) якщо ж при такому переході похідна 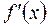 змінює знак з «–» на «+», то точка
змінює знак з «–» на «+», то точка  Повернемося до прикладу 1 п.3.1. Нами були знайдені інтервали монотонності функції
Повернемося до прикладу 1 п.3.1. Нами були знайдені інтервали монотонності функції 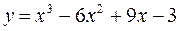 та визначений характер її поведінки на кожному інтервалі (дивись рис,3). Продовжимо дослідження – знайдемо екстремальні точки цієї функції, скориставшись достатньою ознакою екстремуму. 1) Так як при переході через стаціонарну точку
та визначений характер її поведінки на кожному інтервалі (дивись рис,3). Продовжимо дослідження – знайдемо екстремальні точки цієї функції, скориставшись достатньою ознакою екстремуму. 1) Так як при переході через стаціонарну точку  похідна змінює знак з «+» на «–», то згідно першого правила в точці
похідна змінює знак з «+» на «–», то згідно першого правила в точці 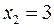 похідна змінює знак з «–» на «+», то в точці
похідна змінює знак з «–» на «+», то в точці 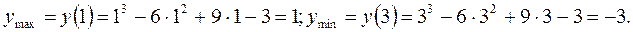 Тоді А(1;1) та В(3;-3) – це точки на графіку функції, де вона досягає максимуму та мінімуму відповідно. 3) Результати дослідження поведінки функції, схематично зображені на рис. 6, дають можливість легко побудувати ескіз графіка функції. Що ми й зробимо. Дамо декілька порад щодо побудови наближеного графічного зображення даної функції. Спочатку наносимо на вісь Ox, яка є областю визначення нашої функції, характерні точки. В даному випадку обмежимося тільки екстремальними точками
Тоді А(1;1) та В(3;-3) – це точки на графіку функції, де вона досягає максимуму та мінімуму відповідно. 3) Результати дослідження поведінки функції, схематично зображені на рис. 6, дають можливість легко побудувати ескіз графіка функції. Що ми й зробимо. Дамо декілька порад щодо побудови наближеного графічного зображення даної функції. Спочатку наносимо на вісь Ox, яка є областю визначення нашої функції, характерні точки. В даному випадку обмежимося тільки екстремальними точками 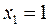 та
та 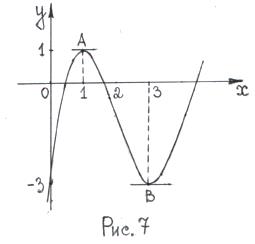 Правило дослідження функції f(x) на монотонність та екстремум:
Правило дослідження функції f(x) на монотонність та екстремум: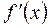

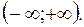 2) Знаходимо похідну
2) Знаходимо похідну 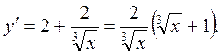
 а)
а) 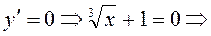
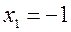 – стаціонарна точка;
– стаціонарна точка; б)
б) 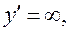 коли знаменник дробу дорівнює нулю, тобто коли
коли знаменник дробу дорівнює нулю, тобто коли 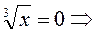
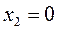 – критична точка. Зазначимо, що в цій точці похідна терпить розрив, а сама функція визначена і неперервна. Інших критичних точок немає. 4) Відмічаємо критичні точки на ОВФ (
– критична точка. Зазначимо, що в цій точці похідна терпить розрив, а сама функція визначена і неперервна. Інших критичних точок немає. 4) Відмічаємо критичні точки на ОВФ ( дивись рис. 8) Інтервали монотонності:
дивись рис. 8) Інтервали монотонності: 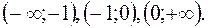
 – функція зростає на
– функція зростає на 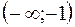 ;
; – функція спадає на (–1;0);
– функція спадає на (–1;0);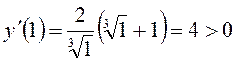

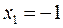 похідна змінює знак з «+» на «–», отже точка
похідна змінює знак з «+» на «–», отже точка 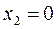 похідна змінює знак з
похідна змінює знак з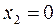 – це точка гострого мінімуму (дивись рис. 8). 7) Обчислимо екстремальні значення функції:
– це точка гострого мінімуму (дивись рис. 8). 7) Обчислимо екстремальні значення функції: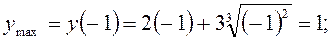
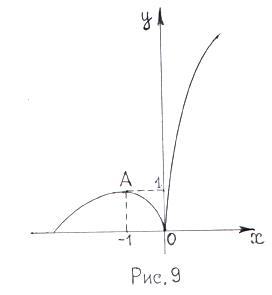

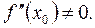 Тоді
Тоді то
то 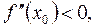 то
то  у точці
у точці 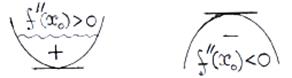

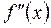 .
.
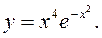
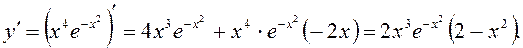
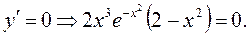
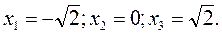


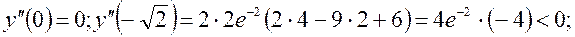
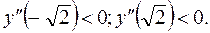 Тому, згідно з другого правилом у стаціонарних точках
Тому, згідно з другого правилом у стаціонарних точках 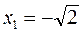 та
та 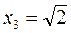 функція досягає максимуму.
функція досягає максимуму.
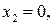 то нічого конкретного поки сказати неможливо. Для її дослідження потрібно скористатися першою достатньою ознакою. Доходимо висновку, що друге правило застосовне для вужчого класу функцій, ніж перше.
то нічого конкретного поки сказати неможливо. Для її дослідження потрібно скористатися першою достатньою ознакою. Доходимо висновку, що друге правило застосовне для вужчого класу функцій, ніж перше.


