

Мы поможем в написании ваших работ!
ЗНАЕТЕ ЛИ ВЫ?
|
Тема 3. Тестирование общей физической подготовленности занимающихся физкультурой и спортом
Похожие статьи вашей тематики
Тема: Тестирование общей физической подготовленности занимающихся физкультурой и спортом
Цель: на примере тестирования ОФП по 10 тестам закрепить требования стандартизации тестов и активно исполнить роль экспериментатора и исследуемого.
Теоретические сведения
Слово тест в переводе с английского означает "проба" или "испытание". Впервые этот термин появился в научной литературе в конце прошлого века, а широкое распространение получил после опубликования в 1912 г. американским психологом Э.Торндайком работы по применению теории тестов в педагогике.
В спортивной метрологии тестом называют измерение или испытание, проводимое с целью определения состояния или характеристик спортсмена, которое удовлетворяет следующим специальным метрологическим требованиям:
1. Стандартизованность — соблюдение комплекса мер, правил и требований к тесту, т.е. процедура и условия проведения тестов должны быть одинаковыми во всех случаях использования их. Все тесты стараются унифицировать и стандартизировать.
2. Информативность — это свойство теста отражать то качество системы (например, спортсмена), для которого он используется.
3. Надежность теста — степень совпадения результатов при повторном тестировании одних и тех же людей в одинаковых условиях.
4. Наличие системы оценок.
Ход работы
1. Постановка задачи тестирования. Каждый из студентов должен протестироваться по всем 10-ти предлагаемым тестам и свои результаты записать в свою строку групповой таблицы 4.
2. Тестирование каждого исследуемого производится в следующей последовательности:
Тест 1. Вес измеряется на медицинских весах, которые предварительно уравновешиваются на нуле с помощью подвижных балансов. Величина веса (Р) отсчитывается на шкале с точностью до 1 кг и записывается в столбец 3 таблицы.
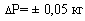
Тест 2. Рост измеряется с помощью ростомера. Величина роста (H) отсчитывается по сантиметровой шкале с точностью до 1 см и записывается в столбец 4 таблицы.
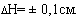
Тест 3. Индекс Кетле, характеризующий весо-ростовое соотношение, рассчитывается путем деления веса исследуемого в граммах на рост в сантиметрах. Результат записывается в столбец 5.
Тест 4. Пальпаторно в области лучевой или сонной артерии измеряется частота сердечных сокращений в состоянии относительного покоя (ЧССп) за 1 мин и записывается в столбец 6. Затем испытуемый выполняет 30 полных приседаний (темп — одно приседание в секунду) и сразу после нагрузки измеряется ЧСС за 10 с. После 2-х минут отдыха измеряется ЧСС восстановления за 10 с. Затем результаты пересчитываются за 1 мин и записываются в столбцы 7 и 8.
Тест 5. Расчет индекса Руфье производится по формуле:
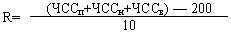
Тест 6. Становым динамометром измеряется с точностью до ± 5 кГ максимальная сила мышц-разгибателей спины. При выполнении теста руки и ноги должны быть прямые, ручка динамометра — на уровне коленных суставов. Результат записывается в столбец 10.
Тест 7. Измерение уровня гибкости проводится в линейных единицах по методу Н.Г.Озолина в собственной модификации с помощью специально сконструированного прибора. Исследуемый садится на мат, упираясь ногами в перекладину прибора, руками, вытянутыми вперед, захватывает ручку измерительной ленты; спина и руки образуют угол 90о. Фиксируется длина ленты, вытянутой из прибора. При наклоне исследуемого вперед до упора вновь измеряется длина ленты. Расчет показателя гибкости ведется в условных единицах по формуле:
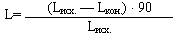
| где: Lисх. — исходный показатель длины ленты, вытянутой из прибора;
| | Lкон. — конечный показатель длины ленты.
|
Результаты заносятся в столбец 11.
Тест 8. Перед исследуемым на столе лежит доска, разделенная на 4 квадрата (20х20 см). Исследуемый касается квадратов кистью руки в следующей последовательности: левый верхний — правый нижний — левый нижний — правый верхний (для правшей). Учитывается число правильно выполненных циклов движения за 10 с. Результаты заносятся в столбец 12.
Тест 9. Для определения уровня быстроты используется измерительный комплекс, состоящий из контактной платформы, интерфейса, компьютера и монитора. Исследуемый выполняет бег на месте с высоким подниманием бедра в течение 10 с (теппинг-тест). Сразу по окончании бега на экране монитора строится гистограмма параметров опорных и безопорных фаз, выводятся данные о количестве шаговых циклов, средние значения времени опоры и времени полета в мс. Основным критерием оценки уровня развития быстроты служит время опоры, так как этот параметр более стабилен и информативен. Результаты заносятся в столбец 13.
Тест 10. Для оценки скоростно-силовых качеств используется модификация теста Абалакова с применением измерительного комплекса. По команде с монитора исследуемый выполняет на контактной платформе прыжок вверх с места со взмахом руками. После приземления в реальном времени рассчитывается время полета в мс и высота прыжка в см. Критерием оценки результатов данного теста служит время полета, так как между данным показателем и высотой прыжка выявлена прямая функциональная зависимость. Результаты заносятся в столбец 14.
3. В конце занятия каждый исследуемый диктует свои результаты всей группе. Таким образом, каждый студент заполняет таблицу результатов ОФП по всей подгруппе, которую в дальнейшем будет использовать в качестве экспериментального материала для освоения методов обработки результатов тестирования и для выполнения индивидуальных заданий по РГР.
ТЕМА 4. МАТЕМАТИЧЕСКАЯ СТАТИСТИКА, ЕЕ ОСНОВНЫЕ ПОНЯТИЯ И ПРИЛОЖЕНИЕ К ФИЗИЧЕСКОЙ КУЛЬТУРЕ И СПОРТУ
1. Возникновение и развитие математической статистики
Издавна в каждом государстве соответствующими органами власти собирались сведения о числе жителей по полу, возрасту, занятости в различных сферах труда, наличии различных воинов, вооружения, денежных средств, орудий труда, средств производства и т.д. Все эти и подобные им данные называются статистическими. С развитием государства и международных отношений возникла необходимость анализа статистических данных, их прогнозирование, обработка, оценка достоверности основанных на их анализе выводов и т.п. К решению таких задач стали привлекаться математики. Таким образом, в математике сформировалась новая область — математическая статистика, изучающая общие закономерности статистических данных или явлений и взаимосвязи между ними.
Сфера применения математической статистики распространилась во многие, особенно экспериментальные, науки. Так появились экономическая статистика, медицинская статистика, биологическая статистика, статистическая физика и т.д. С появлением быстродействующих ЭВМ возможность применения математической статистики в различных сферах деятельности человека постоянно возрастает. Расширяется ее приложение и к области физической культуры и спорта. В связи с этим основные понятия, положения и некоторые методы математической статистики рассматриваются в курсе “Спортивная метрология”. Остановимся на некоторых основных понятиях математической статистики.
2. Статистические данные
В настоящее время под термином "статистические данные" понимают все собранные сведения, которые в дальнейшем подвергаются статистической обработке. В различной литературе их еще называют: переменные, варианты, величины, даты и т.д. Все статистические данные можно разделить на: качественные, труднодоступные для измерения (имеется, не имеется; больше, меньше; сильно, слабо; красный, черный; мужской, женский и т.д.), и количественные, которые можно измерить и представить в виде числа общих мер (2 кг, 3 м, 10 раз, 15 с и т.д.); точные, величина или качество которых не вызывают сомнений (в группе 6 человек, 5 столов, деревянный, металлический, мужской, женский и т.д.), и приближенные, величина или качество которых вызывает сомнение (все измерения: рост 170 см, вес 56 кг, результат бега на 100 м - 10,3 с и т.д.; близкие понятия — синий, голубой, мокрый, влажный и т.д.); определенные (детерминированные), причины появления, не появления или изменения которых известны (2 + 3 = 5, подброшенный вверх камень обязательно будет иметь вертикальную скорость, равную 0 и т.д.), и случайные, которые могут появляться и не появляться или не все причины изменения которых известны (пойдет дождь или нет, родится девочка или мальчик, команда выиграет или нет, в беге на 100 м — 12,2 с, принятая нагрузка вредна или нет). В большинстве случаев в физической культуре и спорте мы имеем дело с приближенными случайными данными.
3. Статистические признаки, совокупности
Общее свойство, присущее нескольким статистическим данным, называют их статистическим признаком. Например, рост игроков команды, результат бега на 100 м, принадлежность к виду спорта, частота сердечных сокращений и т.д.
Статистической совокупностью называют несколько статистических данных, объединенных в группу хотя бы одним статистическим признаком. Например, 7.50, 7.30, 7.21, 7.77 — результаты прыжка в длину в метрах у одного спортсмена; 10, 12, 15, 11, 11 — результаты подтягивания на перекладине пяти студентов и т.д. Число данных в статистической совокупности называют ее объемом и обозначают n. Различают следующие совокупности:
бесконечные — n  (масса планет Вселенной, число молекул и т.д.); (масса планет Вселенной, число молекул и т.д.);
конечные — n - конечное число;
большие — n > 30;
малые — n  30; 30;
генеральные — содержащие все данные, обусловленные постановкой задачи;
выборочные — части генеральных совокупностей.
Например, пусть рост студентов 17-22 лет в РФ — генеральная совокупность, тогда рост студентов КГАФК, всех студентов города Краснодара или студентов II курса — выборки.
4. Кривая нормального распределения
При анализе распределения результатов измерений всегда делают предположение о том распределении, которое имела бы выборка, если бы число измерений было очень большим. Такое распределение (очень большой выборки) называют распределением генеральной совокупности или теоретическим, а распределение экспериментального ряда измерений — эмпирическим.
Теоретическое распределение большинства результатов измерений описывается формулой нормального распределения, которая впервые была найдена английским математиком Муавром в 1733 г.:

Это математическое выражение распределения позволяет получить в виде графика кривую нормального распределения (рис.3), которая симметрична относительно центра группирования (обычно это значение, моды или медианы). Эта кривая может быть получена из полигона распределения при бесконечно большом числе наблюдений и интервалов. Заштрихованная область графика на рисунке 3 отражает процент результатов измерений, находящихся между значениями х1 и х2.

Рис. 3. Кривая нормального распределения.
Введя обозначение  , которое называется нормированным или стандартизованным отклонением, получают выражение для нормированного распределения: , которое называется нормированным или стандартизованным отклонением, получают выражение для нормированного распределения:
На рисунке 4 представлен график этого выражения. Он примечателен тем, что для него =0 и s =1 (результат нормировки). Вся площадь, заключенная под кривой, равна 1, т.е. она отражает все 100% результатов измерений. Для теории педагогических оценок и особенно для построения шкал представляет интерес процент результатов, лежащих в различном диапазоне варьирования, или колеблемости.
function PlayMyFlash(cmd){ Norm_.SetVariable("Counter", cmd); Norm_.GotoFrame(2); Norm_.Play(); } 
1!!! 1,96!!! 2!!! 2,58!!! 3!!! 3,29!!!

Рис.4. Кривая нормированного распределения с процентным выражением распределений относительных и накопленных частностей:
под первой осью абсцисс — среднее квадратическое отклонение;
под второй (нижней) — накопленный процент результатов.
Для оценки варьирования результатов измерений используют следующие соотношения:
± 1,96  (u= ± 1,96) (u= ± 1,96)
| интервал включает
| 95%
| всех результатов
| ± 2,58  (u= ± 2,58) (u= ± 2,58)
|
| 99%
|
| ± 3,29  (u= ± 3,29) (u= ± 3,29)
|
| 99,9%
|
| ± 1  (u= ±1) (u= ±1)
|
| 68,27%
|
| ± 2  (u= ±2) (u= ±2)
|
| 95,45%
|
| ± 3  (u= ±3) (u= ±3)
|
| 99,73%
|
|
Другими словами, отклонения, большего, чем  , от следует ожидать примерно в одном случае из трех; отклонения, большего, чем 2 , от следует ожидать примерно в одном случае из трех; отклонения, большего, чем 2  , — в четырех-пяти случаях из 100, отклонения, большего, чем 3 , — в четырех-пяти случаях из 100, отклонения, большего, чем 3  , — в трех из 1000. Последнее соотношение для нормального распределения называют "правилом трех сигм" и используют при исключении сильно отклоняющихся "ошибочных" результатов измерений. , — в трех из 1000. Последнее соотношение для нормального распределения называют "правилом трех сигм" и используют при исключении сильно отклоняющихся "ошибочных" результатов измерений.
5. Виды представления статистических данных
После того, как определена выборка и стали известны ее статистические данные (варианты, даты, элементы и т.д.), возникает необходимость представить эти данные в удобном для решения задачи виде. На практике используют много различных видов представления статистических данных. Наиболее часто употребляют следующие:
а) текстовый вид;
б) табличный вид;
в) вариационный ряд;
г) графический вид.
Если при статистической обработке совокупности безразлично в какой последовательности записывать данные, то бывает удобным расположить эти данные (варианты) в соответствии с их значением либо по возрастанию xi ~ 2, 3, 3, 5, 5, 6, 6, 6, 6, 7 (неубывающая совокупность), либо по убыванию xi ~ 7, 6, 6, 6, 6, 5, 5, 3, 3, 3, 2 (невозростающая совокупность). Этот процесс называется ранжированием. А место каждой варианты в ранжированном ряду называется рангом.
Тема: Графическое изображение вариационных рядов
Цель: научиться строить графики (гистограмму и полигон) распределения частот в вариационном ряду и делать по ним выводы об однородности группы по заданному признаку.
Теоретические сведения
Анализ вариационных рядов упрощается при графическом представлении. Рассмотрим основные графики вариационного ряда.
1. Полигон распределения (рис. 5-I). На графике ѕ это кривая, отражающая по оси абсцисс (Х) средние значения классов, а по оси ординат (Y) ѕ частоту накопления величин в каждом классе.
2. Гистограмма распределения (рис. 5 -II). График, выполненный в прямоугольной системе координат и отражающий по оси ординат (Y) частоту накопления величин в классе, а по оси абсцисс (Х) - границы классов.
Графическое представление результатов измерений не только существенно облегчает анализ и выявление скрытых закономерностей, но и позволяет правильно выбрать последующие статистические характеристики и методы.
ПРИМЕР 4.1.
Построить графики вариационного ряда 20 исследуемых по показателям результатов тестирования прыжка в высоту, если данные выборки таковы:
xi, см ~ 185, 170, 190, 170, 190, 178, 188, 175, 192, 178, 176, 180, 185, 176, 180, 192, 190, 190, 192, 194.
Решение:
1. Производим ранжирование вариационного ряда в порядке неубывания:
xi, см ~ 170,170, 174, 176, 176, 178, 178, 180, 180, 185, 185, 188, 190, 190, 190, 190, 192, 192, 192, 194.
2. Определяем минимальное и максимальное значение вариант и рассчитываем размах вариационного ряда по формуле:
R=Xmax — Xmin (1)
R=194-170=24 см
3. Рассчитываем число классов по формуле Стерджеса:
 (2) (2)
N=1+3,31 Ч 1,301=5,30631  5 5
4. Рассчитываем интервал каждого класса по формуле:
 (3) (3)
5. Составляем таблицу границ классов.
| № класса
| Граница класса
| Среднее значение класса
| Частота класса
| Накопленная частота класса
| | 1.
| Xmin  хi < Xmin+k 170см хi < Xmin+k 170см 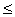 хi < 174,8см хi < 174,8см
| 172,4 см
|
|
| | 2.
| Xmin +k  хi < Xmin+2k 174,8см хi < Xmin+2k 174,8см  хi < 179,6см хi < 179,6см
| 177,2 см
|
|
| | 3.
| Xmin +2k  хi < Xmin+3k 179,6см хi < Xmin+3k 179,6см  хi < 184,4см хi < 184,4см
| 182 см
|
|
| | 4.
| Xmin +3k  хi < Xmin+4k 184,4см хi < Xmin+4k 184,4см  хi < 189,2см хi < 189,2см
| 186,8 см
|
|
| | 5.
| Xmin +4k  хi < Xmin+5k 189,2см хi < Xmin+5k 189,2см  хi < 194см хi < 194см
| 191,6 см
|
|
| 7. Рассчитываем среднее значение каждого класса по формуле:

7. Построим графики гистограммы и полигона данного вариационного ряда (рис.5).


Рис.5. Графическое изображение вариационного ряда
8. Сделаем выводы по построенным графикам гистограммы и полигона об однородности выборки по заданному признаку, учитывая следующие моменты:
- если гистограмма и полигон по своему виду близки к виду графика нормального распределения величин, то группа однородна;
- если графики низкие и растянутые, то группа, возможно, однородна, но некомпактна;
- если графики имеют 2 и более вершины, то группа неоднородна по данному признаку, ее необходимо разбить на подгруппы, чтобы с каждой из подгрупп вести занятия по индивидуальному плану.
Вывод: так как на представленных графиках гистограмма и полигон имеют 2 вершины, то группу исследуемых по показателю прыжка в высоту можно считать неоднородной.
Ход работы
ЗАДАЧА 1.
Построить графики вариационного ряда результатов тестирования 10 исследуемых в показателе _________________________________, если данные выборки таковы:
xi ~
Решение:
1. Проранжировать данный вариационный ряд в порядке неубывания:
xi ~
2. Рассчитать размах вариационного ряда по формуле:
R=Xmax — Xmin
R=
3. Определить число классов выборки по формуле Стерджеса:
N=1+3,31 * lgn
N=
4. Определить интервал класса по формуле:

k=
5. Составить таблицу границ классов:
| № класса
| Граница класса
| Среднее значение класса
| Частота класса
| Накопленная частота класса
| | 1.
| 
| 
| 
| 
| | 2.
| 
| 
| 
| 
| | 3.
| 
| 
| 
| 
| | 4.
| 
| 
| 
| 
| | 5.
| 
| 
| 
| 
| 6. Построить графики гистограммы и полигона данного вариационного ряда:

Вывод:
Контрольные вопросы
1. Что называется вариационным рядом?
2. Что такое ранжирование?
3. Что такое ранг?
4. Основные характеристики вариационного ряда.
5. Графическое изображение вариационных рядов, цель построения графиков.
|



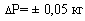
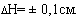
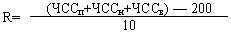
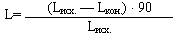
 (масса планет Вселенной, число молекул и т.д.);
(масса планет Вселенной, число молекул и т.д.); 30;
30;

 , которое называется нормированным или стандартизованным отклонением, получают выражение для нормированного распределения:
, которое называется нормированным или стандартизованным отклонением, получают выражение для нормированного распределения:

 (u= ± 1,96)
(u= ± 1,96)
 , от следует ожидать примерно в одном случае из трех; отклонения, большего, чем 2
, от следует ожидать примерно в одном случае из трех; отклонения, большего, чем 2  (2)
(2) 5
5 (3)
(3) хi < Xmin+k 170см
хi < Xmin+k 170см  хi < 174,8см
хi < 174,8см








