
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Электропроводность диэлектриков. Основные параметры.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Токи сквозной электропроводности связаны с наличием в диэлектриках небольшого количества свободных зарядов и инжекцией их из электродов. Проводимость диэлектрика при постоянном напряжении определяется по сквозному току, который сопровождается выделением и нейтрализацией зарядов на электродах. При определении проводимости диэлектриков на постоянном напряжении следует выдерживать их в электрическом поле до полного прекращения протекания токов смещения. При переменном напряжении активная проводимость определяется не только сквозным током, но и активными составляющими токов смещения. Электропроводность диэлектриков в большинстве случаев ионная, реже –электронная. У твердых диэлектриков различают объемную и поверхностную электропроводности. Для их сравнительной оценки у разных материалов используют удельное объемное r и удельное поверхностное rs сопротивления. Удельное объемное сопротивление r численно равно сопротивлению куба с ребром в 1 м, мысленно выделенного из материала, если ток проходит через две противоположные грани этого куба и имеет размерность [ Ом×м ]; 1 Ом×м = 100 Ом×см. В случае плоского образца материала при однородном поле r рассчитывают по формуле:
Где R – объемное сопротивление, Ом; S – площадь электрода, м2; h – толщина образца, м. Удельное поверхностное сопротивление rs численно равно сопротивлению квадрата (любых размеров), мысленно выделенного на поверхности материала, если ток проходит через две противоположные стороны этого квадрата. Размерность rs [ Ом ]. Удельное поверхностное сопротивление определяется по формуле:
Где Rs – поверхностное сопротивление образца материала между параллельно поставленными электродами шириной d, отстоящими друг от друга на расстоянии r. По удельному объемному сопротивлению можно определить удельную объемную проводимость:
и соответственно удельную поверхностную проводимость:
Электропроводность диэлектриков зависит от их агрегатного состояния, а также от влажности и температуры окружающей среды. Сопротивление диэлектрика (сопротивление изоляции) 𝑅из, заключенного между двумя пластинами, к которым приложено напряжение 𝑈, вычисляется по формуле: 𝑅из =𝑈𝐼ут −Σ︀𝐼пол, (3.18) где Σ︀𝐼пол = 𝐼абс — сумма токов, вызванных замедленными меха- низмами поляризации.
Полная проводимость твердого диэлектрика есть сумма объемной и поверхностной проводимостей: 1/𝑅из=1/𝑅+1/𝑅S. (3.19) Величина, характеризующая время, в течение которого на- пряжение на обкладках конденсатора, отключенного от питания, уменьшается вследствие разрядки в 𝑒раз, называется постоянной времени 𝜏0: 𝜏0 = 𝑅из 𝐶 = 8,85 ・ 10−12 𝜌 𝜀. Диэлектрические потери В инженерной практике чаще всего для характеристики рассеивать энергию в электрическом поле используют угол диэлектрических потерь. А так же тангенс этого угла. Основные понятия Диэлектрическими потерями называют электрическую мощность, затрачиваемую на нагрев диэлектрика, находящегося в электрическом поле. Рассмотрим эквивалентную схему конденсатора с диэлектриком, обладающим потерями. Она построена путем замены конденсатора с потерями на идеальный конденсатором с параллельно или последовательно включенным активным сопротивлением (рис. 3.5).
Рис. 3.5. Параллельная (а) и последовательная (б) эквивалентные схемы диэлектрика с потерями и векторные диаграммы для них Обе схемы эквивалентны друг другу, если при равенстве полных сопротивлений Z1=Z2=Z равны соответственно их активные и реактивные составляющие. Это условие будет соблюдено, если углы сдвига тока относительно напряжения равны и значения активной мощности одинаковы. Для параллельной схемы:
Где: Ia – активная составляющая тока; Ic – реактивная составляющая тока. Тогда из векторной диаграммы для параллельной схемы:
Мощность, рассеиваемая в диэлектрике, для данной схемы равна:
Для последовательной схемы:
где Ua – активная составляющая напряжения; Uc – реактивная составляющая напряжения. Тогда из векторной диаграммы для последовательной схемы:
Мощность, рассеиваемая в диэлектрике, для данной схемы равна:
где Из приведенных выражений для параллельной и последовательной схем можно найти соотношения между Ср и Сs, а также между R и r:
Таким образом, углом диэлектрических потерь d называют угол, дополняющий до 90° угол сдвига фаз j между током и напряжением в емкостной цепи. В случае идеального диэлектрика вектор тока в цепи опережает вектор напряжения на угол 90°, при этом угол d равен нулю. Чем больше рассеиваемая в диэлектрике мощность, тем меньше угол сдвига фаз j и тем больше угол диэлектрических потерь d и его функция tgd. Для доброкачественных диэлектриков можно пренебречь значением tg2d по сравнению с единицей и считать Cp»Cs=C. Тогда выражения для мощности, как у параллельной, так и у последовательной схем будут одинаковы:
где Ра выражено в Вт; U – в В; w - в с-1; C – в Ф. Как видно, тангенс угла диэлектрических потерь непосредственно входит в формулу для рассеиваемой в диэлектрике мощности, поэтому практически наиболее часто пользуются этой характеристикой. Диэлектрические потери по их физической природе можно разделить на четыре основных вида: потери на электропроводность, релаксационные потери, ионизационные потери, резонансные потери. Пробой диэлектриков Минимальное напряжение U пр, приводящее к образованию в диэлектрике электропроводящего канала, называется пробивным напряжением. Электрическая прочность, то есть способность диэлектрика сохранять высокое удельное сопротивление, характеризуется напряженностью электрического поля при пробое изоляции в однородном электрическом поле E пр = U пр / d, В/м, (3.28) где U пр – пробивное напряжение, В; d – толщина диэлектрика, м. Электрическая прочность не является фундаментальным параметром материала. Различают следующие механизмы пробоя диэлектриков: - электрический, - электротепловой, - электрохимический, - поверхностный, - ионизационный. В режиме, близком к электрическому пробою, зависимость удельной проводимости от напряженности поля описывается эмпирической формулой Пуля γ = γ0 exp(β1E), (3.29) а в некоторых случаях формулой Френкеля γ = γ0 exp(β2 E), (3.30) где γ0 – удельная проводимость в области независимости γ от E, β1, β2 – коэффициенты, характеризующие материал. КОНДЕНСАТОРЫ Электроемкость (С) любого конденсатора называется физическая величина, численно равная отношению заряда (G) одной из обкладок конденсатора к разности потенциалов (U) между обкладками
С= G/ U (3.31) Электроемкость плоского конденсатора в СИ выражается формулой:
С= ε ε0 S/d (3.32) Где: - S – площадь одной из обкладок конденсатора; - d –. расстояние между обкладками При параллельном включении конденсаторов их электроемкость складывается
С=С1+ С2 + С3 ….(3.33) При последовательном включении конденсаторов их электроемкость рассчитывается по формуле 1/С=1/С1 +1/C2 …….(3.34) Энергия (W) заряженного конденсатора в СИ выражается формулой W = С U2/2……. (3.35) Если к электродам, между которыми расположен какой либо диэлектрик толщиной h, приложить напряжение U, то в диэлектрике возникает электрическое поле E с напряженностью равной U/ h (В/м) E= U/ h (3.36) Распределение напряженности электрического поля в двухслойном диэлектрике описывается выражением: ε 1*Ε1= ε 2*Ε2 (3.37) где: - ε 1, ε 2 – диэлектрические проницаемости материал слоев; - Ε1, Ε2–. напряженность электрического поля в данных диэлектриках.
|
||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 798; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.251.204 (0.006 с.) |

 , Ом*м (3.14)
, Ом*м (3.14) , Ом (3.15)
, Ом (3.15)
 (3.16)
(3.16)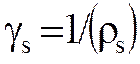 (3.17)
(3.17)

 , (3.20)
, (3.20) (3.21)
(3.21)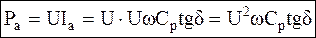 (3.22)
(3.22)
 (3.23)
(3.23) (3.24)
(3.24) (3.25)
(3.25) - реактивная составляющая сопротивления цепи.
- реактивная составляющая сопротивления цепи. (3.26)
(3.26) (3.27)
(3.27) (3.28)
(3.28)


