
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Регрессионный анализ взаимосвязи признаков
1. Выбор аналитической формы связи
Для того, чтобы полностью абстрагироваться (отвлечься) от влияния на Y всех иных (кроме X) факторов и установить подлинную закономерность взаимосвязи признаков X и Y, в статистике прибегают к выравниванию эмпирической ломаной линии связи по некоторой плавной, «сглаженной» кривой, около которой группируются или к которой тяготеют точки (xi,
Линию, сглаживающую эмпирическую ломаную линию связи, называют теоретической линией регрессии Y на X или просто линией регрессии. Эта линия отражает теоретическую форму связи признаков X и Y, т.е. закономерность изменения средних значений признака Y в зависимости от изменения фактора X при условии полного взаимопоглощения всех прочих случайных по отношению к фактору X причин. Иначе говоря, теоретическая линия регрессии определяет основную тенденцию взаимосвязи признаков X и Y.
Уравнение, описывающее математически теоретическую линию регрессии, называют уравнением парной регрессии:
В уравнении (17) переменная
Для парной корреляционной связи
Вид функции
Выбор функции
Наиболее простой регрессионной моделью однофакторой корреляционной связи является линейная модель (18), графически изображаемая прямой линией. Модель отражает линейную взаимосвязь признаков XиY, когда с возрастанием значений Х происходит непрерывное, более или менее равномерное возрастание или убывание средних значений Y (рис.3).
Все прочие модели (17) отражают тот или иной вид нелинейной взаимосвязи признаков, когда изменение средних значений Y в зависимости от X происходит неравномерно (с ускорением, замедлением или изменением направления связи). В этих случаях сглаживающие теоретические линии регрессии представляют собой соответствующие нелинейные кривые – гиперболы, параболы 2-го порядка (как на рис.4) и др.
2. Расчет числовые значения параметров выбранной математической функции связи Разброс фактических значений yi вокруг теоретических значений Оценить отклонения расчётных значений
Следовательно, при построении регрессионной модели численные значения коэффициентов ak выбранного типового уравнения регрессии (17) необходимо подбирать так, чтобы обеспечить наименьшие возможные остатки
Для этой цели используется метод наименьших квадратов (МНК), который позволяет рассчитать параметры ak выбранного типового уравнения регрессии таким образом, чтобы теоретическая линия регрессии была бы в среднем наименее удалена от всех точек (xi, yi) по сравнению с любой другой теоретической линией регрессии, отвечающей выбранному типу функции связи (17).
Согласно МНК, задача поиска значений параметров ak, минимизирующих сумму погрешностей, имеет вид:
и решается как задача на экстремум – путем приравнивания нулю первых частных производных функции S по каждому искомому параметру ak уравнения регрессии. Это приводит к системе уравнений, называемой нормальной, решение которой даёт численные значения параметров ak, минимизирующие функцию S.
При линейной зависимости
Для нахождения значений параметров а0, а1, при которых функция двух переменных S может достигнуть минимума, решают задачу на экстремум, приравнивая к нулю частные производные S по а0, а1. Тем самым получают систему 2-х уравнений с двумя неизвестными а0, а1:
Сократив каждое уравнение на –2, раскрыв скобки и перенеся члены с х в одну строку, а с y – в другую, для определения а0, а1 получают систему:
Эта система называется системой нормальных уравнений МНК для линейного уравнения регрессии
Все суммы, необходимые для конкретизации нормальных уравнений, определяют по исходным эмпирическим данным (xi, yi). Решая полученную систему, находят искомые параметры а0, а1 – коэффициенты линейного уравнения регрессии.
Расчёт коэффициента может быть выполнен по формулам:
Путём соответствующих преобразований они могут быть представлены в следующем виде:
Если зависимость между х и у выражена в виде параболы второго порядка
то параметры находят методом наименьших квадратов, решив систему нормальных уравнений
При гиперболической корреляции - обратной зависимости
система нормальных уравнений для расчета параметров уравнения регрессии имеет вид:
Зависимость между х и у также может выражаться уравнением параболы более высокого порядка,логарифмической, степенной или другими функциями. Для каждой из них имеется соответствующая система нормальных уравнений.
ПРИМЕР ПОСТРОЕНИЯ ЛИНЕЙНОГО УРАВНЕНИЯ РЕГРЕСИИ
Имеются следующие условные данные о размере страховой суммы и страховых выплат на автотранспортные средства одной из страховых компаний Таблица 7 Расчётная таблица для определения параметровуравнения регрессии
Решение. Система нормальных уравнений (22)
для данных таблицы принимает вид:
Решение системы методом исключений или по формулам (23), (24) дает:
Тогда модель связи в виде линейного уравнения регрессий имеет вид:
Расчётные значения страховых выплат Наблюдаются отклонения между фактическими и теоретическими значениями yi. Однако суммарные значения совпадают (26,65=25,650). Это свидетельствует, что из всех возможных линейных моделей построенная модель является наилучшей. Это объясняется тем, что она получена методом наименьших квадратов (МНК) путём решения задачи на экстремум.
Коэффициент a1 при факторе Х называется коэффициентом регрессии. Величина коэффициента регрессии a1 показывает, на сколько в среднем изменяется значения результативного признака Y при изменении фактора Х на единицу его измерения. Знак при a1 показывает направление этого изменения. В примере единицей измерения X и Y является 1000 $. Следовательно, коэффициент регрессии
При изучении многофакторных корреляционных связей методология их моделирования уравнениями регрессии аналогична рассмотренной.
Уравнения многофакторной регрессии имеют вид:
и позволяют приближенно оценить меру влияния на результативный признак Y каждого из включенных в модель факторов X. Наиболее простыми для построения и анализа являются многофакторные линейные модели, которые содержат независимые переменные только первой степени:
Методом наименьших квадратов для нее получна систему нормальных уравнений:
Параметры уравнения множественной регрессии С изменением факторного признака ak, на единицу его измерения (при неизменном значении других факторов) результативный признак Y изменяется в среднем на величину параметра ak.
Необходимо отметить, что параметры связи ak, в силу их расчета по МНК, являются усредненными по всей совокупности наблюдений (xi, yi). Они отражают взаимосвязь признаков X и Y только в общем итоге, по всей совокупности в целом (для каждой индивидуальной пары (xi, yi) значения ak остаются неизвестными.
3. Анализ качества построенной модели Этот этап заключается в анализе адекватности и практической пригодности построенной регрессионной модели. Анализ качества регрессионной модели ставит задачу – определить, насколько построенная теоретическая модель взаимосвязи признаков отражает фактическую зависимость между этими признаками. Анализ выполняется в 3 этапа:
1) измерение тесноты связи признаков в уравнении регрессии; 2) определение по величине показателей тесноты связи практической пригодности построенной модели связи; 3) проверка статистической значимости показателей тесноты связи.
Этап 1. Для построенной регрессионной модели измерение тесноты связи признаков X и Y осуществляется на основе следующих показателей: R2 - коэффициент (или индекс) детерминации, показывающий, какая часть общей вариации расчетных (теоретических) значений признака Y объясняется вариацией фактора X; R – индекс корреляции (называемый также теоретическим корреляционным отношением и обозначаемый r – линейный коэффициент корреляции, используемый для измерения тесноты связи признаков в регрессионной модели в случае линейной функции связи f(x).
Расчет этих показателей определяется следующими формулами:
где a1 – коэффициент регрессии в регрессионной модели связи. Используя соотношения для вычисления соответствующих дисперсий, а также известное из математической статистики правило сложения дисперсий
для расчета показателей R2 и R применяют формулы:
В многофакторном корреляционном анализе для характеристики тесноты связи между изучаемым показателем и влияющими на него факторами, используются парные, частные и множественные коэффициенты корреляции, множественный коэффициент детерминации.
Этап 2. Практическая пригодность синтезированной регрессионной модели связи оценивается по величине показателей r (в случае линейности модели), R или R2. Значения всех трех показателей R2, R и r зависят от того, какая типовая форма (8) уравнения регрессии была выбрана, поэтому эти показатели можно рассматривать как измерители степени близостивыбранной теоретической линии регрессии к фактическим данным. Качественный характер такой близости может оцениваться в соответствии со шкалой Чэддока. Индекс корреляции R принимает значения в пределах · близость R к единице означает, что связь между признаками достаточно хорошо описывается избранным уравнением корреляционной зависимости (8); · если R равен или близок к нулю, это означает, что между фактором X и теоретическими значениями признака Y либо нет связи, либо если она и существует, то не может быть охарактеризована выбранным для моделирования типовым аналитическим выражением связи (8). Аналогичные утверждения имеют место и для линейного коэффициента корреляции r, принимающего значения в пределах -1 · близость · близость Пригодность построенной регрессионной модели для практического использования можно оценить и по величине коэффициента детерминации R2 : · неравенство R2 >0,5 позволяет считать, что построенная модель пригодна для практического применения, т.к. в ней достигается высокая степень тесноты связи признаков X и Y, при которой более 50% вариации признака Y объясняется влиянием фактора Х; · неравенство
В тех случаях, когда синтезированы различные (альтернативные) регрессионные модели, коэффициент детерминации R2 используется в качестве критерия предпочтительности того или иного уравнения регрессии: наилучшей считается модель с наибольшим значением R2.
Этап 3. Так как показатели тесноты связи R или r рассчитываются на основе ограниченной совокупности наблюдаемых эмпирических данных (xi, yi), значения которых могли быть искажены влиянием случайных факторов, то найденные по уравнению регрессии показатели тесноты связи r, R проверяются на их неслучайность (значимость).
В начале проверки задается уровень значимости (чаще всего обозначаемый буквой греческого алфавита «альфа» —
Для оценки значимости линейного коэффициента корреляции r применяется t-критерий Стьюдента, фактическое значение которого рассчитывается по формуле:
Расчетное значение критерия tr сравнивается с критическим tтабл, определяемым по таблице значений t-критерия Стьюдента с учетом заданного уровня значимости
Для оценки значимости индекса корреляции R применяется F-критерий ФишераFR, фактическое значение которого определяется по формуле
где m – число параметров уравнения регрессии. Расчетная величина FR сравнивается с критическим табличным значением Fтабл ( Если Fрасч>Fтабл, то величина найденного индекса корреляции R признается значимой. Значимость показателя тесноты связи R или r означает, что зависимость между признаками Х и Y регрессионной модели является статистически существенной, т.е. построенная регрессионная модель в целом адекватна исследуемому процессу. Следовательно, выводы, сделанные на основе регрессионной модели, построенной по данным ограниченной выборки, можно с достаточной вероятностью распространить на всю генеральную совокупность. В качестве критериев адекватности регрессионной модели в практике экономико-статистического анализа, помимо показателя тесноты связи r, R и R2, используются также показатели, оценивающие погрешность модели: · средняя квадратическая ошибка уравнения регрессии
· средняя ошибка аппроксимации
В адекватных моделях ошибки Показатели
5. Экономическая интерпретация построенной регрессионной модели Взаимосвязи признаков Экономическая интерпретация построенной регрессионной модели взаимосвязи признаков – это, по существу, перевод модели с языка статистики и математики на язык экономики. Интерпретация уравнения регрессии используется для целей анализа и прогноза взаимосвязей признаков.
1. В процессе анализа прежде всего выясняются, как факторный признак влияет на величину результативного признака. Чем больше величина коэффициентов регрессии ak при k-ой степени фактора Х, тем значительнее влияние данного признака на результативный. В случае линейного уравнения регрессии Если в соответствии с экономической теорией факторный признак должен иметь положительное значение, а коэффициент ak имеет знак «-», то необходимо проверить расчёты параметров связи, а также возможность ошибок при сборе и обработке информации.
2. С целью расширения возможностей экономического анализа используется коэффициент эластичности 3. Анализируя остатки 4. Уравнение регрессии Прогнозные значения результативного признака Y получают путем подстановки в уравнение регрессии Уравнение позволяет определять в рассматриваемом временном периоде возможные значения признака Y при значениях Х из интервала [ xmin - xmax ].
При прогнозировании значений Y за рассмотренными пределами изменения фактора X необходимо соблюдать следующее ограничение: нельзя подставлять в уравнение регрессии факторные значения xi, существенно отличающиеся от тех, на основе которых это уравнение было получено. Для выполнения этого требования при выборе факторных производных значений х рекомендуется не выходить за пределы 1/3 размаха вариации фактора x (xmax-xmin) как сверх минимального (xmin), так и сверх максимального (xmax)значений, которые имеются в исходных эмпирических данных.
Пример (анализ взаимосвязей с проверкой возможности применения метода КРА).
Имеются следующие данные по отрасли:
Провести на основе приведенных данных исследование взаимосвязи балансовой прибыли и ежегодной суммы амортизации; проверить аналитическое выражение связи на достоверность.
Результативный признак – балансовая прибыль (y); Факторный признак – ежегодная сумма амортизации (х).
Результаты расчетов среднего квадратического отклонения приведены в табл. 1:
Таблица 1.
Среднее квадратическое отклонение:
Коэффициент вариации:
Следовательно, совокупность можно считать однородной.
Для этого определим интервалы для значений признака-фактора:
т.е. (37-4,1)¸(37+4,1); (37-2*4,1)¸(37+2*4,1) и (37-3*4,1)¸(37+3*4,1).
Первичная информация по признаку-фактору не подчиняется закону нормального распределения, однако это не является основанием для отказа использования корреляционно-регрессионного анализа (табл. 2). Таблица 2.
По данным таблицы, резко выделяющихся единиц в первичной информации нет.
Таблица 3.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2017-01-18; просмотров: 1077; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.53.68 (0.174 с.) |

 ) (на рис.3,4 сглаживающие кривые обозначены пунктирной линией).
) (на рис.3,4 сглаживающие кривые обозначены пунктирной линией). (17)
(17) – это средняя величина признака Y, меняющаяся по мере изменения фактора X, а функция f(x) устанавливает аналитический вид однозначной зависимости между вариациями x и
– это средняя величина признака Y, меняющаяся по мере изменения фактора X, а функция f(x) устанавливает аналитический вид однозначной зависимости между вариациями x и 



 для парной регрессии (17) подсказывает график связи Х, Y (рис.5), выполненный на этапе корреляционного анализа.
для парной регрессии (17) подсказывает график связи Х, Y (рис.5), выполненный на этапе корреляционного анализа. для модели связи означает, что выдвигается некоторая гипотеза о типе взаимодействия Х и Y. Так, например, может быть выбрана линейная функция связи или квадратическая, и тогда уравнения регрессии для этих функций будут выглядеть соответственно:
для модели связи означает, что выдвигается некоторая гипотеза о типе взаимодействия Х и Y. Так, например, может быть выбрана линейная функция связи или квадратическая, и тогда уравнения регрессии для этих функций будут выглядеть соответственно: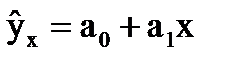 (18)
(18)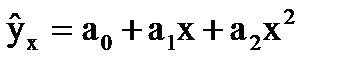 (19)
(19)
 , рассчитанных по избранному для моделирования уравнению регрессии, обусловлен влиянием множества случайных факторов.
, рассчитанных по избранному для моделирования уравнению регрессии, обусловлен влиянием множества случайных факторов. (20)
(20) для всех случаев наблюдения (xi, yi).
для всех случаев наблюдения (xi, yi). min (21)
min (21)

 (22)
(22) ;
;  (23)
(23)
 (24)
(24) = a0 + a1x + а2x2,
= a0 + a1x + а2x2, .
.
 .
.



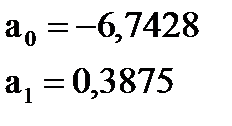


 в построенной модели показывает, что при увеличении стоимости автомобиля на 1000 долларов объём страховых выплат в среднем вырастает на 0,3875 тыс. долларов.
в построенной модели показывает, что при увеличении стоимости автомобиля на 1000 долларов объём страховых выплат в среднем вырастает на 0,3875 тыс. долларов. = f(x1, x2, …, xm)
= f(x1, x2, …, xm) .
. .
. показывают степень влияния каждого фактора на анализируемый показатель при фиксированном (среднем) значении всех других факторов.
показывают степень влияния каждого фактора на анализируемый показатель при фиксированном (среднем) значении всех других факторов. ), оценивающий степень тесноты связи между факторными значениями xi и расчетными результативными значениями
), оценивающий степень тесноты связи между факторными значениями xi и расчетными результативными значениями  ;
; ,
,  ,
,  ,
, ,
, , (25)
, (25) . При этом:
. При этом: r
r  1:
1: к единице свидетельствует о хорошей аппроксимации фактических данных полученной линейной связи
к единице свидетельствует о хорошей аппроксимации фактических данных полученной линейной связи  означает, что построенная модель связи практического значения не имеет ввиду недостаточной тесноты связи между признаками X и Y, при которой менее 50% вариации признака Y объясняется влиянием фактора Х, и, следовательно, фактор Х влияет на вариацию Y в значительно меньшей степени, чем другие (неучтенные в модели) факторы.
означает, что построенная модель связи практического значения не имеет ввиду недостаточной тесноты связи между признаками X и Y, при которой менее 50% вариации признака Y объясняется влиянием фактора Х, и, следовательно, фактор Х влияет на вариацию Y в значительно меньшей степени, чем другие (неучтенные в модели) факторы. ), который показывает вероятность принятия ошибочного решения. Возможность ошибки вытекает из того факта, что для определения взаимосвязи используются данные не всей совокупности, а лишь ее части. Обычно
), который показывает вероятность принятия ошибочного решения. Возможность ошибки вытекает из того факта, что для определения взаимосвязи используются данные не всей совокупности, а лишь ее части. Обычно  .
. , (26)
, (26) ), которое определяется по таблице F- критерия с учетом принятого уровня значимости
), которое определяется по таблице F- критерия с учетом принятого уровня значимости  , представляющая собой среднее квадратическое отклонение эмпирических значений признака Y от теоретических:
, представляющая собой среднее квадратическое отклонение эмпирических значений признака Y от теоретических: (27)
(27) , выраженная в процентах:
, выраженная в процентах: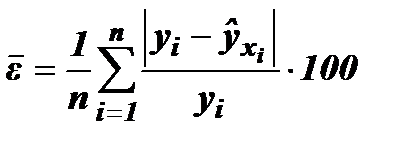 (28)
(28) и
и 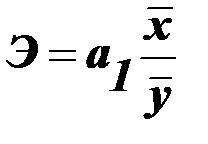 , который показывает, на сколько процентов изменяется в среднем результативный признак при изменении факторного признака на 1%.
, который показывает, на сколько процентов изменяется в среднем результативный признак при изменении факторного признака на 1%. , характеризующие отклонения i -ых наблюдений от значений
, характеризующие отклонения i -ых наблюдений от значений  , которые следует ожидать в среднем, можно сделать ряд практических выводов об эффективности экономической деятельности рассматриваемых хозяйствующих субъектов и выявить скрытые резервы их развития и повышения деловой активности. При этом наиболее значительный экономический интерес представляют наибольшие и наименьшие положительные и отрицательные отклонения
, которые следует ожидать в среднем, можно сделать ряд практических выводов об эффективности экономической деятельности рассматриваемых хозяйствующих субъектов и выявить скрытые резервы их развития и повышения деловой активности. При этом наиболее значительный экономический интерес представляют наибольшие и наименьшие положительные и отрицательные отклонения  .
. может использоваться для краткосрочного прогнозирования ожидаемых значений результативного признака Y в зависимости от тех или иных значений фактора Х.
может использоваться для краткосрочного прогнозирования ожидаемых значений результативного признака Y в зависимости от тех или иных значений фактора Х.

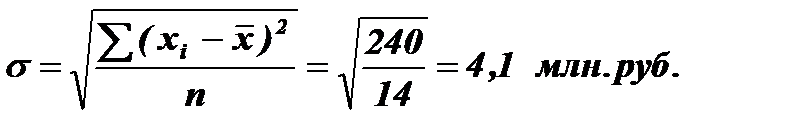

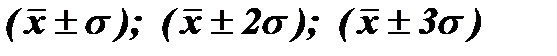 ,
, .
.



