
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика эвольвентного зубчатого зацепления
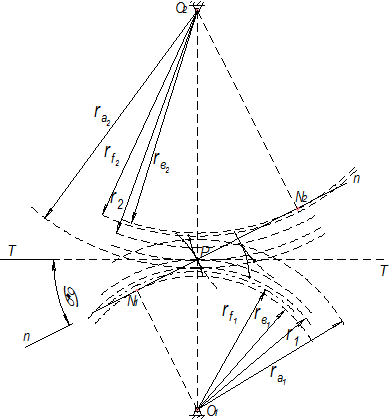 Точки, в которых профили касаются друг друга, называются сопряженными. Так как эвольвентные профили являются взаимоогибаемыми, то в момент касания они имеют общую нормаль. С другой стороны, нормаль к каждому из профилей касательна к основной окружности соответствующего колеса. Следовательно, профили Точки, в которых профили касаются друг друга, называются сопряженными. Так как эвольвентные профили являются взаимоогибаемыми, то в момент касания они имеют общую нормаль. С другой стороны, нормаль к каждому из профилей касательна к основной окружности соответствующего колеса. Следовательно, профили
могут касаться друг друга лишь в те моменты, когда их сопряженные точки приходят на линию Линия так как они совпадают с начальными точками эвольвенты. Поэтому отрезок N1N2 – называют теоретической линией зацепления. Коэффициент перекрытия На рис 2.4 одна и та же пара сопряженных профилей показана в момент начала и конца зацепления. В первом случае ножка ведущего профиля касается крайней точки головки ведомого. Так как касание зубьев возможно лишь на линии произойдет в точке a линии N1-N2, в которой окружность вершин колеса 2 пересекает эту линию. В конце зацепления крайняя точка зуба ведущего колеса 1 касается ножки ведомого колеса. Можно прийти к выводу, что касание зубьев закончится в точке b, в которой окружность вершин колеса 1 пересечет линию зацепления. Отрезок ab линии N1-N2, на котором происходит зацепление двух сопряженных профилей, называют практической линией зацепления.

Используя практическую линию зацепления, легко определить сопряженные точки профилей. Предположим, что нужно найти точку k второго профиля, которая в процессе зацепления будет касаться заданной точки m первого профиля. Касание произойдет в точке
За время зацепления ведущий профиль колеса 1 прошел дугу

где
Скольжение профилей В процессе работы зубчатой передачи профили зубьев не только перекатываются друг по другу, но и скользят. Их скольжение влияет на износ зубьев и тем самым ухудшают качество работы передачи. Для оценки взаимного скольжения профилей зубьев пользуются коэффициентом скольжения, под которым понимается отношение скорости скольжения точек контакта зубьев к касательной составляющей скорости точки контакта сопряженного профиля:

где Практически коэффициенты скольжения вычисляются по следующим формулам.

где g -длина теоретической линии зацепления в миллиметрах; Задаваясь текущей координатой X в пределах от Х=0 до Х=g можно вычислить значения коэффициентов скольжения для обоих колес и построить графики функций.
|
||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 307; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.77.71 (0.008 с.) |
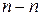 - касательную к обеим основным окружностям. В этот момент нормали к обоим профилям совпадают с данной линией и образуют общую нормаль, проходящую через полюс зацепления
- касательную к обеим основным окружностям. В этот момент нормали к обоим профилям совпадают с данной линией и образуют общую нормаль, проходящую через полюс зацепления  (рис 2.3). В итоге выполняется требование основной теоремы зацепления и колеса передают вращение с заданным передаточным отношением.
(рис 2.3). В итоге выполняется требование основной теоремы зацепления и колеса передают вращение с заданным передаточным отношением. пересечения окружности радиуса О1m с линией зацепления. В эту точку может попасть лишь точка k второго профиля, в которой окружность радиуса О2k пересекает этот профиль.
пересечения окружности радиуса О1m с линией зацепления. В эту точку может попасть лишь точка k второго профиля, в которой окружность радиуса О2k пересекает этот профиль. по делительной окружности и повернулся на угол
по делительной окружности и повернулся на угол  , а ведомый профиль колеса 2 – дугу
, а ведомый профиль колеса 2 – дугу  и повернулся на угол
и повернулся на угол  . Эти дуги называются дугами зацепления. Так как делительные окружности катятся друг по другу без скольжения то дуги зацепления обоих колес будут равными. Если шаг Pw будет больше дуги зацепления, то касание зубьев закончится, а следующая пара зубьев еще не войдет в соприкосновение. В этом случае произойдет перерыв в зацеплении, скорости колес изменятся и следующая пара зубьев войдет в зацепление с ударом. Чтобы этого не случилось, шаг должен быть меньше дуги зацепления, т.е. следующая пара зубьев должна войти в зацепление раньше, чем предыдущая пара выйдет из зацепления. Отношение дуги зацепления к шагу называют коэффициентом перекрытия;
. Эти дуги называются дугами зацепления. Так как делительные окружности катятся друг по другу без скольжения то дуги зацепления обоих колес будут равными. Если шаг Pw будет больше дуги зацепления, то касание зубьев закончится, а следующая пара зубьев еще не войдет в соприкосновение. В этом случае произойдет перерыв в зацеплении, скорости колес изменятся и следующая пара зубьев войдет в зацепление с ударом. Чтобы этого не случилось, шаг должен быть меньше дуги зацепления, т.е. следующая пара зубьев должна войти в зацепление раньше, чем предыдущая пара выйдет из зацепления. Отношение дуги зацепления к шагу называют коэффициентом перекрытия; - шаг зацепления по начальной окружности,
- шаг зацепления по начальной окружности,  – практическая линия зацепления в миллиметрах.
– практическая линия зацепления в миллиметрах.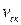 - скорость относительного скольжения профилей;
- скорость относительного скольжения профилей;  и
и  - соответственно тангенциальные составляющие абсолютных скоростей точек профиля.
- соответственно тангенциальные составляющие абсолютных скоростей точек профиля. .- передаточное отношение зубчатого зацепления, для внешнего зацепеления со знаком «минус».
.- передаточное отношение зубчатого зацепления, для внешнего зацепеления со знаком «минус».


