
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрия эвольвентного зацепления
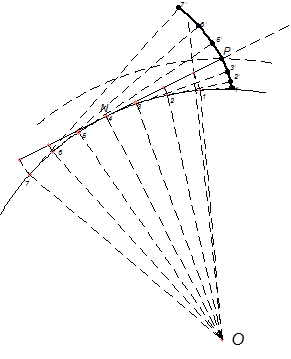
Профили зубьев должны соответствовать основному закону зацепления, который предписывает, чтобы общая нормаль к профилям, проведенная в точке их касания, делила межосевое расстояние на части, обратно пропорциональные угловым скоростям колес. Кроме того, к профилям предъявляется и ряд технологических и эксплуатационных требований: ¾ построение профилей простыми геометрическими методами; ¾ при передаче одинаковой мощности давление на зубья должно быть постоянным по величине и направлению; ¾ простота обработки рабочих поверхностей зубьев; ¾ минимальный износ зубьев; ¾ обеспечение возможности замены одного из колес при их износе и др. Большинству перечисленных требований удовлетворяет профиль, очерченный эвольвентой. В общем случае известно бесконечное множество эвольвент. Для профиля зубьев зубчатых колес используется эвольвента окружности. Эвольвентой окружности называют плоскую кривую, которая описывается любой точкой прямой, перекатываемой по окружности без скольжения. Окружность, по которой перекатывается прямая, называется основной, прямая – производящей прямой. Способ построения эвольвенты вытекает из ее определения. Пусть заданы радиус основной окружности
  б б
Рис 2.2. Построение эвольвенты.
Проведем касательную к окружности, проходящую через точку Положение какой-либо точки эвольвенты
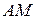 равен дуге равен дуге  или или
 , ,
В формулах (2.9) и (2.10) q - эвольвентный угол, а – угол давления, а + q - угол развертки эвольвенты. Функция (2.10) называется инволютой. Для функций такого типа составлены таблицы, аналогичные таблицам тригонометрических функций. Из прямоугольного треугольника ОАМ находим

Уравнения (2.10) и (2.11) являются параметрическими уравнениями эвольвенты в полярных координатах. Из способа образования эвольвенты следует: ¾ эта кривая не может существовать внутри основной окружности; ¾ она имеет два семейства: левое и правое; ¾ одноименные эвольвенты (правые и левые) эквидистанты, т. е. расстояние между ними, измеренное по общей нормали, одинаково и равно выпрямленным дугам между началами эвольвент.
Из этой формулы следует, что с увеличением угла а, т. е. с удалением от начала эвольвенты, радиус растет, а кривизна
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 247; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.217.228 (0.004 с.) |
 и некоторая точка
и некоторая точка  , расположенная за пределами основной окружности. Требуется построить эвольвенту, проходящую через точку
, расположенная за пределами основной окружности. Требуется построить эвольвенту, проходящую через точку  на несколько равных частей. Далее от точки
на несколько равных частей. Далее от точки  раствором циркуля, равным отрезку
раствором циркуля, равным отрезку  , сделаем четыре засечки на основной окружности. Через полученные точки 0, 1, 2, 3 также проведем касательные. Затем на каждой из касательных откладываем от точек 1, 2, 3 столько отрезков
, сделаем четыре засечки на основной окружности. Через полученные точки 0, 1, 2, 3 также проведем касательные. Затем на каждой из касательных откладываем от точек 1, 2, 3 столько отрезков  (см. рис. 2.2, б) в полярной системе координат задается углом q, отсчитываемый от начального радиус вектора
(см. рис. 2.2, б) в полярной системе координат задается углом q, отсчитываемый от начального радиус вектора  и радиус-вектора
и радиус-вектора  .
.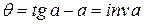

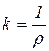 уменьшается, поэтому эвольвента становится менее выпуклой. Из той же формулы видно, что кривизна эвольвенты уменьшается и при увеличении радиуса основной окружности, а при
уменьшается, поэтому эвольвента становится менее выпуклой. Из той же формулы видно, что кривизна эвольвенты уменьшается и при увеличении радиуса основной окружности, а при  эвольвента превращается в прямую линию.
эвольвента превращается в прямую линию.


