
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условие соседства сателлитов
Условие соседства сателлитов необходимо соблюдать при их размещении на водиле. Сателлиты надо размещать таким образом, чтобы при работе они не задевали друг друга головками зубьев (рис. 1.4), то есть должно выполняться неравенство
где
Из чертежа (см.рис.1.5) находим, что
или

Перепишем это равенство в виде
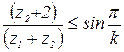
Оно аналитически выражает условие соседства сателлитов.
ПРОЕКТИРОВАНИЕ ЭВОЛЬВЕНТНОГО ЗУБЧАТОГО ЗАЦЕПЛЕНИЯ Общие положения Работу пары цилиндрических зубчатых колес, находящихся в зацеплении, можно представить в виде перекатывающихся без скольжения друг по другу двух цилиндров, называемых начальными. Линии пересечения начальных цилиндров с плоскостью, перпендикулярной осям цилиндров, называют начальными окружностями. Линию пересечения одной из боковых поверхностей зуба с этой же плоскостью называют торцовым профилем зуба. Длина дуги, измеряемая в миллиметрах, между двумя одноименными (левыми или правыми) профилями двух смежных зубьев по какой-либо окружности называется шагом зацепления по этой окружности. Диаметры и радиусы начальных окружностей отмечаются индексом w, а для пронумерованных колес – вместе с индексом ставится номер колеса, например для диаметров -

где z – число зубьев колеса; Pw –шаг зубьев по начальной окружности. Из уравнения (2.1) диаметр начальной окружности выражается иррациональным числом

Для удобства проектирования и изготовления зубчатых колес желательно, чтоб диаметры начальных окружностей выражались рациональными числами в миллиметрах. Из формулы (2.2) следует, что это условие может быть выполнено лишь в том случае, если отношение Отношение величины шага зацепления к числу

тогда Начальная окружность, диаметр которой выражен через стандартный модуль, называется делительной окружностью. Все параметры зубчатого колеса, относящиеся к делительной окружности (радиус, диаметр, шаг и др.), обозначаются без индексов, например r, d, P и т.д.
Основные размеры Нулевого зубчатого колеса На основные размеры элементов зубчатого колеса установлены определенные нормы. Зубчатые колеса, изготовленные по этим нормам, называют нормальными, или нулевыми (выполненными без смещения инструмента), зубчатыми колесами. У нулевых зубчатых колес делительная окружность совпадает с начальной. Рассмотрим сечение нормального зубчатого колеса плоскостью, перпендикулярной к оси вращения (рис 2.1). Все зубья колес одинаковы и расположены по делительной окружности с шагом Р. Часть зуба, выступающая за пределы делительной окружности, называется головкой, а часть зуба, располагающаяся внутри этой окружности, - ножкой. окружность ограничивающая головки зубьев, называется окружностью вершин зубьев.
 Окружность, ограничивающая глубину впадин, называется окружностью впадин. Расстояние между делительной окружностью и окружностью вершин, измеренное по радиусу, называется высотой головки зуба Окружность, ограничивающая глубину впадин, называется окружностью впадин. Расстояние между делительной окружностью и окружностью вершин, измеренное по радиусу, называется высотой головки зуба  . .
Расстояние между делительной окружностью и окружностью впадин называется высотой ножки зуба Для нулевого зубчатого колеса высота головки зуба принимается равной модулю зацепления - Сумма высот головки и ножки

У нулевого зубчатого колеса толщина зуба S и ширина впадины Sb равны половине шага

Для двух зубчатых колес

|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 248; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.36.203 (0.007 с.) |
 ,
, - радиус окружности головок зубьев сателлитов.
- радиус окружности головок зубьев сателлитов.
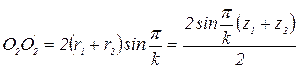
 , для радиусов -
, для радиусов -  .
.
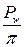 будет рациональным числом.
будет рациональным числом. называется модулем зацепления, то есть
называется модулем зацепления, то есть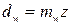 , модули зубчатых зацеплений стандартизированы ГОСТ 9563-60.
, модули зубчатых зацеплений стандартизированы ГОСТ 9563-60. .
. . Высота ножки принимается
. Высота ножки принимается  .
.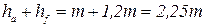 называется высотой зуба. Разность между высотами ножки и головки обозначается как
называется высотой зуба. Разность между высотами ножки и головки обозначается как  и называется радиальным зазором. С учетом принятых величин диаметры окружностей вершин и впадин выразятся как
и называется радиальным зазором. С учетом принятых величин диаметры окружностей вершин и впадин выразятся как
 и
и  находящихся в зацеплении и имеющих один и тот же модуль, определяются межосевое расстояние
находящихся в зацеплении и имеющих один и тот же модуль, определяются межосевое расстояние


