
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для выполнения курсового проектаСтр 1 из 8Следующая ⇒
Методические указания Для выполнения курсового проекта по дисциплине: «Теория механизмов и машин» «Анализ плоского механизма С высшими кинематическими парами» Волгоград ИПК «Нива» УДК 621.01 ББК 34.41 М-54
Методические указания для выполнения курсового проекта по направлению «Теория механизмов и машин» / Сост. Д. С. Гапич. – Волгоградская ГСХА: Волгоград, 2009.-40с
Даны рекомендации по выполнению курсового проекта по дисциплине «Теория механизмов и машин», а также требования к его оформлению. Для студентов факультета механизации сельского хозяйства очной и заочной формы обучения по направлению «Агроинженерия». Рекомендовано методической комиссией факультета механизации сельского хозяйства Волгоградской ГСХА от 13 октября 2009 г., протокол №2.
УДК 621.01 ББК 34.41
Гапич Д.С., 2009 ИПК ФГОУ ВПО ВГСХА «Нива», 2009 ВВЕДЕНИЕ Пособие посвящено рассмотрению одной из основных и наиболее интересных задач курса теории механизмов и машин – задаче синтеза и проектирования зубчатых механизмов. Они использовались человечеством с глубокой древности и в настоящее время находят все большее распространение практически во всех отраслях современного производства. В тракторах и сельскохозяйственных машинах в качестве силовых передач все чаще применяют планетарные механизмы, к которым относят колесные редукторы зерноуборочных комбайнов, бортовые передачи, усилители крутящего момента, редукторы валов отбора мощности тракторов. Данное пособие посвящено исследованию кинематики заданной схемы зубчатого планетарного механизма, а также геометрическому расчету и проектированию простой передачи, состоящей из двух эвольвентных цилиндрических колес внешнего зацепления. Основная цель выполнения первой части листа состоит в определении передаточного отношения механизма и частоты вращения каждого из его ведомых звеньев. При этом необходимо воспользоваться двумя методами: аналитическим и графоаналитическим. Полученные результаты сопоставляются друг с другом. Задача выполнения второй части листа заключается в том, чтобы произвести геометрический расчет размеров всех элементов зацепления и осуществить профилирование (вычерчивание) зубьев пары зубчатых колес для случая, когда зацепление положительное (корригированное).
Изложение теоретического материала в пособии сопровождается рассмотрением конкретных примеров кинематического исследования рассматриваемых схем планетарных механизмов и методика геометрического расчета эвольвентного зубчатого зацепления. ИССЛЕДОВАНИЕ КИНЕМАТИКИ ПЛАНЕТАРНОГО ЗУБЧАТОГО МЕХАНИЗМА 1.1. Основные термины и определения Планетарным называют сложный зубчатый механизм, в котором геометрические оси некоторых зубчатых колес подвижны. Рабочий процесс планетарного механизма рассмотрим на примере редуктора, схема которого представлена на рис. 1.1, а.
а б Рис 1.1. Планетарные механизмы.
Колесо На водиле имеется подшипник, тоже подвижный, в котором вращается вал с закрепленными на нем колесами Колеса
где n – число подвижных звеньев, n =4 (звенья z 1, z 2,
Результат свидетельствует о том, что для обеспечения определенности движения всех звеньев данный механизм должен иметь два ведущих звена. Планетарные механизмы, обладающие двумя и более степенями подвижности, называют дифференциальными механизмами или дифференциалами. Они применяются для привода одного рабочего органа от двух независимых источников энергии или, наоборот, для привода двух рабочих органов с независимыми скоростями от одного источника энергии. Последний вариант применяется для привода ведущих колес автомобиля.
Если в рассматриваемом механизме одно из центральных колес
1.1. Кинематический анализ планетарных передач Цель кинематического исследования планетарного механизма состоит в том, чтобы определить его передаточное отношение, представляющее собой отношение угловой скорости ведущего звена к угловой скорости ведомого звена. Передаточным отношениям приписываются знаки в зависимости от знаков угловых скоростей. Так, например, простой передаче, состоящей из двух зубчатых колес внешнего зацепления, присваивается знак минус, так как колеса вращаются в противоположных направлениях, а передаче с зубчатой парой внутреннего зацепления – знак плюс. Существуют аналитический и графический методы определения передаточных отношений планетарных механизмов. Аналитический, известный как метод Виллиса, более точен и применяется обычно в качестве расчетного. Графический метод имеет меньшую точность и используется в качестве проверочного. Рассмотрим аналитический метод Виллиса. Сообщим мысленно всему планетарному механизму относительно центральной оси (см. рис 1.1) угловую скорость, равную скорости водила и направленную в противоположную сторону, -
где
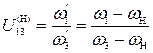
Эта формула связывает между собой скорости вращения центральных колес

Таким образом, передаточное отношение от центрального зубчатого колеса Передаточное отношение планетарной передачи может быть определено и графическим способом, который заключается в построении и использовании картин линейных скоростей. Кинематическая схема механизма при графическом определении передаточного отношения вычерчивается в линейном масштабе (рис 1.2). Справа от схемы механизма проведем вертикальную линию и спроецируем на нее оси колес и полюса зацепления шестерен.
Рис 1.2. Графический способ определения передаточного отношения.
При вращении центрального зубчатого колеса
Ниже проводим горизонтальную прямую Масштаб графика угловых скоростей определится как

Используя масштаб, определяют значения всех остальных оборотов колес.
1.3. Особенности проектирования планетарных передач
 Планетарные передачи выгодно изготовлять с несколькими сателлитами. В этом случае нагрузка на каждую пару зубьев становится меньше, что позволяет сократить ширину зубчатых колес и общие габариты передачи. Планетарные передачи выгодно изготовлять с несколькими сателлитами. В этом случае нагрузка на каждую пару зубьев становится меньше, что позволяет сократить ширину зубчатых колес и общие габариты передачи.
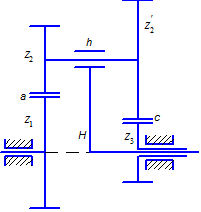
Например, на зерноуборочных комбайнах в качестве колесных редукторов используют однорядную передачу с тремя равномерно размещенными сателлитами (рис 1.3). Однако увеличению числа сателлитов есть определенные ограничения: сателлиты должны размещаться так, чтобы не задевать друг друга головками зубьев (условие соседства); при сборке редуктора сателлиты должны иметь возможность одновременно войти в зацепление с зубьями обоих центральных колес (условие сборки). Есть и другие геометрические ограничения, которые должны учитываться при проектировании планетарных механизмов. Рассмотрим геометрические особенности проектирования планетарных передач на примере однорядного редуктора (передача Джемса), схема которого представлена на рис 1.3.
Условие соосности У всех простых планетарных механизмов оси центральных колес должны располагаться на одной прямой, называемой центральной осью.
Из схемы рис. 1.3 можно записать отношение
или
где Сократив последнее равенство на
откуда

Соотношение (1.11) показывает, что число зубьев сателлита зависит от числа зубьев центральных колес.
Условие сборки редуктора При одном сателлите, если условие соосности выполнено, передача всегда может быть собрана. Однако при числе сателлитов Выразим длину делительной окружности центрального колеса (см. рис 1.3) через шаг
Проделаем то же самое и для центрального колеса:
Длины дуг
где Складывая почленно уравнения (1.12), имеем
Откуда после преобразования, получим
Анализируя это уравнение, заметим, что сумма двух целых чисел
где Переписав полученное равенство в виде
 , ,
получим условие сборки для однорядного редуктора. Его можно сформулировать следующим образом. Чтобы механизм, имеющий
ПРОЕКТИРОВАНИЕ Общие положения Работу пары цилиндрических зубчатых колес, находящихся в зацеплении, можно представить в виде перекатывающихся без скольжения друг по другу двух цилиндров, называемых начальными. Линии пересечения начальных цилиндров с плоскостью, перпендикулярной осям цилиндров, называют начальными окружностями. Линию пересечения одной из боковых поверхностей зуба с этой же плоскостью называют торцовым профилем зуба. Длина дуги, измеряемая в миллиметрах, между двумя одноименными (левыми или правыми) профилями двух смежных зубьев по какой-либо окружности называется шагом зацепления по этой окружности.
Диаметры и радиусы начальных окружностей отмечаются индексом w, а для пронумерованных колес – вместе с индексом ставится номер колеса, например для диаметров -

где z – число зубьев колеса; Pw –шаг зубьев по начальной окружности. Из уравнения (2.1) диаметр начальной окружности выражается иррациональным числом

Для удобства проектирования и изготовления зубчатых колес желательно, чтоб диаметры начальных окружностей выражались рациональными числами в миллиметрах. Из формулы (2.2) следует, что это условие может быть выполнено лишь в том случае, если отношение Отношение величины шага зацепления к числу

тогда Начальная окружность, диаметр которой выражен через стандартный модуль, называется делительной окружностью. Все параметры зубчатого колеса, относящиеся к делительной окружности (радиус, диаметр, шаг и др.), обозначаются без индексов, например r, d, P и т.д.
Основные размеры Нулевого зубчатого колеса На основные размеры элементов зубчатого колеса установлены определенные нормы. Зубчатые колеса, изготовленные по этим нормам, называют нормальными, или нулевыми (выполненными без смещения инструмента), зубчатыми колесами. У нулевых зубчатых колес делительная окружность совпадает с начальной. Рассмотрим сечение нормального зубчатого колеса плоскостью, перпендикулярной к оси вращения (рис 2.1). Все зубья колес одинаковы и расположены по делительной окружности с шагом Р. Часть зуба, выступающая за пределы делительной окружности, называется головкой, а часть зуба, располагающаяся внутри этой окружности, - ножкой. окружность ограничивающая головки зубьев, называется окружностью вершин зубьев.
 Окружность, ограничивающая глубину впадин, называется окружностью впадин. Расстояние между делительной окружностью и окружностью вершин, измеренное по радиусу, называется высотой головки зуба Окружность, ограничивающая глубину впадин, называется окружностью впадин. Расстояние между делительной окружностью и окружностью вершин, измеренное по радиусу, называется высотой головки зуба  . .
Расстояние между делительной окружностью и окружностью впадин называется высотой ножки зуба Для нулевого зубчатого колеса высота головки зуба принимается равной модулю зацепления - Сумма высот головки и ножки

У нулевого зубчатого колеса толщина зуба S и ширина впадины Sb равны половине шага

Для двух зубчатых колес

Коэффициент перекрытия На рис 2.4 одна и та же пара сопряженных профилей показана в момент начала и конца зацепления. В первом случае ножка ведущего профиля касается крайней точки головки ведомого. Так как касание зубьев возможно лишь на линии произойдет в точке a линии N1-N2, в которой окружность вершин колеса 2 пересекает эту линию. В конце зацепления крайняя точка зуба ведущего колеса 1 касается ножки ведомого колеса. Можно прийти к выводу, что касание зубьев закончится в точке b, в которой окружность вершин колеса 1 пересечет линию зацепления. Отрезок ab линии N1-N2, на котором происходит зацепление двух сопряженных профилей, называют практической линией зацепления.

Используя практическую линию зацепления, легко определить сопряженные точки профилей. Предположим, что нужно найти точку k второго профиля, которая в процессе зацепления будет касаться заданной точки m первого профиля. Касание произойдет в точке За время зацепления ведущий профиль колеса 1 прошел дугу

где
Скольжение профилей В процессе работы зубчатой передачи профили зубьев не только перекатываются друг по другу, но и скользят. Их скольжение влияет на износ зубьев и тем самым ухудшают качество работы передачи. Для оценки взаимного скольжения профилей зубьев пользуются коэффициентом скольжения, под которым понимается отношение скорости скольжения точек контакта зубьев к касательной составляющей скорости точки контакта сопряженного профиля:

где Практически коэффициенты скольжения вычисляются по следующим формулам.

где g -длина теоретической линии зацепления в миллиметрах; Задаваясь текущей координатой X в пределах от Х=0 до Х=g можно вычислить значения коэффициентов скольжения для обоих колес и построить графики функций. ПРИМЕР ВЫПОЛНЕНИЯ ПРОЕКТА Порядок выполнения 1. Определяем степень подвижности механизма Число подвижных звеньев
2. Определяем радиусы колес
3. Определяем линейные скорости точек расположенных на ободе первого колеса.
4. Задаемся масштабом плана скоростей.
Картину распределения линейных скоростей точек планетарного механизма строим на вынесенной вправо вертикальной прямой. проецируем на нее оси всех колес и полюса зацепления. Из точки а в принятом масштабе Ниже проводим горизонтальную прямую
Масштаб графика угловых скоростей определится как
Используя масштаб, определяют значения всех остальных оборотов колес. 5. Проводим аналитический расчет Передаточное отношение от первого колеса к третьему определится как где Используя метод Виллиса получим
откуда
Передаточное отношение от первого колеса ко второму
или
откуда
Согласно схеме механизма Передаточное отношение от четвертого колеса к пятому
или
откуда
Согласно схеме механизма Передаточное отношение от шестого колеса к седьмому
Передаточное отношение от седьмого колеса к восьмому
тогда
Используя метод Виллиса получим
откуда
Передаточное отношение от шестого колеса к седьмому
или
откуда
Результаты расчетов сводим в таблицу 1 Таблица 1
Приложения Приложение 1 Таблица значений коэффициента уравнительного смещения Dу при 2³U12>1 по В.Н. Кудрявцеву
Приложение 2 Таблица значений коэффициентов уравнительного смещения Dу и относительного смещения x1 при 5³U12>2 по В.Н. Кудрявцеву
Приложение 3 Таблица значений эвольвентной функции
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 206; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.143.17.127 (0.157 с.) |

 с неподвижной осью вращается вокруг этой оси с угловой скоростью
с неподвижной осью вращается вокруг этой оси с угловой скоростью  . Точно так же колесо
. Точно так же колесо  вращается вокруг неподвижной оси с угловой скоростью
вращается вокруг неподвижной оси с угловой скоростью  . Причем геометрическая ось колес
. Причем геометрическая ось колес  вращается звено, называемое водилом.
вращается звено, называемое водилом. и
и  .
. ,
,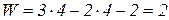

 - угловые скорости звеньев в обращенном движении. То есть при мысленно остановленном водиле планетарный механизм обращается в зубчатую передачу с неподвижными осями колес. Передаточное отношение обращенного механизма выразится формулой Виллиса:
- угловые скорости звеньев в обращенном движении. То есть при мысленно остановленном водиле планетарный механизм обращается в зубчатую передачу с неподвижными осями колес. Передаточное отношение обращенного механизма выразится формулой Виллиса: эта формула примет иной вид. Например, из уравнения (1.2) для механизма (см. рис. 1.2) при
эта формула примет иной вид. Например, из уравнения (1.2) для механизма (см. рис. 1.2) при 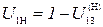
 , где
, где 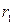 - радиус начальной окружности. Отложим скорость
- радиус начальной окружности. Отложим скорость  от точки
от точки  , расположенной на вертикальной линии
, расположенной на вертикальной линии  , в виде отрезка
, в виде отрезка 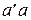 произвольной длины и соединим конец этого вектора (точку a) c проекцией центра точки P. Получим картину распределения скоростей для звена
произвольной длины и соединим конец этого вектора (точку a) c проекцией центра точки P. Получим картину распределения скоростей для звена  , то скорость точки
, то скорость точки  . Рассмотрим зубчатые колеса
. Рассмотрим зубчатые колеса  , поэтому прямая ас – картина распределения скоростей точек для звена
, поэтому прямая ас – картина распределения скоростей точек для звена  , в виде отрезка
, в виде отрезка  . Соединим точку h с точкой P получим картину распределения скоростей точек принадлежащих водилу.
. Соединим точку h с точкой P получим картину распределения скоростей точек принадлежащих водилу.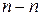 перпендикулярно этой прямой вниз откладываем отрезок 0Р произвольной длины. Из точки Р проводим лучи параллельные соответствующим отрезкам изображающие картины распределения скоростей соответствующих звеньев. Они пересекут прямую
перпендикулярно этой прямой вниз откладываем отрезок 0Р произвольной длины. Из точки Р проводим лучи параллельные соответствующим отрезкам изображающие картины распределения скоростей соответствующих звеньев. Они пересекут прямую 
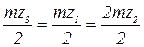
 - модуль зубчатого зацепления (в данной передаче он должен быть общим для внешнего и внутреннего зацепления, так как сателлиты одновременно входят в зацепление с обоими центральными колесами).
- модуль зубчатого зацепления (в данной передаче он должен быть общим для внешнего и внутреннего зацепления, так как сателлиты одновременно входят в зацепление с обоими центральными колесами). , получим
, получим
 одого условия соосности уже недостаточно. Остановимся на этом подробнее. Допустим, что первый сателлит находится с центральными колесами
одого условия соосности уже недостаточно. Остановимся на этом подробнее. Допустим, что первый сателлит находится с центральными колесами  и
и  в зацеплении. Это легко может быть сделано, если сначала ввести сателлит в зацепление с колесом
в зацеплении. Это легко может быть сделано, если сначала ввести сателлит в зацепление с колесом  сателлитов и выполнить условие сборки механизма, необходимо соблюсти определенное соотношение между числом зубьев центральных колес.
сателлитов и выполнить условие сборки механизма, необходимо соблюсти определенное соотношение между числом зубьев центральных колес. и число зубьев
и число зубьев  .
.
 и
и  можно вычислить по формулам
можно вычислить по формулам ;
;  ,
, и
и  - целые числа, а
- целые числа, а  и
и  - отрезки, каждый из которых по величине меньше шага
- отрезки, каждый из которых по величине меньше шага 
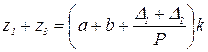
 , будет равна шагу
, будет равна шагу  ,
, - произвольное целое число.
- произвольное целое число. , для радиусов -
, для радиусов -  .
.
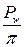 будет рациональным числом.
будет рациональным числом. называется модулем зацепления, то есть
называется модулем зацепления, то есть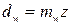 , модули зубчатых зацеплений стандартизированы ГОСТ 9563-60.
, модули зубчатых зацеплений стандартизированы ГОСТ 9563-60. .
. . Высота ножки принимается
. Высота ножки принимается  .
.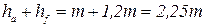 называется высотой зуба. Разность между высотами ножки и головки обозначается как
называется высотой зуба. Разность между высотами ножки и головки обозначается как  и называется радиальным зазором. С учетом принятых величин диаметры окружностей вершин и впадин выразятся как
и называется радиальным зазором. С учетом принятых величин диаметры окружностей вершин и впадин выразятся как
 пересечения окружности радиуса О1m с линией зацепления. В эту точку может попасть лишь точка k второго профиля, в которой окружность радиуса О2k пересекает этот профиль.
пересечения окружности радиуса О1m с линией зацепления. В эту точку может попасть лишь точка k второго профиля, в которой окружность радиуса О2k пересекает этот профиль. по делительной окружности и повернулся на угол
по делительной окружности и повернулся на угол  , а ведомый профиль колеса 2 – дугу
, а ведомый профиль колеса 2 – дугу  и повернулся на угол
и повернулся на угол  . Эти дуги называются дугами зацепления. Так как делительные окружности катятся друг по другу без скольжения то дуги зацепления обоих колес будут равными. Если шаг Pw будет больше дуги зацепления, то касание зубьев закончится, а следующая пара зубьев еще не войдет в соприкосновение. В этом случае произойдет перерыв в зацеплении, скорости колес изменятся и следующая пара зубьев войдет в зацепление с ударом. Чтобы этого не случилось, шаг должен быть меньше дуги зацепления, т.е. следующая пара зубьев должна войти в зацепление раньше, чем предыдущая пара выйдет из зацепления. Отношение дуги зацепления к шагу называют коэффициентом перекрытия;
. Эти дуги называются дугами зацепления. Так как делительные окружности катятся друг по другу без скольжения то дуги зацепления обоих колес будут равными. Если шаг Pw будет больше дуги зацепления, то касание зубьев закончится, а следующая пара зубьев еще не войдет в соприкосновение. В этом случае произойдет перерыв в зацеплении, скорости колес изменятся и следующая пара зубьев войдет в зацепление с ударом. Чтобы этого не случилось, шаг должен быть меньше дуги зацепления, т.е. следующая пара зубьев должна войти в зацепление раньше, чем предыдущая пара выйдет из зацепления. Отношение дуги зацепления к шагу называют коэффициентом перекрытия; - шаг зацепления по начальной окружности,
- шаг зацепления по начальной окружности,  – практическая линия зацепления в миллиметрах.
– практическая линия зацепления в миллиметрах.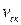 - скорость относительного скольжения профилей;
- скорость относительного скольжения профилей;  и
и  - соответственно тангенциальные составляющие абсолютных скоростей точек профиля.
- соответственно тангенциальные составляющие абсолютных скоростей точек профиля. .- передаточное отношение зубчатого зацепления, для внешнего зацепеления со знаком «минус».
.- передаточное отношение зубчатого зацепления, для внешнего зацепеления со знаком «минус». , число кинематических пар пятого класса
, число кинематических пар пятого класса  , число кинематических пар четвертого класса
, число кинематических пар четвертого класса  .
. -данная передача планетарная.
-данная передача планетарная.


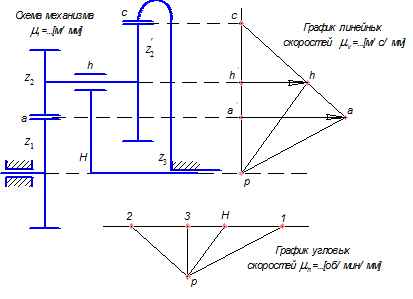
 откладываем влево вектор а-а’. Соединим, точку a’ с точкой O получим картину распределения скоростей точек для первого колеса. Так как третье колесо остановлено, то скорость точки b=0. Соединим точку a’ с точкой b, получим картину распределения скоростей точек для второго и четвертого колеса. Снесем на эту прямую ось вращения второго и четвертого колеса и точку с, получим точку
откладываем влево вектор а-а’. Соединим, точку a’ с точкой O получим картину распределения скоростей точек для первого колеса. Так как третье колесо остановлено, то скорость точки b=0. Соединим точку a’ с точкой b, получим картину распределения скоростей точек для второго и четвертого колеса. Снесем на эту прямую ось вращения второго и четвертого колеса и точку с, получим точку  и с’. Соединим, точку
и с’. Соединим, точку 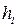 и шестого колеса. Снесем на неё току k принадлежащую шестому колесу, получим точку k’. Рассмотрим пятое и восьмое колесо, скорость точки с известна. Соединим точку с’ с точкой O получим картину распределения скоростей точек для пятого и восьмого колеса. Снесем на эту прямую точку d, получим точку d’. Соединим точку d’ с точкой k’ получим картину распределения скоростей точек для седьмого колеса. Снесем на эту прямую ось вращения седьмого колеса, получим точку
и шестого колеса. Снесем на неё току k принадлежащую шестому колесу, получим точку k’. Рассмотрим пятое и восьмое колесо, скорость точки с известна. Соединим точку с’ с точкой O получим картину распределения скоростей точек для пятого и восьмого колеса. Снесем на эту прямую точку d, получим точку d’. Соединим точку d’ с точкой k’ получим картину распределения скоростей точек для седьмого колеса. Снесем на эту прямую ось вращения седьмого колеса, получим точку  . Соединим, точку
. Соединим, точку  .
.
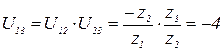
 - передаточное отношение от первого колеса ко второму,
- передаточное отношение от первого колеса ко второму,  - передаточное отношение от второго колеса к третьему.
- передаточное отношение от второго колеса к третьему.



















