
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Оценка надежности уравнения парной линейной регрессии, его параметров и коэффициента парной линейной корреляции
Результаты корреляционно-регрессионного анализа необходимо проверить, проведя оценку существенности, как уравнения регрессии, так и его параметров и коэффициента корреляции. Оценка существенности уравнения регрессии в целом проводится с помощью критерия Фишера – F-критерия. При этом исходят из представления, что если между изучаемыми признаками Для этого вначале проводят исследование дисперсии. Общую сумму квадратов отклонений раскладывают на две части – «факторную» и «остаточную».
где:
Разделив каждую сумму квадратов отклонений на соответствующее число степеней свободы (
Для расчета F-критерия сопоставим факторную и остаточную дисперсию;
Также F-критерий можно рассчитать по формуле:
Оценку существенности уравнения регрессии проводят, сравнивая полученное значение F-критерия ( Если Значимость параметров уравнения Критерий Стьюдента для коэффициента регрессии
где;
Учитывая, что
Критерий Стьюдента для параметра
где:
или Критерий Стьюдента для коэффициента корреляции
или где:
Кроме того, для парной линейной регрессии верно, что:
Полученные фактические значения критерия Стьюдента сравнивают с табличными значениями при определенном уровне значимости
Пример 10. По данным примера 7 и примера 9 провести оценку существенности полученного уравнения регрессии Решение. 1. Оценка статистической значимости функции регрессии проводится при помощи критерия Фишера – F-критерия. Рассчитаем для парной линейной регрессии
Далее фактическое значение 2. Оценка статистической значимости параметров уравнения регрессии Для расчета критерия Стьюдента составим таблицу 26. Таблица 26
Фактически критерий Стьюдента для коэффициента регрессии
Значение стандартных ошибок Фактический критерий Стьюдента для свободного члена уравнение регрессии
Фактически критерий Стьюдента для коэффициента корреляции
Также верно, что Полученные фактические критерии Стьюдента с табличным значением (приложение 1) при определенном уровне значимости и числе степеней свободы Для данного примера табличное значение, при 2) Расчет фактического критерия Фишера и критерия Стьюдента в Microsoft Excel. Фактические значения критериев Фишера и Стьюдента представлены в итоговой таблице, содержащей результаты регрессионного анализа – пример 7, рис. 3. Критерий Фишера расчетный обозначен в столбике F дисперсионного анализа, t-критерии для параметров уравнения Парная нелинейная регрессия
Естественно, что кроме линейных взаимосвязей между явлениями природы, и тем более общественного мира существуют связи нелинейные. Соответственно изучать нелинейные связи при помощи линейной регрессии было бы не верно, для этого необходимо использовать нелинейные регрессии. Но использование нелинейных регрессий связанно следующим ограничением – так как, параметры уравнения регрессии находят при помощи МНК, решая систему нормальных уравнений, а этот метод позволяет оценивать параметры или линейных уравнений или уравнений приводимых к линейному виду, то выбор нелинейных регрессий ограничен – должна существовать возможность линеаризации данных функций. Регрессии, приводимые к линейному виду, подразделяют на два класса: I. нелинейные относительно включенного в модель фактора (независимой переменной), но линейны относительно результата (зависимой переменной). К первому классу относятся такие функции как, например: · полиномы разных степеней;
· равносторонняя гипербола: II. нелинейные относительно включенного в модель результата, но линейны относительно фактора. Ко второму классу относятся такие функции как, например: · степенная функция: · показательная: · экспоненциальная:
Рассмотрим линеаризацию наиболее часто применяемых функций:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-29; просмотров: 467; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.149.168 (0.02 с.) |
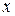 и
и 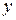 есть связь и уравнение парной линейной регрессии эту связь отражает, то вариация результативного признака
есть связь и уравнение парной линейной регрессии эту связь отражает, то вариация результативного признака  (45)
(45) - общая сумма квадратов отклонений;
- общая сумма квадратов отклонений; - факторная сумма квадратов отклонений;
- факторная сумма квадратов отклонений; - остаточная сумма квадратов отклонений.
- остаточная сумма квадратов отклонений. для общей суммы,
для общей суммы,  для факторной и
для факторной и 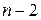 для остаточной) получим дисперсию на одну степень свободы -
для остаточной) получим дисперсию на одну степень свободы -  .
. (46)
(46) (47)
(47) (48)
(48) (49)
(49) (50)
(50) ) с табличным значением (
) с табличным значением ( ), которое берут из таблиц критических значений F-отношений при определенном уровне значимости, как правило:
), которое берут из таблиц критических значений F-отношений при определенном уровне значимости, как правило:  или
или  , и числе свободы:
, и числе свободы:  ,
,  (таблицы Снедекора-Фишера – приложение 2).
(таблицы Снедекора-Фишера – приложение 2). то уравнение регрессии значимо, если меньше незначимо.
то уравнение регрессии значимо, если меньше незначимо. и коэффициента корреляции
и коэффициента корреляции  проверяют при помощи критерия Стьюдента – t-критерия.
проверяют при помощи критерия Стьюдента – t-критерия. рассчитывается как;
рассчитывается как; (51)
(51)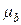 - стандартная ошибка коэффициента регрессии, рассчитывается как:
- стандартная ошибка коэффициента регрессии, рассчитывается как: (52)
(52) (53)
(53) рассчитывается как;
рассчитывается как; (54)
(54) - стандартная ошибка параметра
- стандартная ошибка параметра 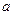 , рассчитывается как:
, рассчитывается как: (55)
(55) (56)
(56)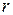 рассчитывается как;
рассчитывается как; (57)
(57) (58)
(58) - стандартная ошибка коэффициента корреляции, рассчитывается как:
- стандартная ошибка коэффициента корреляции, рассчитывается как: (59)
(59)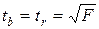 (60)
(60) ,
,  (приложение 1), где
(приложение 1), где 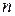 - число единиц наблюдения,
- число единиц наблюдения, 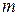 - число параметров уравнения регрессии. Если фактическое значение
- число параметров уравнения регрессии. Если фактическое значение  больше табличного соответствующий коэффициент статистически значим.
больше табличного соответствующий коэффициент статистически значим. , его параметров
, его параметров  ,
,  и коэффициента корреляции
и коэффициента корреляции  .
. . Расчет
. Расчет  проведем по формуле:
проведем по формуле:
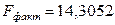 необходимо сравнить с табличным значением. Табличное значение берется из таблиц значения
необходимо сравнить с табличным значением. Табличное значение берется из таблиц значения  Фишера при разных уровнях значимости
Фишера при разных уровнях значимости  (приложение 2). При
(приложение 2). При 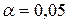 и числе степеней свободы
и числе степеней свободы  ,
,  ,
,  . Так как
. Так как  , можно сказать, что уравнение регрессии статистически значимо.
, можно сказать, что уравнение регрессии статистически значимо. проводится при помощи критерия Стьюдента – t-критерия.
проводится при помощи критерия Стьюдента – t-критерия.


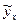

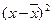
 .
.
 , можно взять из результатов регрессионного анализа в Microsoft Excel – рисунок 3, столбец – стандартная ошибка.
, можно взять из результатов регрессионного анализа в Microsoft Excel – рисунок 3, столбец – стандартная ошибка. .
. .
.

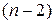 . Если фактические значения t-критерия превышают табличные можно принять, что соответствующее расчетное значение статистически значимо.
. Если фактические значения t-критерия превышают табличные можно принять, что соответствующее расчетное значение статистически значимо. и
и 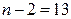 составит
составит  . Все фактические значения t-критерия превышают табличные. Можно сделать вывод о статистической значимости параметров уравнения регрессии
. Все фактические значения t-критерия превышают табличные. Можно сделать вывод о статистической значимости параметров уравнения регрессии  .
. - полином второй степени
- полином второй степени - полином третьей степени и т.д.
- полином третьей степени и т.д. .
. .
. .
. .
.


