
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод Дюамеля щодо розв’язку неоднорідних крайових задач математичної фізикиСодержание книги
Поиск на нашем сайте
Для розв’язку неоднорідної крайової задачі з неоднорідним рівнянням (будь — якого типу) та однорідними граничними й початковими умовами, окрім наведеного методу представлення розв’язку у вигляді ряду за власними функціями, застосовують також метод Дюамеля, який дозволяє звести неоднорідну крайову задачу до відповідної однорідної. Теорема. Якщо функція
то функція
є розв’язком такої неоднорідної крайової задачі:
G 3.5 Приклад розв’язку індивідуального завдання 5 Застосовуючи метод Дюамеля, у півсмузі
де
Розв’язок. Відповідна однорідна крайова задача має вигляд:
де Задачу (3.5.4) — (3.5.6) розв’язуємо методом Фур’є. Її розв’язок шукаємо у вигляді
Згідно з (3.5.4), (3.5.5) та (3.5.7), маємо
Розв’язком наведеної задачі Штурма- Ліувіля (3.5.9) є власні числа
та власні функції
Інтегруючи рівняння (3.5.8) та враховуючи знайдені значення
де Згідно з принципом суперпозиції частинних розв’язків, функція
також задовольняє (3.5.4) та (3.5.5). Знаходимо невідомі
Тоді згідно з (3.5.10), отримуємо остаточний розв’язок допоміжної задачі (3.5.4) – (3.5.6):
Згідно з методом Дюамеля, розв’язок вихідної задачі (3.5.1) — (3.5.3) визначається за формулою
тобто
де
Підставимо (3.5.13) у (3.5.12), отримуємо остаточний розв’язок вихідної задачі
де
? 3.6 Варіанти індивідуального завдання 5 Застосовуючи метод Дюамеля, у півсмузі
Перетворення неоднорідних граничних Умов на однорідні У випадку якщо крайова задача містить неоднорідні граничні умови, то для її розв'язку необхідно перетворити неоднорідні граничні умови на однорідні. Для цього розв’язок крайової задачі шукаємо у вигляді суми:
де одна з функцій, наприклад, Розглянемо деякі окремі випадки граничних умов (2.3.2) і визначимо для них аналітичний вигляд функції Випадок 1 Нехай на кінцях стрижня задані теплові потоки
де Тобто функція
Припустимо:
тоді
Невизначені константи
Покладемо
Випадок 2 а) Якщо на лівому кінці стрижня заданий тепловий потік, а на правому — температура, то для функції
Визначимо функцію
Визначаємо коефіцієнти
Остаточно для функції
б) Якщо на правому кінці стрижня заданий тепловий потік, на лівому — температура, то для функції
Аналогічним способом, відповідно до (3.7.7), (3.7.9), знаходимо:
Випадок 3 Якщо на кінцях стрижня задана температура, то функція
Представляючи функцію
|
||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 321; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.206.141 (0.009 с.) |

 є розв’язком однорідної крайової задачі
є розв’язком однорідної крайової задачі
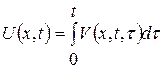

 ,
,  розв’язати крайову задачу з неоднорідним хвильовим рівнянням та однорідними граничними та початковими умовами:
розв’язати крайову задачу з неоднорідним хвильовим рівнянням та однорідними граничними та початковими умовами: ; (3.5.1)
; (3.5.1)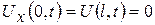 ; (3.5.2)
; (3.5.2) ; (3.5.3)
; (3.5.3)
 ; (3.5.4)
; (3.5.4) ; (3.5.5)
; (3.5.5) , (3.5.6)
, (3.5.6)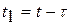 ,
, 
 . (3.5.7)
. (3.5.7) , (3.5.8)
, (3.5.8) (3.5.9)
(3.5.9)
 .
. , отримуємо
, отримуємо ,
, ,
,  — невідомі сталі інтегрування.
— невідомі сталі інтегрування. (3.5.10)
(3.5.10)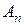 ,
, 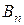 згідно з початковими умовами (3.5.6).
згідно з початковими умовами (3.5.6).

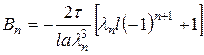 .
. (3.5.11)
(3.5.11)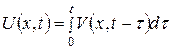 ,
,
 , (3.5.12)
, (3.5.12)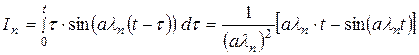 . (3.5.13)
. (3.5.13)
 .
.

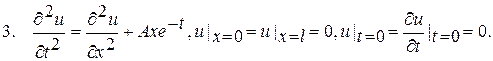





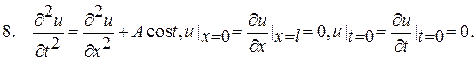
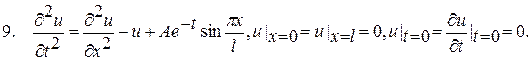
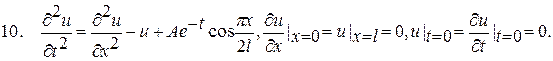


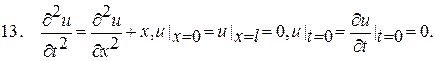

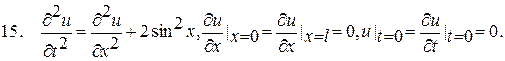





 , (3.7.1)
, (3.7.1)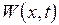 задовольняє задані умови (2.3.2) (із точністю до заміни в них
задовольняє задані умови (2.3.2) (із точністю до заміни в них  на
на  ).
).
 , (3.7.2)
, (3.7.2) ,
,  — відомі функції часу.
— відомі функції часу.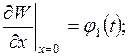
 . (3.7.3)
. (3.7.3) , (3.7.4)
, (3.7.4) .
.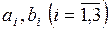 визначаємо з умов (3.4.3)
визначаємо з умов (3.4.3)

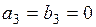 і підставимо отримані значення
і підставимо отримані значення  у вираз (3.7.4), одержуємо таким чином аналітичний вираз для функції
у вираз (3.7.4), одержуємо таким чином аналітичний вираз для функції  , що задовольняє крайові умови (3.7.3):
, що задовольняє крайові умови (3.7.3): (3.7.5)
(3.7.5) (3.7.6)
(3.7.6) у вигляді:
у вигляді: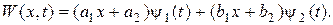 (3.7.7)
(3.7.7) , використовуючи умови (3.7.6):
, використовуючи умови (3.7.6):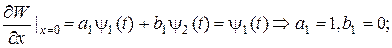


 . (3.7.8)
. (3.7.8) (3.7.9)
(3.7.9) . (3.7.10)
. (3.7.10)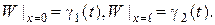 (3.7.11)
(3.7.11) (3.7.12)
(3.7.12)


