
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Та однорідними крайовими умовами
Сформулюємо математичну постановку задачі. Потрібно визначити функцію
задовольняє початкову умову:
і однорідні граничні умови:
(або їхні окремі випадки: формули (2.4.4) — (2.4.6)). Для розв’язку поставленої задачі застосовується метод представлення розв’язку у вигляді ряду за власними функціями відповідної однорідної крайової задачі. Його суть така. Визначаємо власну функцію
Розв’язок вихідної неоднорідної крайової задачі (3.1.1) — (3.1.3) шукаємо у вигляді:
де Представляємо функцію
і знаходимо коефіцієнти цього розкладання:
де Підставляємо розкладання (3.1.5), (3.1.6) у диференціальне рівняння (3.1.1):
Розв’язавши рівняння (3.1.8) звичайними методами (методом варіації довільної сталої, або підстановкою Бернуллі, або методом невизначених коефіцієнтів у випадку спеціальної правої частини) знаходимо:
де Підставляючи вираз (3.1.9) у (3.1.5), одержуємо розв’язок, що задовольняє вихідному рівнянню (3.1.1) і задовольняє задані однорідним граничні умови
Визначаємо сталі Підставивши знайдені значення
G 3.2 Приклад розв’язку індивідуального завдання 4 Застосовуючи метод представлення розв’язку у вигляді ряду за власними функціями, у півсмузі
Розв’язок. Оскільки рівняння (3.2.1) неоднорідне, а граничні умови (3.2.2) однорідні, використовуємо метод представлення розв’язку у вигляді:
де
рішення якої визначається методом Фур'є:
Розв’язком задачі (3.2.5) є функція:
Розкладемо функцію
Підставляючи в (3.2.7) аналітичні вирази для
отримуємо:
Підставивши розклад (3.2.4), (3.2.7) у диференціальне рівняння (3.2.1) одержуємо, відповідно до (3.1.8), диференціальне рівняння для визначення функцій
Функції
Для випадку
Розв'язок рівняння (3.2.11) може бути поданий у вигляді:
де
Отже, відповідно до (3.2.12), знаходимо
Підставляючи отримані вирази для функцій
Визначимо невизначену сталу
отже
Підставляючи знайдене значення
? 3.3 Варіанти індивідуального завдання 4 Застосовуючи метод представлення розв’язку у вигляді ряду за власними функціями, у півсмузі 1.
2.
3.
4. 5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
|
|||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 290; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.67.16 (0.017 с.) |
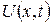 ,
, 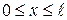 ,
, 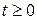 , що задовольняє неоднорідному рівнянню теплопровідності:
, що задовольняє неоднорідному рівнянню теплопровідності: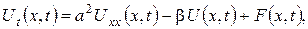 (3.1.1)
(3.1.1)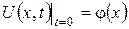 (3.1.2)
(3.1.2)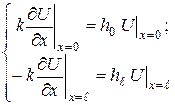 (3.1.3)
(3.1.3) відповідної однорідної крайової задачі (див. п.2.4). У залежності від різновиду граничних умов вона має вигляд:
відповідної однорідної крайової задачі (див. п.2.4). У залежності від різновиду граничних умов вона має вигляд: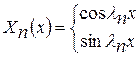 . (3.1.4)
. (3.1.4)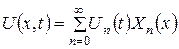 , (3.1.5)
, (3.1.5)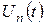 — функції, що необхідно визначити.
— функції, що необхідно визначити.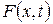 , що входить у диференціальне рівняння (3.1.1), у вигляді:
, що входить у диференціальне рівняння (3.1.1), у вигляді: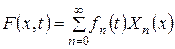 (3.1.6)
(3.1.6)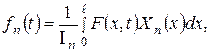 (3.1.7)
(3.1.7)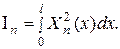
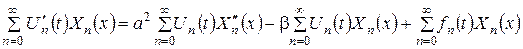 ,
,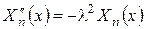 (на підставі (3.1.4)), тому записуючи останній вираз під знаком однієї суми, виносячи загальний множник
(на підставі (3.1.4)), тому записуючи останній вираз під знаком однієї суми, виносячи загальний множник 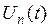 :
: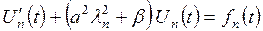 . (3.1.8)
. (3.1.8)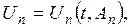 (3.1.9)
(3.1.9)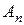 — довільна постійна інтегрування.
— довільна постійна інтегрування.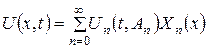 . (3.1.10)
. (3.1.10) ,
,  вирішити наступну крайову задачу:
вирішити наступну крайову задачу: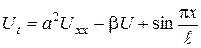 ; (3.2.1)
; (3.2.1)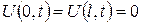 ; (3.2.2)
; (3.2.2)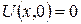 . (3.2.3)
. (3.2.3)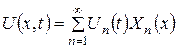 , (3.2.4)
, (3.2.4)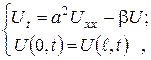
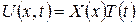 (див. п.2.4), і для функції
(див. п.2.4), і для функції 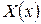 одержуємо таку наведену задачу Штурма-Ліувілля:
одержуємо таку наведену задачу Штурма-Ліувілля: (3.2.5)
(3.2.5)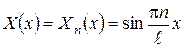 . (3.2.6)
. (3.2.6)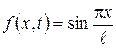 , що входить у диференціальне рівняння (3.2.1), у ряд:
, що входить у диференціальне рівняння (3.2.1), у ряд: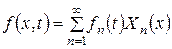 . (3.2.7)
. (3.2.7)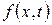 ,
, 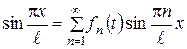 ,
,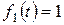 ;
; 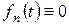
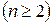 (3.2.8)
(3.2.8)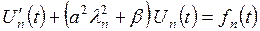 . (3.2.9)
. (3.2.9)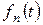 визначаються відповідно до (3.2.8), тому для
визначаються відповідно до (3.2.8), тому для 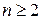 одержуємо однорідне рівняння:
одержуємо однорідне рівняння: 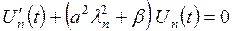 , що має очевидний тривіальний розв’язок:
, що має очевидний тривіальний розв’язок: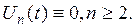 (3.2.10)
(3.2.10)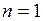 одержуємо відповідно до (3.2.8), (3.2.9) диференціальне рівняння:
одержуємо відповідно до (3.2.8), (3.2.9) диференціальне рівняння: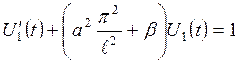 . (3.2.11)
. (3.2.11)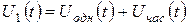 , (3.2.12)
, (3.2.12)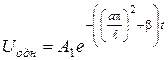 — загальний розв’язок відповідного однорідного рівняння;
— загальний розв’язок відповідного однорідного рівняння; 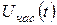 — частинний розв’язок рівняння (3.2.12), обумовлений виглядом правої частини:
— частинний розв’язок рівняння (3.2.12), обумовлений виглядом правої частини: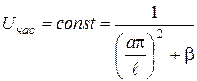 .
.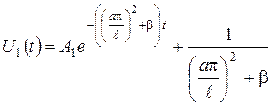 . (3.2.13)
. (3.2.13)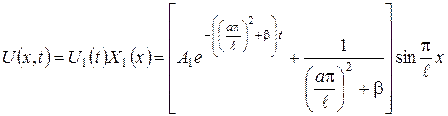 . (3.2.14)
. (3.2.14)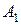 , використовуючи початкову умову (3.2.3):
, використовуючи початкову умову (3.2.3):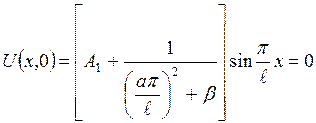 ,
,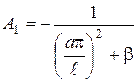 .
.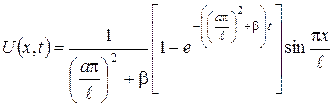 .
.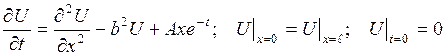 .
.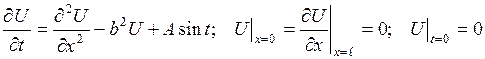 .
.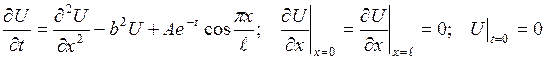 .
.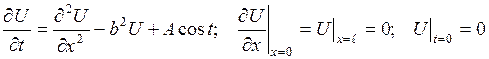 .
.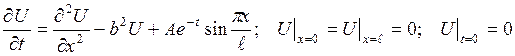 .
.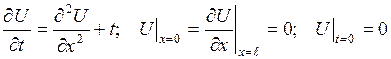 .
. .
.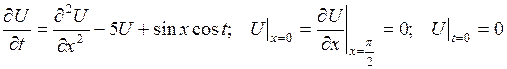 .
. .
.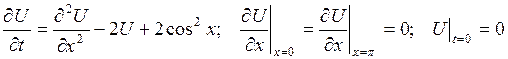 .
.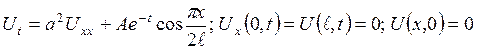 .
.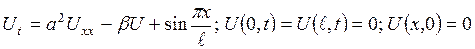 .
.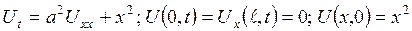 .
.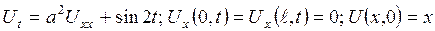 .
.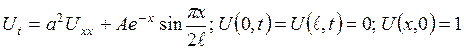 .
.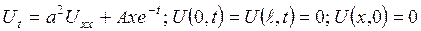 .
.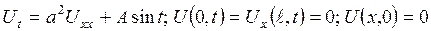 .
.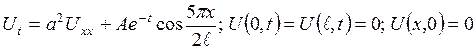 .
.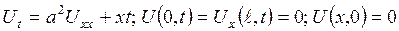 .
.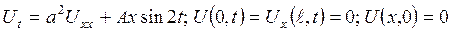 .
.


