
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Для рівнянь параболічного типу
Припустимо, що довжина стрижня дорівнює
задовольняє початкову умову
та однорідні граничні умови
Окремими випадками крайової задачі (2.4.1)-(2.4.3) є задача про визначення функції Задача А: теплоізоляція обох кінців стрижня
Задача Б: сталість температури на кінцях стрижня
Задача В: один із кінців стрижня (наприклад, лівий) теплоізольований, а інший підтримується при постійній температурі
Для розв’язання поставленої однорідної крайової задачі (2.4.1)-(2.4.3) використовується метод поділу змінних — метод Фур'є. Цей метод складається з двох частин. Спочатку знайдемо частинні розв’язки рівняння (2.4.1), що мають вигляд:
Підставляючи вираз (2.4.7) у диференціальне рівняння (2.4.1) і розділивши обидві частини рівності на множник
Ліва частина отриманого рівняння залежить від змінної
або
Загальний розв’язок рівняння (2.4.8) має вигляд:
Оскільки в жодному перетині стрижня (тобто ні при якому фіксованому
Рівняння (2.4.9) набуває вигляду:
Підставимо вираз (2.4.7) у граничні умови (2.4.3), отримуємо:
Функція
Підставляючи в співвідношення (2.4.12) вирази для функції
причому
Розглянемо окремі випадки рівняння (2.4.13). У задачах А, Б, вважаючи відповідно
У задачі В, припускаючи у формулі (2.4.13)
Таким чином, Знайдені значення Таким чином, відповідно до співвідношень (2.4.7), (2.4.10), (2.4.11), розв'язки рівняння (2.4.11), що задовольняють крайові умови (2.4.3), повинні мати вигляд:
де У задачі А
У задачі Б
У задачі В, використовуючи граничні умови (2.4.6), з урахуванням розв’язку (2.4.17) і знайдених значень
У другій частині методу Фур'є за допомогою частинних розв’язків виду (2.4.17) або (2.4.18)-(2.4.20) побудуємо розв’язок, що задовольняє початкову умову (2.4.2). У силу лінійності й однорідності рівняння (2.4.1) сума розв’язків Таким чином, розв’язок задачі (2.4.1) — (2.4.3) може бути поданий у вигляді:
Відповідно до початкової умови (2.4.2):
Система функцій
де Підставляючи знайдені значення
Задача А. Розв’язок згідно (2.4.18) має вигляд:
Згідно з початковою умовою (2.4.2):
знаходимо значення
Підставляючи цей вираз у формулу (2.4.24), одержуємо остаточний розв’язок крайової задачі (2.4.1), (2.4.2), (2.4.4).
Задача Б. Тут розв’язок згідно з (2.4.19) має вигляд:
Початкова умова:
дозволяє визначити значення
і підставивши цей вираз у формулу (2.4.25), отримуємо остаточний розв’язок крайової задачі (2.4.1), (2.4.2), (2.4.5).
Задача В. Розв’язок згідно з (2.4.20) має вигляд:
і початкова умова записується так:
Легко перевірити, що система функцій
Підставляючи вираз (2.4.28) у формулу (2.4.26), одержуємо остаточний розв’язок крайової задачі (2.4.1), (2.4.2), (2.4.6).
|
||||||
|
Последнее изменение этой страницы: 2016-12-30; просмотров: 234; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.221.113 (0.022 с.) |
 . Початок координат на осі
. Початок координат на осі  виберемо на лівому кінці стрижня; тоді його торцеві перетини будуть
виберемо на лівому кінці стрижня; тоді його торцеві перетини будуть  і
і  . Математична постановка однорідної крайової задачі така: необхідно визначити температуру
. Математична постановка однорідної крайової задачі така: необхідно визначити температуру  , що задовольняє однорідному рівнянню
, що задовольняє однорідному рівнянню , (2.4.1)
, (2.4.1) , (2.4.2)
, (2.4.2) (2.4.3)
(2.4.3) . (2.4.4)
. (2.4.4) . (2.4.5)
. (2.4.5) . (2.4.6)
. (2.4.6) . (2.4.7)
. (2.4.7)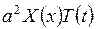 , одержимо:
, одержимо: .
.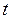 , права — від
, права — від  остання рівність можлива, якщо кожна з частин цього рівняння є константою. Позначимо цю константу «
остання рівність можлива, якщо кожна з частин цього рівняння є константою. Позначимо цю константу « », тоді
», тоді
 , (2.4.8)
, (2.4.8) . (2.4.9)
. (2.4.9) .
. , отже:
, отже: . (2.4.10)
. (2.4.10) і має загальний розв’язок:
і має загальний розв’язок: . (2.4.11)
. (2.4.11)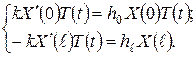

 (у протилежному випадку
(у протилежному випадку  ), тому останні співвідношення можливі у випадку:
), тому останні співвідношення можливі у випадку: (2.4.12)
(2.4.12) згідно з (2.4.11), отримуємо в загальному випадку крайових умов (2.4.3) трансцендентне рівняння для визначення
згідно з (2.4.11), отримуємо в загальному випадку крайових умов (2.4.3) трансцендентне рівняння для визначення 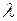 :
: , (2.4.13)
, (2.4.13) . (2.4.14)
. (2.4.14) ;
;  , рівняння (2.4.13) набуває того самого вигляду:
, рівняння (2.4.13) набуває того самого вигляду:  , тоді
, тоді
 (2.4.15)
(2.4.15) , одержуємо тригонометричне рівняння для визначення
, одержуємо тригонометричне рівняння для визначення  , отже:
, отже:
 (2.4.16)
(2.4.16) , отриманих у загальному випадку однорідних крайових умов (2.4.3) із рівняння (2.4.13) або в окремих випадках задач А—В зі співвідношень (2.4.15), (2.4.16).
, отриманих у загальному випадку однорідних крайових умов (2.4.3) із рівняння (2.4.13) або в окремих випадках задач А—В зі співвідношень (2.4.15), (2.4.16). будуть відповідати свої коефіцієнти
будуть відповідати свої коефіцієнти  ,
,  у формулі (2.4.11).
у формулі (2.4.11). , (2.4.17)
, (2.4.17) пов'язані співвідношенням (2.4.14);
пов'язані співвідношенням (2.4.14);  ;
;  ;
;  визначено відповідно до (2.4.13).
визначено відповідно до (2.4.13). . Таким чином, розв’язок задачі А, що задовольняє диференціальному рівнянню (2.4.1) і крайовим умовам (2.4.4) набуває вигляду:
. Таким чином, розв’язок задачі А, що задовольняє диференціальному рівнянню (2.4.1) і крайовим умовам (2.4.4) набуває вигляду: . (2.4.18)
. (2.4.18) . Підставивши (2.4.17) до граничних умов (2.4.5) визначаємо:
. Підставивши (2.4.17) до граничних умов (2.4.5) визначаємо:  . Розв’язок набуває вигляду:
. Розв’язок набуває вигляду: . (2.4.19)
. (2.4.19) . (2.4.20)
. (2.4.20) також буде його розв’язком, і, крім того, задовольнятиме задані крайові умови.
також буде його розв’язком, і, крім того, задовольнятиме задані крайові умови. . (2.4.21)
. (2.4.21) ,
,  . (2.4.22)
. (2.4.22) ,
,  . Згідно з (2.4.22)
. Згідно з (2.4.22)  — коефіцієнти розкладання функції
— коефіцієнти розкладання функції  за ортогональною системою функцій
за ортогональною системою функцій  :
: (2.4.23)
(2.4.23) .
. . (2.4.24)
. (2.4.24)
 — коефіцієнтів розкладу функції
— коефіцієнтів розкладу функції  .
. . (2.4.25)
. (2.4.25)

 , (2.4.26)
, (2.4.26) ,
, 
 ортогональна на інтервалі
ортогональна на інтервалі  , тому коефіцієнти
, тому коефіцієнти  (2.4.28)
(2.4.28)


